Matematiği eğlenceli yapan ve bazen de kafa karışıklığına sebep olan paradokslar ilginç ve bir o kadar da macera doludur. İnsan bu paradoksları bir yandan çözüme kavuşturmaya çalışırken sonunda bir mantık hatasına düşer ya da sürüklenir. Eski Yunan matematiğinde de bazı paradokslar karşımıza çıkar. Genellemenin önemli olduğunu bilsek de bazı durumlar da yapılan genellemeler bizi tehlikeye düşürebilir. Dikkat etmemiz gerek!
Tahmini MÖ 5. yy ‘ da Zenon sonsuzluk, diziler ve kısmi toplamlar ile ilgili bilgilerini kullanarak ünlü bir paradoks geliştirmiştir. Zenon, Aşil ve kaplumbağa arasındaki yarışta kaplumbağanın yarışa 1000 metre önden başlamasını önerir. Aşil’in kaplumbağadan 10 kat daha hızlı koşabildiğini varsayın. Yarış başladığında ve Aşil 1000 metre ilerlediğinde, kaplumbağa Aşil’in 100 metre önünde olacak. Aşil, daha sonraki 100 metreyi aştığında kaplumbağa 10 metre ileride olacak.
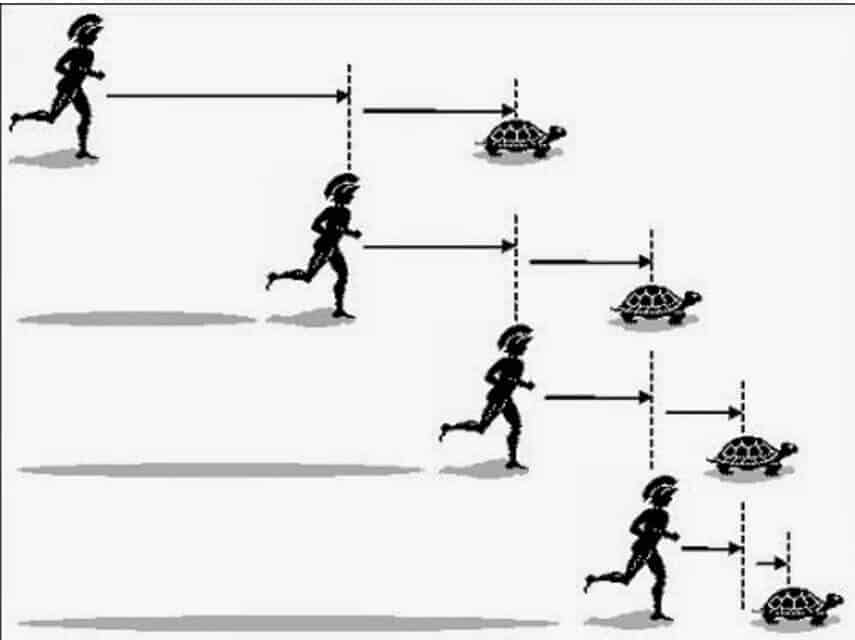Zenon’a göre Aşil sürekli olarak kaplumbağaya yaklaşacak; ama ona hiçbir zaman yetişemeyecek. Zenon’un sizce düşüncesi doğru mu? Eğer Aşil kaplumbağayı geçecek olsa, bu yarışın hangi noktasında olabilir? Çözümü ileride vereceğim!
Euclid ve Zenon paradoksları olarak da bilinen birkaç paradoks mevcuttur. Eski Yunanlı düşünür Euclid hiçbir zaman bir kum yığını oluşturulamayacağını öne sürmüştür. Doğal olarak, bir kum tanesi bir kum tepesi olarak ele alınamaz. Eğer bir kum tanesine bir tane daha eklersek bunlar da bir yığın oluşturmaz. Bu nedenle eğer kum yığınınız yoksa ve elinizde olana bir ekleyerek bir yığınınız olmuyorsa o zaman hiçbir zaman hiçbir bir kum yığınınız olamayacak.
Benzer şekilde bir akıl yürütme ile Zenon bir doğru parçasının üzerindeki noktalara bakar. Zenon’a göre eğer bir noktanın boyutu yoksa o zaman bir noktaya bir nokta daha eklendiğinde bunun da boyutu olmayacaktır. Bu nedenle noktalar birleşerek herhangi bir boyutu olan bir nesne ya da şekil elde edemeyeceğiz. Ama eğer bir noktanın boyutu olsaydı, o zaman bir doğru parçası sonsuz uzunlukta olurdu çünkü içinde sonsuz sayıda doğru vardır.
Kim haklı sizce?