Merhaba arkadaşlar bu yazımızda sizlere zaman mekan ilişkisi ve bölerek deneme algoritmasını anlatacağım. Öğrendim ki Nasa mühendisleri Mars gezegeninde kullanacakları bellek platformu curiosity ile aynı olacakmış. Curiosity iki bilgisayar ile donatılmıştı. Fakat aynı anda sadece 1 i aktif halde bulunabiliyordu.
Curiosity bilgisayarlarının özelikleri şöyle idi:
- 2 gb flash bellek.
- 256 mg rastgele erişimli bellek.
- Temel sistem işlevlerinin barındıran 256 kb salt okunur bellek.

Tüm bir programı RAM’e yerleştirebilmek istiyoruz. Ne var ki alanı diğer programlarla paylaşmak zorunda olduğumuz için RAM’in sadece yüzde 5’i bize ayrılmış. Yani en fazla yüzde 5 ini kullanabiliyoruz. Buda toplamda yaklaşık 12,8 mg eder.
Bu konuyu açtım çünkü size zaman mekan takası ( Zaman Mekan İlişkisi) kavramından bahsetmek istiyorum veya mekan zaman takası. Bilgisayar terimlerinde bu terim çok kullanılır.
Öncelikle Bölerek Deneme Algoritması örneği görelim. Aşağıda ki gif te görüldüğü gibi ilk olarak 2 den başlamak suretiyle sayıları bölmeye başlıyor. Ardından 3,5,7 diye ilerliyor. Bu sayılardan hiç birine bölünmeyen sayıları asal sayı olarak kabul ediyor.
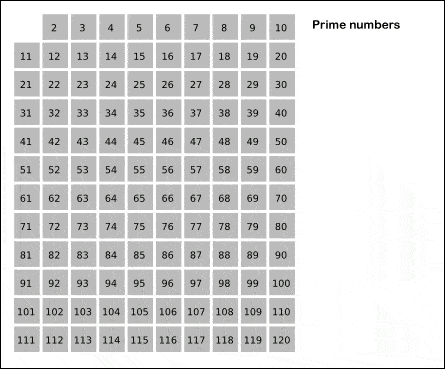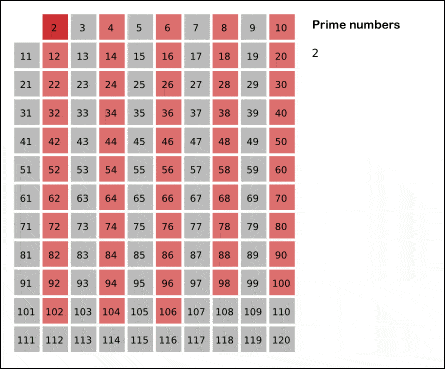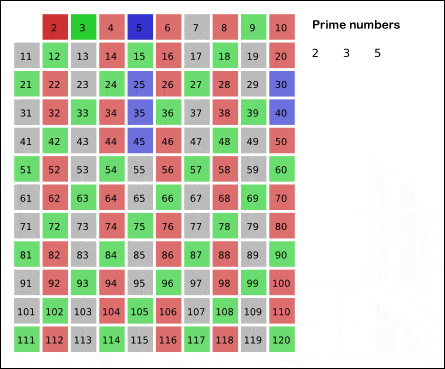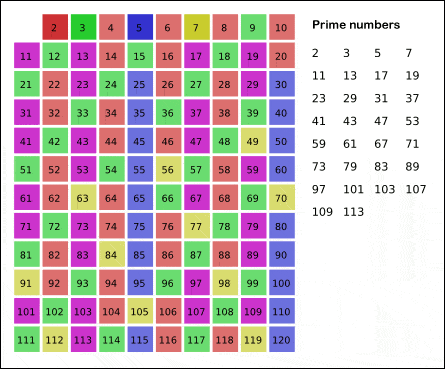
Bu yönteme Eratosthenes Kalburu yöntemi deniliyor. Sizler için bunun programını yazıp sitemize ekledik. Yalnız çok fazla ram tükettiğinden genişlik 600 den sonrası için hesaplayamıyor tarayıcınız donabilir.
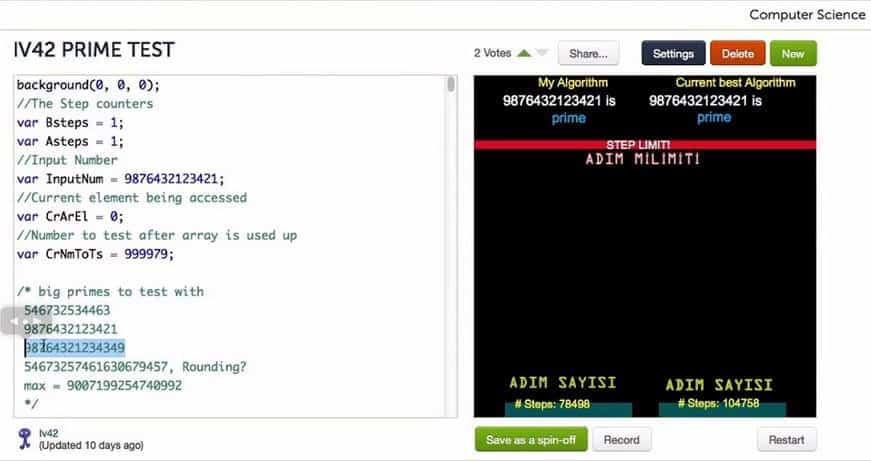
IV 42 tarafından yazılan bi programa bakalım. Bir milyondan asaldan oluşan bir dizi kullanılmış olsun, böylece algoritması bölerek deneme asallık testini uygularken mümkün olduğu sürece yalnızca asallara bakarak ilerliyor. Şöyle de bir soru sormuş kendisi, o anda hesaplamaya çalışmak yerine belli bir sınıra kadar ihtiyacımız olan tüm asaları niçin bir dizide saklamıyoruz?
Aslında bunun cevabı bölerek denerek algoritması için en iyi yöntemdir. Bu algoritma çok fazla adım kullanmıyor olsa da daha adım limitine ulaşamadan çok fena şekilde yavaşlayıp ve sonunda gelmeden kitlenip kalacaktır. MAX=9007199254740992
Yani daha önce tanımladığımız bu boyut için problemi hızlı bir şekilde çözmeyi başarmadı. Bu örnekte tekrar tekrar bölünebilirlik testi yapmadan zamandan tasarruf edecek karşılığında ise mekandan, yani dizinin yerleştiği bellekten taviz verecekti. Peki neden işe yaramadı ?
Şimdi öğrendiklerimizi kullanarak kaba bir hesap yapalım. Ve bellek sınırlarımız dahilinde bu yöntemi kullanabileceğimizin mümkün olup olmadığına bakalım.
Hatırlayalım; 9 kat trilyon biraz üstünde ki sayılara işlem yapabilmemiz gerekiyor. Bölerek deneme algoritmamız sadece sayının kareköküne kadar sayıları denemeli. O noktaya kadar hiç çarpan bulamadı ise sayının asal olup olmadığını kesin bir şekilde söyleyebilmeli, şimdi bu sayının kareköküne ulaşarak kaç asal sayı geçmemiz lazım?
√9007199254740992= 94. 9 milyon olduğunu belirteyim.
Şimdi 95 milyondan küçük kaç asal sayı var?
Neysekı bu soruya yaklaşık bir cevap verebilmemizi sağlayan matematiksel bir çözüm biliyoruz.
Asal Sayı Teoremi
O halde x den küçük kaç asal sayı vardır? x bölu x in dogal logaritması kadar. x 94,9 milyondan biraz büyük sayı oldugunda asal sayıların sayısı yaklaşık 5.1 milyon olur. Şimdi bu asal sayıları saklayamayacağımıza gore en buyuk asalın yanı bu durumda yaklaşık 5166823. asal sayının boyutunu bilmek gerekir ki bu sayınınn 94.9 milyondan küçük olacağını biliyoruz
İşlemlerden sonra en büyük asal sayı 89078611 çıktı. Peki yalnız bu asal sayıyı saklamak için ne kadar belleğe ihtiyacımız var ? Bunu bulmak için sayıyı 2 lik sisteme dönüştürelim. Çünkü bilgisayarlar sayıyı bu şekilde saklar.
En büyük asal sayıyı bit şeklinde yazınca;
89078611=100001111110110001010101 Burada 24 bit var. Yani tek bir sayıyı saklamak için 3 byte gerekiyor.
Şimdi diyelim ki tüm sayıları bellekte saklamak istiyoruz. En buyuk sayı 24 bit gerektirdiğine göre her asal sayı için 24 er bitlik bloklardan oluşan uzun bir liste düşünebiliriz. Listenin tamamı için kaç bit gerekir ?
Gereken Bellek=Değer x Alan
5166822 x 24 = 124003728 Bit = 14,7 Megabayt
Nerede ise 15 mg. Demek ki sınırlarımız dahilinde bu sayılardan oluşan listeyi bile bellekte saklamamız mümkün değil. Bunu söylediğimize göre artık bunu biliyoruz. Nispeten küçük bu sayının kare köküne kadar olan sayıları saklamak bu bellek sınırları dahilinde mümkün değil. Bu şekilde yapamıyoruz. Peki ya ödediğimiz bedel bin kata hatta 10 bin kat düşerse. Modern kriptografik sistemlerde 512 bit hatta daha büyük boyutlar kullanılır. Böylece arama ve sayma imkansız halde geliyor. Mesela biri sizden 200 basamağa kadar olan tüm asal sayıların listesini isterse bunu aklınızdan bile geçirmemelisiniz.
Çünkü bunu saklayabilecek sabit diskin kütlesi gözlemlenebilir evrenden daha büyüktür. Hesabı yapmayı size bırakıyorum. Ama şunu bilin ki gözlemlenebilir evrende 10 üzere 80 atom bulunuyor. Bu 80 haneli bir sayı. Şimdi erişimimizi olan alan veya belleğin temel bir sınır var. Problemlerimizi çözerken mekan ve zaman kullanımları arasında daima bir çekişme vardır. O halde bu asallık problemi testini küçük bir alan ve az bir zaman kullanarak hızla çözmek için ona bambaşka bir açıdan yaklaşmamız gerek.