Yüzey İntegralleri

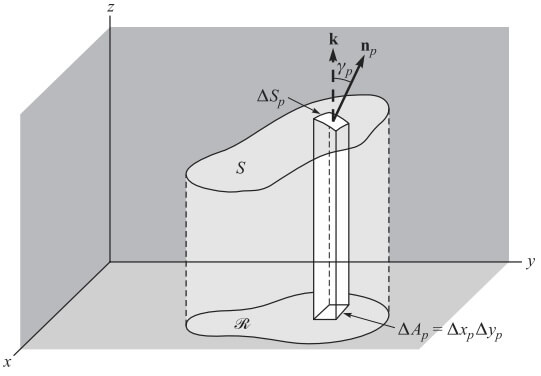
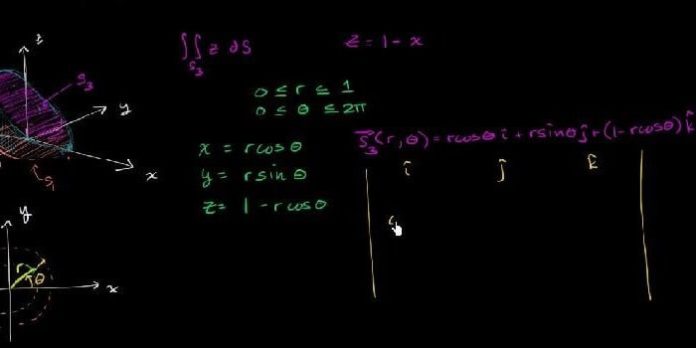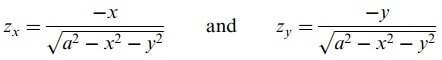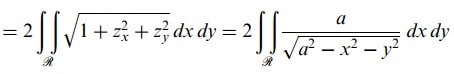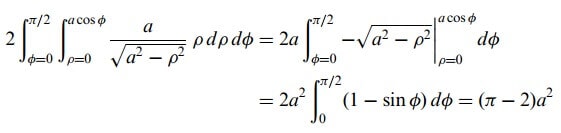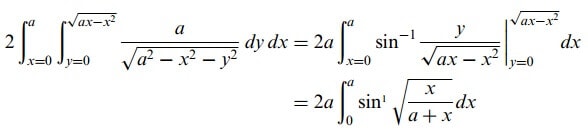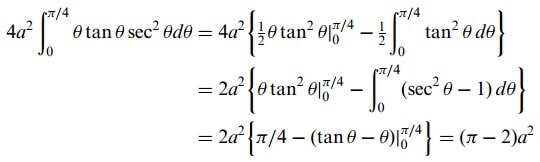Merhaba arkadaşlar bu yazımızda sizlere yüzey integralleri ve konuyu daha iyi kavramanız için yüzey integralleri ile ilgili örnek çözeceğim. S yandaki Şekil 1’de görüldüğü gibi xy düzleminde R dik izdüşümüne sahip iki yanlı bir yüzey olsun. f  R deki her x ve y için tek değerli ve sürekli olmak üzere S için bir denklem z =(x,y) olsun. R yi ΔA_p, p=1,2,…,n  alanına sahip n alt bölgeye ayırınız ve bu alt bölgelerin her biri üzerinde S yi ΔS_p alanıyla kesen düşey kolonlar dikiniz.

Φ(x, y, z)  S’nin tüm noktalarında tek değerli ve sürekli olsun. (ξ_p, η_p, ℑ_p) ΔSp’nin bir noktası olmak üzere

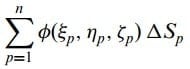
toplamını oluşturunuz. Eğer bu toplamın n––>∞ iken her bir ΔS_p––>0 olacak şekilde bir limiti varsa, limitin değeri Φ(x, y, z) nin S üzerinde yüzey integralleri olarak adlandırılır ve

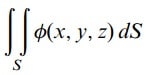
ile gösterilir.

γ_p S’nin normaliyle pozitif z ekseni arasındaki açı olmak üzere yaklaşık olarak ΔS_p = lsecγ_pl olduğundan, (eşitlik 1) toplamının limiti

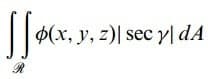
yazılabilir. lsecγ_pl büyüklüğü

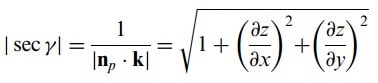
ile verilir. Bu taktirde, R de z = f(x, y) sürekli(veya parçalı sürekli) türevlere sahip kabul edilerek (eşitlik 3) dik koordinatlarda

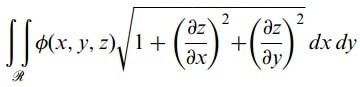
şeklinde yazılabilir.

S için denklemin F(x, y, z) = 0 olarak verilmesi halinde,

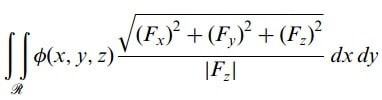
olur. (eşitlik 5) veya (eşitlik 6) sonucu (eşitlik 2) ‘in değerini bulmak için kullanılabilir.

Yukarıda S’yi z eksenine paralel bir doğruyla sadece bir noktada kesişiyor kabul ettik. S’nin böyle olmaması halinde, çoğunlukla S’yi bu tipteki S1, S2,…, yüzeylerine böleriz. O zaman S üzerinde yüzey integralleri S1, S2,…, üzerinde yüzey integrallerinin toplamı olarak tanımlanır.

Yukarıda ifade edilen sonuçlar S xy düzleminin bir R bölgesine izdüşürüldüğü zaman geçerlidir. Bazı hallerde S’nin yz veya xz düzlemlerine izdüşürülmesi daha iyidir. Böyle hallerde (eşitlik 2) ifadesi, (eşitlik 5) ve (eşitlik 6) uygun şekilde değiştirilerek hesaplanabilir.

Yüzey İntegralleri İle İlgi Örnek

a yarıçaplı bir yarı küre çapı 0 olan bir silindir tarafından kesilmiştir(oyulmuştur). Oluşan yüzeyin alanını bulunuz.

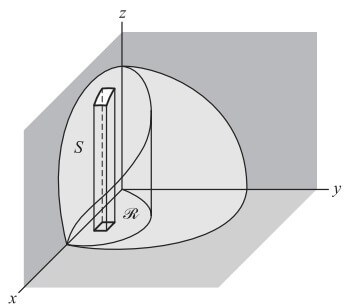
Yarıkürenin ve silindirin(şekil 2) denklemleri sırasıyla X² + y² + z² = a² (veya z = (a² – x² – y²)^1/2) ve (x – a/2)² + y² = a²/4 (veya x² + y² = ax) tir.

olduğundan istenilen alan;

olarak bulunur. İntegralin hesaplanması için iki metodun uygulanması mümkündür.

1.metod: Kutupsal koordinatların kullanılması x2 + y2 = ax kutupsal koordinatlarda ρ=acosΦ

olduğundan, integral

şekline gelir.

2.metod: İntegral

‘ ye eşittir x = atan²Θ denirse, bu integral

haline gelir. Size bugün yüzey integralleri anlattım. Bu konumuzun devamı olan stokes teoremi ve diverjans teoremi yazılarımızda görüşmek üzere.