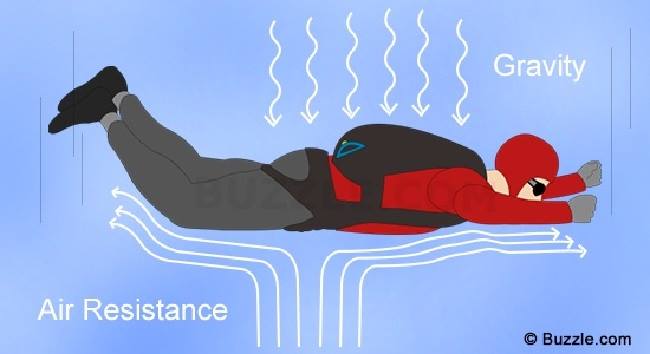
Bu yazımda yüksek hızlarda hava direnci başlığı altında olacak. Hava içerisinde çok büyük hızla hareket eden ve büyük boyutlu cisimler, örneğin uçaklar, hava dalgıçları, beysbol topu gibi cisimler için direnç kuvveti yaklaşık olarak hızın karesi ile orantılıdır. Bu durumda direnç kuvveti aşağıdaki gibi ifade edilebilir:
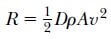
Burada ρ havanın yoğunluğu; A düşen cismin hareketine dik doğrultudaki yüzeyine karşı gelen alandır. D direnç katsayısı olarak adlandırılan boyutsuz bir katsayıdır. Bu direnç katsayısı küresel cisimler için yaklaşık olarak 0,5 değerine sahiptir. Fakat düzensiz şekilli cisimler için 2 değerine kadar yükselir.
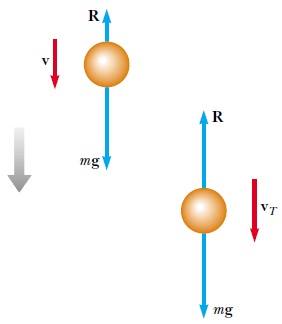
Şimdi yukarı doğru R = 1/2DρAv2 ile verilen hava direnci etkisinde serbest düşme yapan bir kütlenin hareketini inceleyelim. Bir w kütleli cisim Şekil 6.16 da görüldüğü gibi y = 0 konumunda durgun halden serbest bırakılsın. Kütle iki dış kuvvet etkisinde kalır. Bunlar aşağı doğru olan Fg = mg çekim kuvveti ve yukarıya yönelmiş olan R direnç kuvvetidir. Ayrıca ihmal ettiğimiz yukarı doğru yönelmiş bir de kaldırma küveti vardır. Böylece etki eden net kuvvetin büyüklüğü aşağıdaki gibidir:
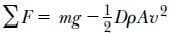
Burada aşağı yönü pozitif aldık Fnet = ma ifadesini (6.7) Eşitliğinde yerine koyarak kütlenin aşağı yönlü ivmesinin büyüklüğünü buluruz:
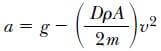
Limit hız ifadesini, direnç kuvvetinin ağırlığa eşit ve ivmenin sıfır olmasından aşağıdaki gibi elde ederiz. Eşitlik (6.8) de a= 0 konularak ve v yi de vi alarak
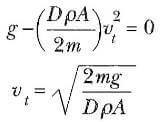
bulunur. Bu ifadeyi kullanarak limit hızın, cismin boyutlarına nasıl bağlı olduğunu belirleyebiliriz. Cismin r yarıçaplı bir küre olduğunu varsayalım. Bu durumda A ∞ r (A= πr2 den) ve m ∞ r3 dür (kütle hacimle orantılı olduğu için çünkü V=4/3 πr3 dir). Böylece vt∞√r olur. Yani r arttıkça vt hızı, yarıçapın karekökü ile orantılı olarak artacaktır.
Tablo 6.1 de, hava içinde serbest düşme yapan çeşitli cisimlerin limit hızları liste halinde verilmiştir.