Merhaba arkadaşlar bu yazımızda sizlere vektörlerin özelliklerini anlatacağız, bunun yanı sıra konuyu daha iyi kavramamız için vektörlerin özellikleri ile ilgili örnek çözeceğiz.
İki Vektörün Eşitliği
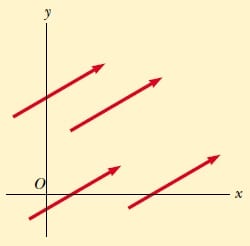
Birçok amaç için, A ve B gibi iki vektör aynı büyüklüğe ve aynı yöne sahipse eşit alınabilir. Yani, A = B ise ve paralel doğrular boyunca aynı yönü gösteriyorlarsa A = B ’dir.
Örneğin Şekil 1’deki bütün vektörlerin başlangıç noktalan farklı olmasına rağmen eşittirler. Bu özellik, vektörü etkilemeden, bir vektörü kendisine parelel olarak öteleme hareketi yaptırmamıza izin verir.
Vektörlerin Toplanması
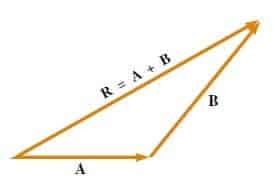
Vektörlerin toplanma kuralları, geometrik yöntemlere uygun olarak tanımlanır. B vektörünü A vektörüyle toplamak için, önce grafik kağıdı üzerine, büyüklüğü uygun bir ölçek ile temsil edilen A vektörü çizilir ve sonra B vektörü Şekil 2’deki gibi, başlangıcı A nın ucundan başlayarak aynı ölçekte çizilir. R = A + B bileşke vektörü, A nın başlangıcından B nin ucuna çizilen vektördür. Bu işlem, toplamanın üçgen yöntemi olarak bilinir.
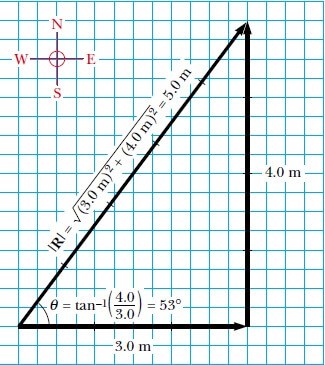
Örnek olarak, Şekil 3’de gösterildiği gibi 3,0 m doğuya, daha sonra 4,0m kuzeye doğru yürürseniz, kendinizi başladığınız yerden 53° kuzey-doğuya 5,0 m uzaklaşmış bulursunuz.
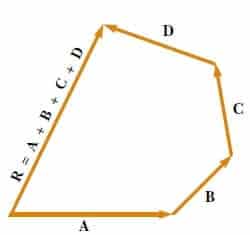
Geometrik çizimler, iki vektörden daha fazlasını toplamak için de kullanılabilir. Dört vektör hali Şekil 4′ de gösterilmektedir. Bileşke vektör, R = A + B + C + B çokgeni tamamlayan vektördür. Başka bir deyişle R birinci vektörün başlangıcından son veklörün ucuna çizilen vektördür.
İki vektörün toplanması için, toplamada paralel kenar kuralı olarak bilinen, değişik bir grafik işlem, Şekil 5a’ da gösterilmiştir. Bu çizimde, iki A ve B vektörünün başlangıçları aynı noktadadır ve bileşke R vektörü; kenarları A ve B ile oluşan bir paralel kenarın köşegenidir.
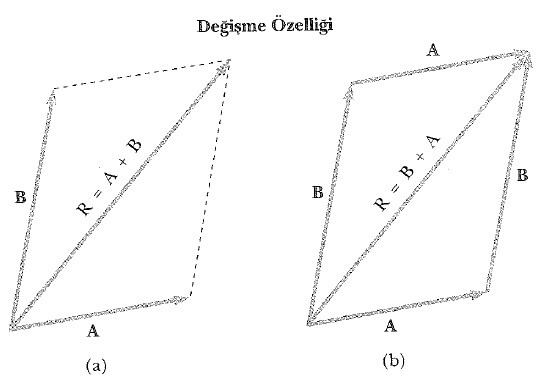
İki vektör toplandığında sonuç, toplamın sırasından bağımsızdır. (Bunu deneyerek görebilirsiniz, vektörler çarpılırken sırası önemli olur.) Bu, Şekil 5b’ deki geometrik çizimden görülebilir ve toplamanın değişme özelliği olarak bilinir:
A + B = B + A (Eşitlik 1)
Üç veya daha fazla vektör toplanırken; sonuç, vektörlerin birbirleriyle gruplandırılma şeklinden bağımsızdır. Üç vektör için geometrik ispat. Şekil 6′ da verilmektedir. Buna toplamanın birleşme özelliği denir:
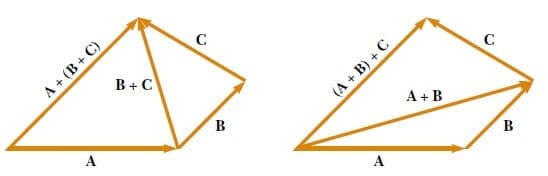
A + (B + С) = (A + В) + С (Eşitlik 2)
Özelle, bir vektöre! nicelik, hem büyüklüğe hem de yöne sahip olan ve Şekil 2 den Şekil 6’ya kadar olan çizimlerde belirtildiği gibi vektörel toplama kurallarına da uyan bir niceliktir.
Bir Vektörün Negatifi
A vektörünün negatifi, A vektörüyle toplandığı zaman sonucu sıfır eden vektör olarak tanımlanır. Yani, A + (-A) = 0. Bu A ve -A vektörleri aynı büyüklükle fakat zıt yönlüdürler.
Vektörlerin Çıkarılması
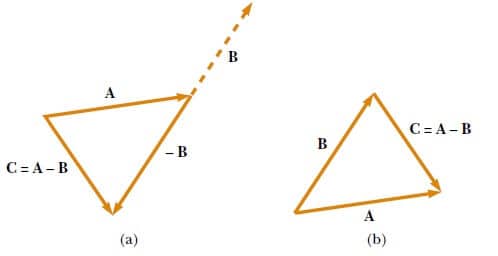
Vektörlerin çıkarma işleminde, bir vektörün negatifinin tanımından yararlanılır. A – В işlemini, A vektörü ile toplanan -B vektörü olarak tanımlarız:
A-B = A + (-B) (Eşitlik 3)
İki vektörün çıkarılması ile ilgili geometrik çizim Şekil 7′ da gösterilmiştir.
Vektörlerin çıkarma işlemine başka bir şekilde de bakılabilir: A ve В gibi iki vektörün A-B farkı, birinci vektörü elde etmek için, ikinci vektörle toplanması gereken bir vektördür. Bu durumda A – В vektörü, Şekil 7b’ de gösterildiği gibi, ikinci vektörün ucundan, birinci vektörün ucuna doğru çizilen vektördür.
Vektörlerin Özellikleri İle İlgili Örnek
Bir otomobil, Şekil 8’deki gibi kuzeye doğru 20,0 km ve sonra 60.0° kuzey-batı yönünde 35,0 km yol almaktadır. Otomobilin bileşke yer değiştirmesinin büyüklük ve yönünü bulunuz.
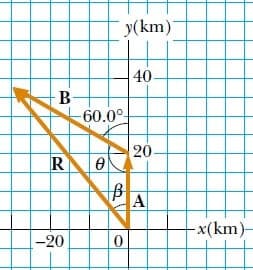
Çözüm:Bu örnekte, iki vektörün bileşkesini bulmak için iki yol gösteriyoruz. Problem, Şekil 8′ de görüldüğü gibi, grafik kağıdı ve bir iletki kullanılarak geometrik olarak çözülebilir. (Gerçekte, hesaplamayı başarabileceğinizi bilseniz bile sonucu kontrol etmek için vektörleri çizmelisiniz.) Bileşke R yerdeğiştirmesi, ayrı ayrı iki A ve B yer değiştirmesinin toplamıdır.
Problemi cebirsel olarak çözmek için. R’nin büyüklüğünü bulmak da trigonometrideki kosinüs teoremi kullanılabilir . θ= 180° – 60° = 120° ve R2 = A2 + B2 – 2AB cosθ olduğundan;
R’ nin kuzey yönünden itibaren ölçülen yönü, trigonometrideki sinüs teoreminden aşağıdaki şekilde elde edilebilir;
Böylece, otomobilin bileşke yerdeğiştirmesi, 38,9° kuzey batı yönünde 48,2 km’dir. Bu sonuç grafik olarak bulduğumuzla uyuşur.
Bu yazımızda sizlere vektörlerin özellikleri ve vektörlerin özellikleri ile ilgili örnek çözdük. Diğer yazımızda görüşmek üzere.




