Mükemmel gaz hal denklemi basit olmakla birlikte kullanım alanı sınırlıdır. Maddelerin P-v-T ilişkilerini daha geniş sınırlar içinde herhangi bir kısıtlama olmadan ifade eden hal denklemlerine gerek duyulur. Bu denklemler doğal olarak daha karmaşıktır. Bu amaçla önerilen çok sayıda denklem vardır, fakat burada sadece üçü ele alınacaktır. Van der Waals denklemi, bu denklemler içinde en eskisi olduğu için incelenecektir. Beattie-Bridgeman denklemi hassas sonuçlar veren ve bilinen bir denklem olduğu için ele alınacaktır. Benedict-Webb-Rubin denklemi ise hem en yenilerden biri hem de çok hassas olduğu için incelenecektir.
Van der Waals hal denklemi
1873 yılında önerilmiştir ve maddenin denklemleri öne sürülmüştür, kritik noktadaki davranışından belirlenen iki sabiti vardır. Van der Waals denklemi aşağıda verilmiştir.
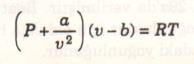
Benedict-Webb-Rubin Hal Denklemi
Benedict, Webb ve Rubin, Beattie-Bridgeman deklemini sabit sayısını sekize çıkararak geliştirdiler. Bu denklem aşağıda verilmiştir.
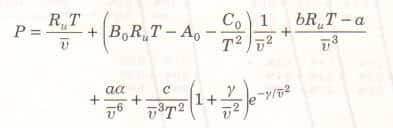
Etki Katsayılı Hal Denklemi
Bir maddenin hal denklemi seri toplamı olarak da ifade edilebilir.
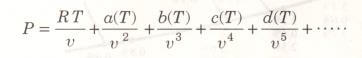
Bu ve buna benzer denklemler etki katsayılı (virial) hal denklemleri, sadece sıcaklığın fonksiyonu olan a(T), b(T), c(T), … ve benzeri katsayılar da etki katsayıları diye adlandırılır. Bu katsayılar deneysel olarak veya istatistik mekanikten teorik olarak elde edilebilir. Doğal olarak basınç sıfıra giderken etki katsayıları da sıfıra yaklaşacak, böylece denklem mükemmel gaz hal denklemi indirgenmiş olacaktır. Bir maddenin P-v-T ilişkisi, etki katsayılı hal denklemini kullanarak ve yeterli sayıda terim alarak, daha geniş bir aralıkta hassas olarak ifade edilebilir. Yukarıda açıklanan tüm denklemler maddenin gaz fazına uygulanmalıdır. Bu nedenle sıvı fazı veya sıvı-buhar karışımı için kullanılmamalıdır.
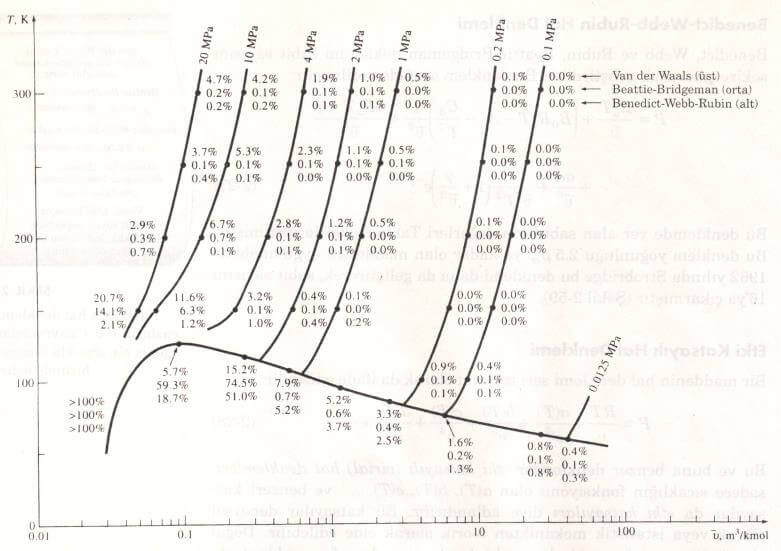
Bir maddenin P-v-T ilişkisini karmaşık hal denklemleriyle ifade etmek ve hesapları bir bilgisayar aracılığıyla yapmak mümkündür. El hesapları için daha basit hal denklemleri veya özelik tablolarının kullanımı tercih edilmelidir. Bu özellikle özgül hacmin hesaplanması gerektiğinde geçerlidir, çünkü deneme yanılma işlemi gerekecektir. Van der Waals, Beattie-Bridgeman ve Benedict-Webb-Rubin denklemlerinin hassaslıkları aşağıda karşılaştırılmıştır. Bu şekilden, Benedict-Webb-Rubin hal denkleminin diğerlerinden daha hassas olduğu açıkça görülmektedir.


