Bu yazımızda sizlere türeve farklı açıdan bakacağız. Öncelikle türev nedir ve türevin anlamını açıklacağım, daha sonra türev alma formüllerini göstereceğim. Pencereden sızan ışık önündeki kağıda vuruyordu ‘bir de bu çıktı’ diye söylenmeye başladı içinden. Uzattığı lisans eğitiminin belki de son sınavındaydı ama belki… Dakikalar geçiyor, süre daralıyordu, önündeki kağıda defter kenar süsü şeklinde bir şeyler karalamaya başladı. Güneşin de etkisiyle dikkati kaybolmuştu, dağılıyordu…
Okulunu uzatıp annesinin 1 sene daha aynı ayakkabıyla idare etmesini istemiyordu. Zaten bu yük altında ezilmişti bu sene… Okulunu uzattığının bilincinde olduğu her gün annesi eskiyen ayakkabısıyla kamburunda geziyordu sanki… Bu düşüncelerle aniden silkindi, devam etmesi gerektiğinin farkına vardı. Hoca gaddardı, yaz okulu kaldırılmıştı, geçen seneki tek ders sınavında kimsenin geçemediğini de öğrenmişti, kaçacak deliği yoktu bunun bilincindeydi…
Aslında zekiydi bu sınava da çalışmıştı hem de lisans hayatı boyunca hiçbir sınava çalışmadığı kadar. Fakat hoca yine numarasını yapmıştı, okulda saldığı namının hakkını da veriyordu hani! Önündeki kağıda baktı, toplamaya başladı; 20, 5, buraya da 10 verse toplamda 35… Cık dedi, önündeki kağıtla geçemezdi bunun farkındaydı. Aslında bir sorunun cevabını biliyordu ama o kadar heyecanlanmıştı ki tonla karışık formüllerin içinde ivmenin formülünü hatırlayamamıştı, bildiğimiz ivmenin… Bu yüzden atlamıştı o soruyu çünkü sorunun hemen başında ivmeyi bulup cevaba öyle devam etmesi gerekiyordu. Başka sorularda da kalem oynatamıyordu o derece zorlamıştı hoca. Sonuçta biliyordu ki, ivme yoksa geçmek de yok!
Dikkatini tekrar toplamıştı artık, ivmenin formülünü düşünüyordu. İvmenin tanımını da biliyordu ‘hızın değişimi’ diyordu kendi kendine. Hızın değişimi, hızın değişimi, hızın değişimi!.. Allah kahretsin değişimi de bu değişimi nasıl simgeleyeceğim, ne açıklar ki bu değişimi? Düşünüyordu… Hızın değişimi, hızın değişimi… 1 yıl daha kaybettireceksin bana 1 yıl!
Düşünürken, uyuduğu için hocası tarafından uyarıldığı bir matematik dersi geldi aklına. İlk sınıftaydı. Bu uyarılma belki korkudan, belki utançtan belki de başka bir sebepten, bir süre onun o derse odaklanmasını sağlamıştı. Bir cümle hatırlıyordu o derse ait, hocası ‘ Birbirine bağımlı değişkenlerde bir değişim varsa orada türev ve integral arayın!’ demişti. Birden bire zihninde bir fırtına koptu… Değişim dedi, evet değişim! İvme hızın değişimidir ve değişim varsa türev ve integral vardır. Şimdi yapması gereken iki şey vardı:
Hızın fonksiyonunu yazmak ve integral mi yoksa türev mi kullanacağını çözmek.
Birinci sorun onun için önemli değildi çünkü zaten hızın v=x/t denklemi ile ifade edildiğini sınavın başından beri çok berrak bir şekilde biliyordu. Sıra ikinci soruna geldi. Süre azalıyordu çabuk davranması gerektiğini iyi biliyordu. Düşüncenin gücünü az önce yeniden öğrendiği için tekrar düşünmeye koyuldu. Birden aklına, üniversite sınavlarına hazırlanırken yüzlerce kez çözdüğü integralde alan soruları geldi ayrıca lisans eğitimi boyunca çözdüğü sorular da… Bu sorularda genelde doğrusal olmayan fonksiyonların grafikleri altında kalan alanlar hesaplanıyordu. Zihninde şunun gibi bir şekil belirdi:
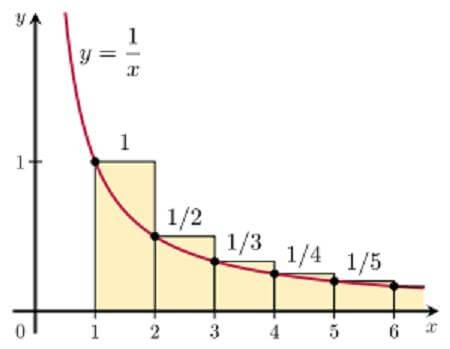
Bu şeklin ne anlama geldiğini biliyordu zira doğrusal olmayan şekillerin alanları üçgen, kare vs. gibi basit formüllerle ifade edilemezdi, bu nedenle integral alınıyordu. Bu integralin amacı şekilde görülen alanı sonsuz sayıda ve küçüklükte doğrusal şekillere bölerek bunların alanını hesaplayıp toplam alanı bulmaktı. Sonuçta sonsuz küçük bir cismin eğrisel olup olmaması, alanında bizim tahayyül edebileceğimiz bir fark oluşturmayacaktı. İntegralin değişimlerin toplamı olduğu kanaatine vardı ama ona değişim lazımdı toplamı değil…
Tüm bu fırtınalardan sonra ne yapacağını biliyordu. Hız fonksiyonunun zamana göre türevini alacaktı çünkü hızın zamanla değişiminin ivmelenme olduğu gün gibi ortadaydı. Hemen işe koyuldu v=x/t fonksiyonunun zamana göre türevini almaya koyuldu, bu işlem ufak bir bölümün türevi bilgisiyle yapılabilirdi.
∂v(t)/∂t=(∂x(t))/∂t=-x/t²
Yukarıdaki şekilde türev alma işlemini tamamladı ama daha tamamlamadan zihninde ivmenin formülü belirmişti. Formül a=xt² den ibaretti… İvme formülüyle beraber ivmeyi bulduktan sonra gerisi çorap söküğü gibi gelecekti, geldi de… Sınavdan 55 alarak dersi geçip mezun olmuştu. Kamburu gitmişti geleceğe karşı daha dik duruyordu zira çöp yığınlarının arasından elmasa ulaşmış ve onu değerli kılacak bir işleme ile işlemişti. O çöp uzun vadede ve pratikte hiçbir işe yaramayan ezberdi…
Evet arkadaşlar yazının etkisini bozmamak amacıyla yazının başında bir giriş yapmadım. Bu yazımda çeşitli nedenlerle çoğumuzun ne yaptığını bilmeden senelerce kullandığı türevin, formülünden değil anlamından bahsedeceğim.
Hatırlayın matematik hocalarımızın türev dersine girişi nasıl yaptığını, “Arkadaşlar bugün üniversite sınavında (atıyorum) 10! tane soru çıkan türeve geçiyoruz. İlk önce türevin genel formülü ile başlayalım, f^'(x)=(f(x+h)-f(x))/h”… 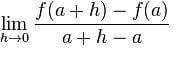
Türev dersi böyle başlar ve f(x)=x² fonksiyonunun türevinin nasıl alınacağı örneğiyle devam eder. İyi de,
Türevin anlamı nedir? Türevin kelime anlamı nedir? Türev nerelerde kullanılır? Türev nedir ne işe yarar? Türev diğer bilimlerin gelişmesi için nasıl bir anahtar olmuştur, örnekler nelerdir?
Yok, yok, yok hiçbirinin bir cevabı yok! Konunun başında anlatılmayan şeyler elbette devamında da anlatılmaz ve öğrenci sınavlarda ne yaptığını bilmeden bir şeyler çözmeye devam eder. Öğrencinin kendisinin merak edip araştırmaması da ayrı bir konu tabi…
Size konuya hala tam olarak girmemiş gibi gözüküyorum değil mi? Lakin durum öyle değil. Bence aslında konuyu neredeyse tamamlamış bulunuyorum. Çünkü bence en etkili anlatma tekniği konuyu insanların ilgi alanına dahil olan örneklerle en basit düzeye indirgeyerek anlatmaktır ve ben bunu yukarıda uygulamaya çalıştım. Bu nedenle yazıya bir hikayeyle başladım ve bu hikayeyi ve dolayısıyla türevin esas anlamını unutmayacağınızı düşünüyorum.
İşin cilasına gelelim, biraz daha tekniğe girelim. Türevin genel anlamını yukarıdaki hikayeden rahatlıkla anlayabilirsiniz. Bunu biraz daha örneklendirelim. Ne demişti hikaye kahramanının üniversitedeki matematik hocası: “Birbirine bağımlı değişkenlerde bir değişim varsa orada türev ve integral arayın“. Evet, bu değişim bir aracın frenleme sitemiyle oluşan diskteki ısı artışı ve sonrasındaki soğumanın disk üzerinde oluşturacağı kılcal çatlamaların sıcaklık değişim miktarına göre boyutunun değişimi olabilir, bu değişim yağmur hızına göre barajdaki su hacminin değişimi olabilir, bu değişim gazete bayiindeki gazetelerin gün içindeki saatlere göre satış hacmindeki değişim bile olabilir. Burada önemli olan birbirine bağlı değişkenlerin fonksiyonun kurabilmektir. Şimdi tekrar matematikten bir örnek verelim. Çoğumuz şu şekildeki,
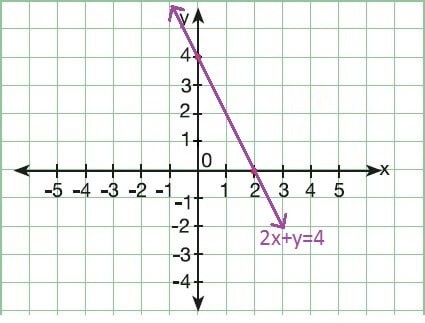
grafiğin doğrusal bir fonksiyonun grafiği olduğunu ve doğrusal fonksiyonların y=ax+b şeklinde ifade edildiğini biliyoruzdur. Bu fonksiyondaki değişkenler x, y; sabitler a, b (lütfen harflere takılmayınız x, y yerine α,β ya da aklınıza gelen herhangi bir simge de kullanabilirsiniz, kalıplara karşıyız) dir. Şimdi öylesine (?) fonksiyonun x değişkenine göre türevini alacak olursak türev: y’=a+0=a (sabitin yani b’nin türevi ‘0’dır) şeklinde bir şey elde ederiz. Doğrusal grafiklerin eğiminin sabit olduğunu yani değişmediğini biliyorsak (ya da en azından tahmin edebiliyorsak) ufkumuzun açıldığını hissetmeye hazır olalım.
Az önce bir cümle kullandık “değişmediğini biliyorsak” dedik. Durun bir dakika! Eğim değişmiyorsa ve değişim türevle açıklanıyorsa eğim ve türev arasında bir ilişki var demektir. Demek ki az önceki aldığımız türev “öylesine” değildi. Evet, bilmeyenler için söyleyelim bir fonksiyonun türevi o fonksiyonun eğimini verir. Ayrıca yukarıda aldığımız türev sabit bir sayıyı veriyor çünkü doğrusal fonksiyonların eğimi sabittir. İşte senelerce anlamını ve ne işe yaradığını bilmeden kullandığımız türev bu…
Türev Alma Kuralları

Bazı arkadaşlarımız verilen örneklerin çok basit olduğunu düşünebilirler. Evet bu doğru… Elbette ben de bilebilirdim (atıyorum) potansiyel enerjinin yükseklik değişimine göre türevini almayı oradan yükseklik eğrisinin oluşturulmasını (eğimden) oradan kinetik enerjiye geçmeyi, yazıyı formüllere-türevlere-integrallere boğmayı vs. ama konumuz üniversitedeki dinamik dersi veya mühendislik fiziği- matematiği değil. Kişisel görüşüm, bir şeyi yeterince basit bir düzeye indirip anlatmadığımız sürece ne etkili bir anlatım tekniğine ne de geniş zümrelere hitap eden bir sonuca ulaşamayız. Ayrıca bu yazıda bir amacım daha vardı o da, “En Küçük Kareler Yöntemi Nedir?” isimli ilk yazım ile doğrudan ilgili olan konulara girebilmek. Çünkü devamında naçizane olarak türev kullanılan bölümlere girmeye çalışacağım… Einstein’ın bir sözüyle yazımızı bitirelim…
“Eğer basit bir şekilde anlatamıyorsan, o konuyu iyi anlamamışsın demektir”


