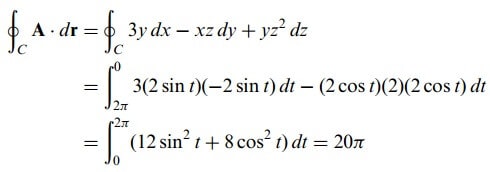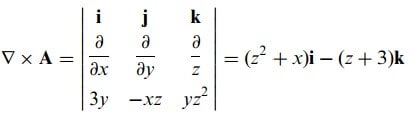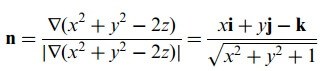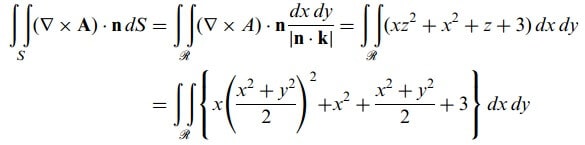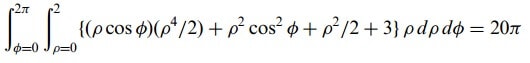Merhaba arkadaşlar bugünkü yazımızda sizlere stokes teoremi ve konuyu daha iyi kavramanız için stokes teoremi ile ilgili örnek çözeceğim. S, kendi kendini kesmeyen kapalı (basit kapalı eğri) bir C eğrisi ile sınırlanan, açık iki yanlı bir yüzey olsun. S nin bir tarafında bulunan yönlendirilmiş normali pozitif ve diğer yanındakini negatif alalım. Hangi tarafın pozitif seçileceği keyfidir, ancak buna önceden karar verilmelidir. Başı pozitif normal doğrultusunu gösteren bir gözlemci S nin sınırı üzerinde yürürken eğer yüzey solunda kalıyorsa C yi pozitif veya pozitif yönlü olarak adlandırırız. Bu takdirde, eğer A1, A2, A3 uzayın S yi kapsayan bir bölgesinde tek değerli, sürekli ve birinci mertebeden sürekli türevlere sahip ise,
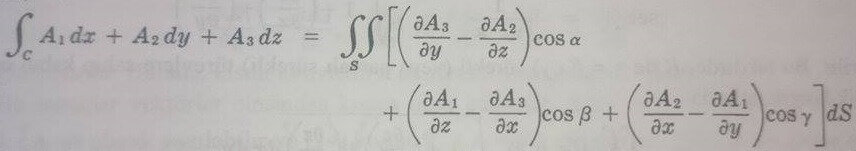
elde edilir. A = A1i + A2j + A3k ve n = cosαi + cosβj + cosγk olmak üzere, vektör gösteriminde bu, daha basit olarak
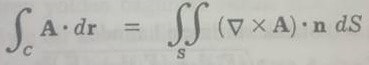
ile ifade edilir.
Stokes teoremi olarak adlandırılan bu teorem, A vektörünün teğetsel bileşeninin basit kapalı bir C eğrisi üzerinde alınan inin, A nın dönelinin normal bileşeninin C yi sınır olarak kabul eden herhangi bir S yüzeyi üzerinde alınan yüzey integraline eşit olduğunu ifade eder. Eğer özel olarak (eşitlik 2) de ∇ x A = 0 ise sonuç(eşitlik 3)
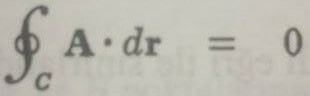
elde edeceğimize dikkat ediniz.
Stokes Teoremi İle İlgili Örnek
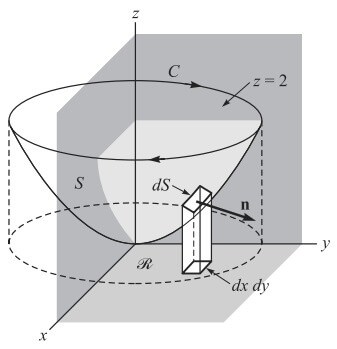
S, 2z = X2 + y2 paraboloidinin z = 2 ile sınırlanan yüzeyi ve C onun sınırı olmak üzere A = 3yi – xzj + yz2k için Stokes teoremini gerçekleştiriniz.
S nin C sınırı X2 + y2 = 4, z = 2 denklemleri ve z = 2cost, y = 2sint, z = 2, parametrik denklemleriyle verilir.
Bu taktirde
bulunur.
Ayrıca
ve
O zaman
olur.
Kutupsal koordinatlarda bu
haline gelir. Bu yazımızda sizlere stokes teoremini anlattım. Diğer yazımızda bu konu ile bağlantılı olan diverjans (uzayda green veya ıraksama) teoremini anlatacağım. Diğer yazımızda görüşmek üzere.