Denge terimiyle, cismin ya durduğu ya da kütle merkezinin sabit hızla hareket ettiği vurgulanmış olur. Biz, duran veya statik dengede olan cisimlerle ilgileneceğiz. Statik denge, mühendislik uygulamalarında genel bir durumu temsil eder ve onun kapsadığı prensipler, köprüler ve binalar gibi değişik yapı tasarımları yapan inşaat mühendisleri, mimarlar ve makine mühendisleri için özellikle önemlidir. Bu yüzden, mühendislik eğitimi gören öğrenciler ileride ayrıca yeterli statik dersi alacaklardır.
Bu bölümün son kesimi, etki altında bozulan cisimlerin gerçek durumlarıyla ilgilidir. Bozulma kavramı, maddelerin mekaniğini anlamada ve yapısal tasarımlarda önemli bir yer tutar. Bazı bozulmalar genellikle esnek karakterlidirler ve denge şartlarını etkilemezler. Esnek terimi ile, bozucu kuvvet ortadan kalktığında, cismin ilk şekline geri dönmesi özelliğini ifade ederiz. Her biri farklı bir bozulma tipine karşı gelen, birçok esneklik sabiti tanımlanmaktadır.
Denge Şartları
Bir cisme etki eden net kuvvetin sıfır olması, dengenin gerek şartıdır. Cisim tek bir parçacık olarak ele alınabilirse, parçacığın dengede olması için sağlanması gereken tek şart budur. Gerçek cisimlerle ilgilenildiğinde, onların her zaman parçacık olarak ele alınmaları mümkün olamadığından, durum daha karmaşık olmaktadır. Gerçek bir cismin statik dengede olabilmesi için, ikinci bir şart daha sağlanmalıdır. Bu ikinci şart gerçek cisim üzerine etki eden net torku içerir. Dengenin hareketsizliği gerektirmediğine dikkat edelim. Buna örnek olarak, dönen bir cisim sabit açısal hıza sahip olabilir ve hala dengededir.
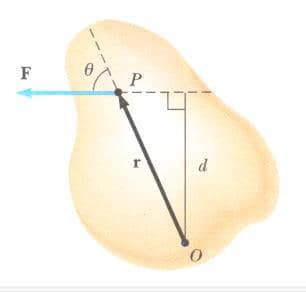
Şekil 1’de gösterildiği gibi, katı cisme etki eden tek bir F kuvvetini ele alalım. Kuvvetin cisim üzerindeki etkisi, kuvvetin uygulandığı P noktasının yerine bağlıdır, r, P ’nin 0 noktasına göre yer vektörü ise, F kuvvetinin 0 noktasına göre oluşturduğu dönme momenti (tork), aşağıdaki eşitlik ile verilir:
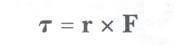
Vektörel çarpım tartışmasında т vektörünün, r ve F vektörleri tarafından belirlenen düzleme dik olduğunu hatırlayınız, т’nin yönünü tayin etmek için sağ el kuralını kullanabilirsiniz.
Şekil 1’den de görebileceğiniz gibi, F kuvveti, cismi 0 noktası etrafında F ’nin büyüklüğü yanında, d moment koluna da bağlı olarak döndürme eğilimindedir. (Burada d, 0 ’dan kuvvetin etki çizgisine olan dik uzaklıktır). т’un büyüklüğü, tanıma göre Fd ile verilir. Şimdi katı cisim üzerine önce F1 sonra F2 kuvvetinin etki ettiğini varsayalım. Bu iki kuvvet aynı büyüklüğe sahipse, sadece aynı doğrultu ve aynı yönde iseler ancak o zaman cisim üzerinde aynı etkiye sahip olabilirler. Bir başka deyişle, F1 ve F2 gibi iki kuvvet ancak ve ancak F1 = F2 ise ve ancak ve ancak verilen herhangi bir noktaya göre aynı torka sahipseler, eşdeğerdir.
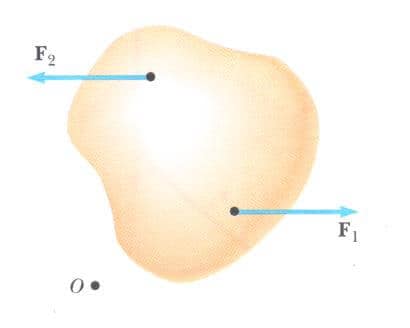
Eşdeğer olmayan kuvvetlere, Şekil 2’deki gibi, büyüklükleri eşit, doğrultuları paralel ve yönleri zıt iki kuvvet örnek olarak gösterilebilir. Sağa doğru yönelen kuvvet, cismi O’dan geçen ve şekil düzlemine dik bir eksen etrafında saat yönünde döndürmeye çalışırken, sola doğru yönelen kuvvet, aynı cismi O noktası etrafında saatin tersi yönünde döndürmeye çalışır.
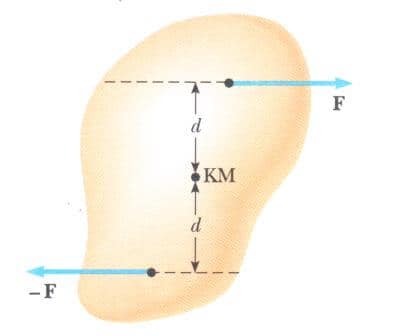
Cismin Şekil 3’de gösterildiği gibi kütle merkezinden geçen bir eksen etrafında dönebilecek şekilde tutturulduğunu farz edelim. Etki çizgileri cismin kütle merkezinden geçmeyen, büyüklükleri eşit ve yönleri zıt iki kuvvet, şekilde gösterildiği gibi, bu cisme etki etmektedir. Bu şekilde etki eden kuvvetlerin oluşturduğu İkiliye kuvvet çifti denir. (Şekil 2’deki iki kuvvet de kuvvet çifti oluşturur). Bir kuvvet çiftindeki kuvvetlerin Newton’un üçüncü yasasının bir sonucu olduğunu düşünme hatasına düşülmemelidir. Onlar üçüncü yasa kuvveti olamazlar çünkü onlar aynı cisim üzerine etki etmektedirler. Üçüncü yasaya göre kuvvetler farklı cisimler üzerine etki etmektedir. Kuvvetlerin her biri aynı Fd büyüklüğünde torka sahip olduklarından, net torkun büyüklüğü 2Fd ile verilir. Açıkça, cisim saat yönünde dönecek ve bu eksen etrafında bir açısal ivmeye sahip olacaktır. Bu, dönme hareketini incelediğimiz şu ana kadar, dengenin sağlanamadığı bir durumdur. Yani, cisim üzerine etki eden “dengelenmemiş” (veya net) dönme momenti, ∑т = 2Fd = lα bağıntısına uygun olarak bir α açısal ivmesinin doğmasına sebep olur.
Genel olarak, bir cisim sadece onun açısal ivmesi α=0 ’sa, dönme dengesine sahip olacaktır. Sabit bir eksen etrafındaki dönme için, Σт = lα olduğundan, herhangi bir başlangıç noktasına göre net torkun sıfır olması, bu cismin dengede olabilmesinin ikinci gerek şartıdır. Böylece, bir cismin dengede olabilmesi için, iki şartın sağlanması gerektiği görülmektedir. Bu şartlar:
- Dış kuvvetlerin bileşkesi sıfır olmalıdır. ∑F = 0
- Herhangi bir dönme eksenine göre dış torklarm bileşkesi sıfır olmalıdır. ∑т = 0
İlk şart, öteleme dengesini ifade eder. Yani, verilen bir eylemsizlik referans sisteminden bakıldığında, cismin kütle merkezinin çizgisel ivmesinin sıfır olması gerekir. İkinci şart, dönme dengesini ifade eder. Yani, herhangi bir eksene göre açısal ivme sıfır olmalıdır. Bu bölümün ana konusu olan statik denge özel halinde, cisim durgun haldedir, bu yüzden de çizgisel veya açısal hıza sahip değildir.
Statik Dengedeki Katı Cisimlere Örnekler





