Bu yazım sonsuzluk ne demek ve sonsuzluk üzerine paradokslar hakkında olacak. Önceleri, koyun otlatmaya çıkan bir çoban, akşam eve geldiğinde, evden çıktığındaki koyunlarla eve girdiğindeki koyunlarının sayısının eşit olduğunu görmek için şu sistemi kullanırdı: Koyunlarını ahırdan teker teker çıkarır ve her çıkardığı koyun için kenara bir taş ayırırdı. En son koyun çıkana kadar sabırla bekler ve son koyunla birlikte taşları başlarına bir zarar gelmeyecek şekilde ahırın kapısında muhafaza ederdi. Akşam eve geldiğinde ise koyunlarını teker teker ahıra sokar ve her ahıra giren koyun için sabah ki ayırdığı taşlardan birer birer eksiltirdi. Eğer, sabah ki ayırdığı taşlar tamamı ile biterse koyunlarını eksiksiz eve getirmiş olurdu. Ama eğer elinde taş artarsa elindeki her bir taş bir tane koyunu simgelediğinden elindeki taş kadar koyunsuz eve dönmüş olacaktı.
İnsanoğlu var olduğu günden beri, gördüğü nesneleri, duyduğu sesleri, hissettiği şeyleri (fiziksel ve psikolojik) sorgulama eğilimindedir. Zamanla somutik (somut olan) kavramların yanı sıra soyut idealarda insanoğlunun düşüncelerine hüküm sürmeye başlamıştır. “Var olan” şeyleri düşünen insanoğlu, “var olabilecekleri” de düşünmeye başlamıştır. Var olandan ziyade “var olmuş” “var olabilecek” şeyler daha çok ilgi çekmeye başlamıştır.
Önceleri, “1” “2” “3” … gibi sembollerin varlığından yoksunduk. Ve ister istemez zorluklar çekmekteydik. (yukarıdaki anlatılan örneği ele alabiliriz) Ancak şu sıralar, hesaplamaları saniyeler içerisinde yapabiliyor ve de gayet tutarlı cevaplar alabiliyoruz. Bu tutarlılık içerisinde Anaksimandros [610-546] ile başlayan “sonsuzluk” furyası milat öncesinden günümüze akılları bir hayli zorlamıştır. Günümüzde dahi kavramsal anlaşılmazlıkların doğurduğu ifade eksiklikleri, ettiğimiz kabullerin tutarsızlıklarını bir hayli net bir şekilde göstermektedir. “Sonsuzluk” terimindeki kavramsal karışıklığı en aza indirmek için bu yazıyı ele alıyorum.
Sonsuzluk Üzerine Paradokslar
Akhilleus ve kaplumbağa paradoksu:
Yunan kahramanı Akhilleus’un, bir kaplumbağa ile yarış yaptığını hayal edelim. Çok iyi bir koşucu olduğu için Akhilleus, kaplumbağanın belirli bir mesafe, örneğin yüz metre, ileriden başlamasına izin verir. Eğer her ikisinin de sabit hızlarda koştuğunu düşünürsek (biri sabit yüksek bir hızda, diğer sabit düşük bir hızda), belirli bir süre sonra Akhilleus yüz metre koştuğunda, kaplumbağanın başladığı yere gelmiş olacaktır; bu süre boyunca kaplumbağa da küçük de olsa belirli bir mesafe koşmuştur, örneğin 1 metre. Akhilleus bir süre sonra bu mesafeyi de tamamladığında, o süre zarfında kaplumbağa yine küçük de olsa bir mesafe ilerlemiş olacaktır ve bu böyle devam edecektir. Böylece, Akhilleus ne zaman kaplumbağanın varmış olduğu bir noktaya varsa, daha hâlâ gitmesi gereken bir mesafe kalmış olacaktır.

Bu nedenle Zenon, Akhilleus’un kaplumbağayı hiçbir zaman geçemeyeceğini söylemiştir. Amacı mantıksal düşünme bakımından hareketin imkansızlığını göstermektir.
Dikotomi Paradoksu:
A kişisinin d noktasına gitmesi gerektiğini hayal edelim. Fakat d’ye gitmeden, önce d’ye olan mesafenin yarısını gitmek zorundadır. Fakat d’ye olan mesafenin yarısını gitmeden önce bu mesafenin çeyreğini gitmesi gerektir. Daha sonra çeyreği gidebilmek için sekizde birini gitmesi gerekmektedir; bu böyle devam eder.
A-{d}\{8}-{d}\{4}—{d}\{2}——-d
Sonuç olarak A kişisinin sonsuz sayıda mesafe gitmesi gerekir. Bu seride bir sorun daha vardır; her ilk mesafe aralığı ikiye bölünebileceği için gidilmesi gereken belirli bir ilk mesafe yoktur. Böylece bu yolculuğun bir başlangıç noktası yoktur, yani yolculuğa başlayamaz. Bu paradoks sonuç olarak belirli bir mesafenin yolculuğunun tamamlanamayacağını veya başlanamayacağını, böylece de her hareketin sadece bir illüzyondan ibaret olacağını ifade etmektedir.
Ok Paradoksu
Yaydan çıkmış ve ilerleyen bir ok, zaman içindeki her anda belirli bir konumdadır. Eğer an belirli, tek bir nokta ise o anda okun hareket etmeye zamanı yoktur ve durağandır. Bu nedenle gelecek anların hepsinde de durağan yani hareket etmeyen şekilde olması gerektir. Böylece ok her zaman durağandır ve hareket etmez; hareket imkansızdır.
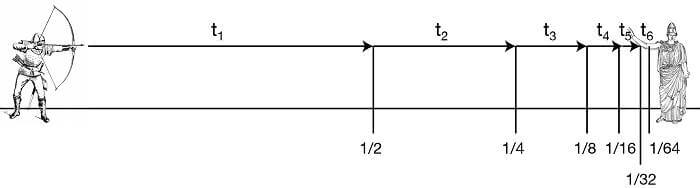
Yukarıda okuduğunuz 3 paradoksta antik yunan filozofu Elealı Zenon’ a aittir. Zenon’ nun ortaya attığı bu paradokslar ilk okumada ilginç gelse de, “sonsuzluk” kelimesinin, ifade ettiği anlamı net olarak karşılayamamasından kaynaklanmaktadır.
Sonsuzluğun İrdelenmesi
Matematik, kanaatimce bir keşiftir, hatta icat süsü verilmiş bir dengeler sistemi de diyebiliriz. Birçok bilim dalının temelini oluşturmuş matematik bilimi, fizik bilimi ile de bir hayli içli dışlıdır. Ancak matematiksel bazı ifadeler fiziksel bazı ifadelerle ters düşebilir. Bunlardan biriside sonsuzluk kavramıdır. Yukarıda verilen paradokslardan olan “Arkhilleus ve Kaplumbağa” paradoksunu ele alırsak; matematiksel olarak Arkhilleus’un kaplumbağa’yı geçmesi gerçekten olanaksızdır. Çünkü Zenon’un da belirttiği gibi Arkhilleus kaplumbağanın yanına gelebilecek mesafeyi her katettiğinde kaplumbağa mesafeyi çok az da olsa her seferinde aşmış olacaktır. Bu mesafeler (sayı olarak düşünüldüğü için) böyle sürekli parçalana parçalana sonsuza kadar gidecek ve kaplumbağa hiçbir zaman geçilemeyecektir. Ancak fiziki hayatta böyle bir şey mümkün müdür? Tabii ki değildir. Kaplumbağa her halükarda geçilecektir.
Aslında Zenon’un bir yere kadar olan yaklaşımı doğrudur. Evet Arkhilleus kaplumbağanın her yanına gelişinde kaplumbağa bir miktar daha uzaklaşacaktır. Bu bir yere kadar geçerlidir. Fiziki anlamda bir yere kadar geçerlidir. Yani en son birim parçalanması “Planck uzunluğu” kadar olacaktır. Planck uzunluğu fiziksel anlamda bilinen, parçalanamaz en küçük uzunluktur. Sayısal olarak ifade edecek olursak; bir proton çapının 10−20 katına eşittir ve bu sayı bir atom çekirdeğinin çapının yaklaşık 10−13 cm olduğu düşünülürse bir hayli küçük bir sayı olduğu görülür. Planck uzunluğu altındaki bir mesafe biriminin olamadığını, en azından içerisinde bulunduğumuz uzay-zamanda bulunmadığını rahatlıkla söyleyebiliriz. Aynı şekilde zamansal kavramda ki ok paradoksunu da fiziksel anlamda çürütebiliriz. Yine parçalanamaz zaman birimi olan “Planck zamanı” (saniyenin 10−43 ten küçüktür) bu ok paradoksunu da yaşanılan fiziki boyutta açıklamaktadır.
Fiziksel olarak mantıklı bir cevap vermiş bulunmaktayız. Peki neden matematiksel olarak mantıklı bir cevap veremiyoruz? Neden matematik bu denli reel hayata ters düşüyor? Bir çok şeyin kabulden ibaret olduğu bu evrende neden matematiği kısıtlıyoruz? Aslında yukarıda ki bahsettiğim “Planck uzunlukları” gibi matematikte de parçalanamayan uzunluklar vardır. Bu sayı, Epsilon sayısıdır. Sıfıra en yakın sayı olarak bilinir ve (ε) ile sembollenir. Parçalanamayandan kastım sıfır ile arasında bir sayının olmamasıdır. Yani daha doğrusu olamaması gerekmektedir. Ama sembolist genel görüş maalesef bunun aksini iddia etmektedir. Ve hala epsilonla sıfır arasına bir sayılar topluluğu yerleştirmektedir.
Şimdi, benim vereceğim bir örnekle yazımıza devam edelim. Sıfır (0) ile Bir (1) arasında kaç tane sayı vardır? Cevabı aşikâr gibi duruyor, sonsuz. Cevabın, sayılamayacak düzeyde epsilondan (ancak sınırlı sayıda) oluştuğunu söylesek daha bir mantığa yatkın olduğunu görürüz sanki. Bu soruyu böyle havada sorarsak iki cümle arasında bir farkın olmadığını düşünürüz bir de şöyle soralım:
Şimdi elimize bir cetvel alalım. Ve kendimize göre bir başlangıç belirleyerek oraya 0 (sıfır) diyelim. Bitişe de 1 diyelim. Şimdi bir daha düşünelim: 0 ile 1 arasındaki sayı adedi sizce nedir?
Şimdi sonsuz diyemiyoruz değil mi? Aslında da 0 ile 1 arasında sonsuzluk mevcut değildir. Sonsuzluk ibaresinin matematikte ki yerini mi yanlış anlıyoruz diye soralım bu kez kendimize. Diyelim ki yukarıda anlatılan sonsuzlukla matematiğin bir ilgisi yok, matematikteki sonsuzluk kavramı bir “sıfat” olsun. Peki bir sıfatın sembole sahip ( ∞ ) olması ne kadar doğru? Bu sıfatın bir sembole sahip olması +∞ ibaresinin sürekli (sınırsız) artan bir şeyi ifade etmesi yahut -∞ ibaresinin sürekli (sınırsız) azalan bir şeyi ifade etmesi ne kadar doğru?
Bir şey ne kadar gerçeğe yaklaşırsa o derece güvenilirdir. Matematiğin mantık dışı cevaplar vermesi enteresan. Aslında mantık ve matematik çok yakın birer akrabadır. Ve bakın Bertrand Russel bu ilişkiyi nasıl açıklıyor:
“Matematik ve mantık, tarihin penceresinden baktığımızda, birbirinden tamamen ayrı disiplinler olmuştur. Matematik bilimle, mantık ise yunanca ile bağdaştırılmıştır. Ama son zamanlarda her ikisi de gelişmiştir; mantık daha matematikselleşmiş ve matematik ise daha mantıksal bir hal almıştır. Sonuçta, ikisi arasına bir çizgi çekmek artık [1919] tamamen imkansız hale gelmiştir; hatta ikisi bir olmuştur. Birbirlerinden ancak bir erkeğin gençliği ve yetişkinliği kadar farklıdırlar. Mantık matematiğin gençliği, matematik ise mantığın gelişmiş halidir.”
Özetle Russel matematiğin temelinde mantığın olduğunu savunmaktadır. Ve kanaatimce gayette haklıdır.
SON
Benim bu yazıdaki amacım limiti sorgulamak değildi, sürekli artanlar ve sürekli azalanlarda değildi bu yazının konusu. Yakınsamalara ıraksamalara girmedim bile yazıda. Ben sadece ufak bir soru sordum. “0 ile 1 arasında kaç tane sayı vardır?” bunun cevabına matematik eğer sonsuz demeye devam ederse reel hayattan hızla uzaklaşmaya devam edecektir. Düşünceler ve matematik soyut kavramlardır ama gerçekler üzerine düşünür ve yorum katarız. Eğer uygulamalar reel dışı olursa düşünceler ve matematik artık ne kendini ifade edebilir, ne de evreni!


