Siyah Cisim ışıması ve Planck Hipotezi

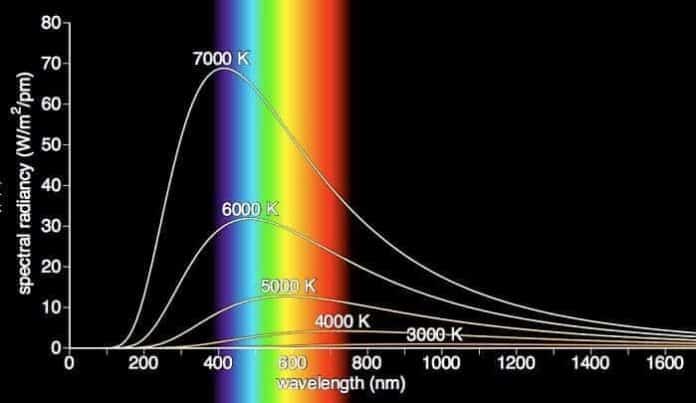
Merhaba arkadaşlar bu yazımızda siyah cisim ışıması ve planck hipotezi, rayleigh-jeans yasası, enerji düzeyleri ve siyah cisim ışıması ve planck hipotezine dair formüllerin türetilmesini sizlere anlatacağım. Herhangi bir sıcaklığa sahip bir cisim, bazen ısıl (termal) ışıma yapar. Bu ışımanın karak­eristikleri cismin sıcaklığı ve özelliklerine bağlıdır. Düşük sıcaklıklarda ısıl ışıma­nın dalga boyları, çoğunlukla elektromanyetik spektrumun kızılötesi bölgesin­dedir ve bu nedenle ışıma gözle görülemez. Cismin sıcaklık derecesi yüksel­dikçe cisim kızarmaya başlar bir başka deyişle yeteri kadar görülebilir ışıma ya­yınlandığı için cisim kırmızı renkte parlaklık kazanır. Yeteri kadar yüksek sı­caklıkta, cisim, ışık ampulünün sıcak tungsten filamanı gibi, beyaz renkte par­lar. Dikkatli bir inceleme ile cismin sıcaklığı yükseldikçe yayınladığı ısıl ışınının, spektrumun kızılötesi, görülebilir ve morötesi bölgesine yayılmış sürekli bir dalga boyları dağılımına sahip olduğunu gösterir.

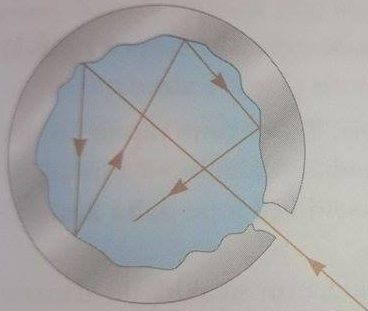
Klasik bakış ile ısıl ışıma, cismin yüzeyine yakın atomlardaki yüklü parça­cıkların ivmeli hareketlerinden kaynaklanır. Bu yüklü parçacıklar küçük an­tenlerin yapacağı gibi ışıma yayınlarlar. Isıl olarak oynaklaşan parçacıklar, cisim tarafından yayınlanan ışımanın sürekli spekturumuna neden olan bir ivme dağılımına sahiptirler. Ancak 19. yüzyılın sonlarında ısıl ışımanın klasik te­orisinin yetersiz olduğu ortaya çıktı. Ana problem bir siyah cisim tarafından yayınlanan ışımada dalga boylarının gözlenen dağılımını anlayabilmekti. Siyah cisim üzerine düşen bütün ışımaları yutan bir ideal sistemdir. Şekil 1 de görülen içi boş bir cisim üzerindeki delik, siyah cisim için iyi bir örnektir. Cisim içindeki oyuğa açılan delikten yayınlanan ışımanın doğası yalnızca oyuk duvarlarının sıcaklık derecesine bağlıdır ve du­varları oluşturan maddenin cinsinden bağımsızdır. Yanan linyit kömürü par­çaları arasındaki boşluklar siyah cisim ışımasına çok benzer bir ışık yayınlarlar.

Siyah Cisim ışıması ve Planck Hipotezi Formüllerinin Türetilmesi

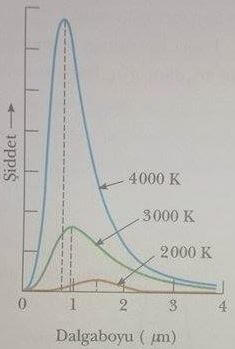
Şekil 2, siyah cisim ışıma enerjisinin sıcaklık ve dalga boyu ile nasıl değiştiğini göstermektedir. Siyah cismin sıcaklığı arttıkça iki belirgin özellik gözlenmektedir. Birinci etki dağılımın tepesinin daha kısa dalga boylarına doğru kaymasıdır. Bu kesimin başında ele alınan cismin ışık vermeme durumundan, (tepe kızıl ötesi bölgesinde) kızararak ışık vermeye başlaması (tepe yakın kızıl ötesi bölgesinde, dağılımın bir ucu görünür bölgenin kırmızı ucuna girmiş) ve beyaz ışık vermesi (tepe görünür bölgede) haline değişmesinin nedenidir. Bu kaymanın Wien Yerdeğiştirme Yasası adı verilen aşağıdaki bağıntıya uyduğu bulunmuştur.

λ_maxT = 2,898×10^-3m.K    (40.1)

buradaki λ_max eğrinin tepe yaptığı dalga boyu değeri, T ise ışıma yapan cismin mutlak sıcaklık derecesidir. Eğrinin tepe noktasındaki dalga boyu mutlak sı­caklık derecesi ile ters orantılıdır; yani sıcaklık yükseldikçe tepe daha kısa dalga boylarına doğru “kayar”.

İkinci etki, cismin yayınladığı toplam enerji miktarının sıcaklık ile artması­dır. Bu özellik P=σAeT⁴ şeklinde yazdığımız bu eşitlik Stefan Ya­sası ile belirlenir. I=P/A cisim için e=1 olduğunu hatırlayarak Stefan Yasası­nı I=σT⁴ şeklinde yazabiliriz.

Siyah cisimden yayınlanan enerji dağılımını incelemek için I(λ,T)dλ yı, dλ dalga boyu aralığında birim yüzeyden yayılan güç olarak tanımlamak kullanışlı olur. Rayleigh-Jeans Yasası olarak bilinen siyah cisim ışımasının klasik bir modeline dayalı hesabın sonucu

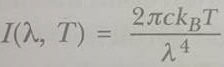
olarak bulunur, burada k_B Boltzmann sabitidir. Siyah cisim ışımasının bu kla­sik modelinde oyuk duvarlarındaki atomlar bütün dalga boylannda elektro­manyetik dalgalar yayınlayan titreşkenler (osilatör) takımı olarak ele alınırlar. Bu model, T ile orantılı olan, titreşken başına ortalama bir eneıji verir.

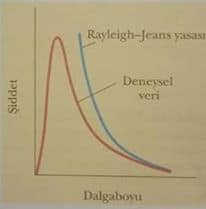
Siyah cisim ışıma spektrumununun deneysel bir grafiği Şekil 40.4 de Ray- leigh-Jeans yasasının teorik öngürüsü ile birlikte gösterilmiştir. Uzun dalga ­boylarında Rayleigh-Jeans yasası deneysel verilerle oldukça uyumludur, ancak kısa dalga boylarında belirgin bir uyumsuzluk vardır. Bu uyumsuzluğu λ sıfıra yaklaşırken Eş. 40.2 de verilen I(λ,T)fonksiyonunun sonsuza gittiğine dikkat ederek anlayabiliriz. Sonuç olarak siyah cisim spektrumunda kısa dalga boylarının baskın olmasının yanı sıra, siyah cismin ışıdığı enerji de sıfır dalga boyu limitinde sonsuz olmalıdır. Bu öngörü ile çelişkili olarak Şekil 40.4 de çizilen deneysel veriler λ sıfıra yaklaştığında I(λ,T) nin de sıfıra yaklaştığını gösterir. Teori ile deney arasındaki bu tutarsızlık öyle şaşırtıcı bir haldi ki, bilim adamları ona morötesi felaket adını verdiler. (Bu bir yanlış isimlendirmedir, çünkü “felaket”—sonsuz enerji—morötesi dalga boylarında değil, dalga boyu sıfıra giderken ortaya çıkar.)

Teori ile deney arasındaki bir diğer çelişki siyah cisim tarafından yayınlanan toplam güç konusundadır. Deneysel olarak 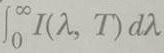 ile verilen birim yüzey başına toplam güç sonlu kalırken, Rayleigh-Jeans yasası (Eş. 40.2) bu değerin sonsuz olacağını öngürür.

1900 yılında Planck, siyah cisim ışıması için bütün dalga boylarında deneyle uyumlu olan bir bağıntı türetti. Planck’ın analizi Şekil 40.4 deki kırmızı eğ­riyi verir. Önerdiği fonksiyon

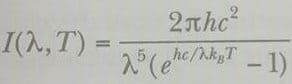
dır. Bu fonksiyon bir h parametresini içerir. Planck bu parametreyi, fonksiyo­nun tüm dalga boylarında deneysel verilerle uyumunu sağlayacak şekilde ayar­ladı. Bu parametrenin değerinin siyah cismin yapıldığı maddeden ve sıcaklık derecesinden bağımsız olduğu bulunmuştur, h değişken bir parametreden öte, bir temel doğa sabitidir. Önce Bölüm 11 ve sonra Bölüm 35 de gördüğü­müz Planck sabiti h nin değeri,

h= 6,626×10-34 J.s    (40.4)

dir. Uzun dalga boylarında Eş. 40.3 Rayleigh-Jeans ifadesine indirgenir ve kısa dalga boylarında deneysel sonuçlarla uyumlu olarak azalan dalga boyları için I(λ,T) nin üstel olarak azalacağını öngörür.

Planck, teorisinde siyah cismin yüzeyindeki titreşen moleküllerin doğası ile ilgili iki cesur ve tartışmaya açık varsayım yaptı:

1. Moleküller yalnızca

E_n = nhf          (40.5)

olarak verilen kesikli enerji değerlerine sahip olabilirler, burada n kuantum sayısı adı verilen pozitif bir tamsayı,f moleküllerin doğal titreşim frekans­larıdır. Bu, özdeş titreşkenlerin (salınıcı/osilatör) enerjisinin hareketin genliğine bağlı ve frekansından bağımsız olduğu klasik harmonik titreşken modelinden bütünüyle farklıdır. Bir molekülün enerjisi yanlızca Eş. (40.5 ) ile verilen kesikli değerleri alabileceği için, enerji kuantumlanmıştır denir. Her bir kesikli enerji değeri molekül için farklı bir kuantum durumuna ait­tir ve her bir n değeri belirli bir kuantum durumunu temsil eder. Molekül n = 1 kuantum durumunda iken enerjisi hf, n = 2 kuantum durumunda iken enerjisi 2hf vs. olur.

2. Moleküller, sonradan foton adını alacak kesikli paketler halinde enerji ya­yınlar ve yutarlar. Moleküller bir kuantum durumundan diğerine “sıçrayarak” bu fotonları yayınlar veya yutarlar. Sıçrama bir durumdan ona komşu daha aşağı duruma ise, Eş. 40.5, molekül tarafından tek bir foton olarak ya­yınlanacak enerji miktarının hf ye eşit olacağını gösterir. Buna göre iki komşu kuantum durumu arasındaki enerji farkına karşılık gelen bir foto­nun enerjisi

E = hf   (40.6)

olur.

Bir molekül yalnızca kuantum durumu değiştiğinde enerji yayınlar veya yu­tar. Şekil 40.5, kuantumlanmış enerji seviyelerini ve komşu seviyeler (durum­lar) arasındaki geçişleri göstermektedir.

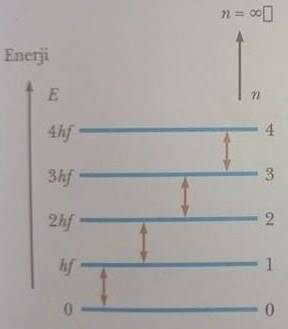
Planck kuramındaki kilit nokta, kuantumlu enerji durumları radikal var­sayımıdır. Bu gelişme kuantum teorisinin doğuşunu oluşturmuştur. Planck te­orisini ortaya attığında, bilim adamlarının çoğu (Planck’ın kendisi de dahil!) kuantum kavramının gerçekçi olduğunu düşünmemişlerdi. Bu nedenle Planck ve diğerleri, siyah cisim ışımasının daha akla uygun bir açıklamasını bulma çalışmalarını sürdürdüler. Ancak, sonradan ortaya çıkan gelişmeler, atomik seviyedeki pek çok diğer yörüngeyi (phenomena) açıklamak için ku­antum kavramına (klasik kavramlar yerine) dayalı bir teorinin kullanılması ge­rektiğini göstermiştir.

Siyah cismin ışıması ve planck hipotezi, rayleigh-jeans yasası, enerji düzeyleri ve siyah cismin ışıması ve planck hipotezine dair formüllerin türetilmesini sizlere mümkün olduğunca basitçe anlatmaya çalıştım. Diğer yazımızda görüşmek üzere.