Sıvıların Basıncı Konu Anlatımı

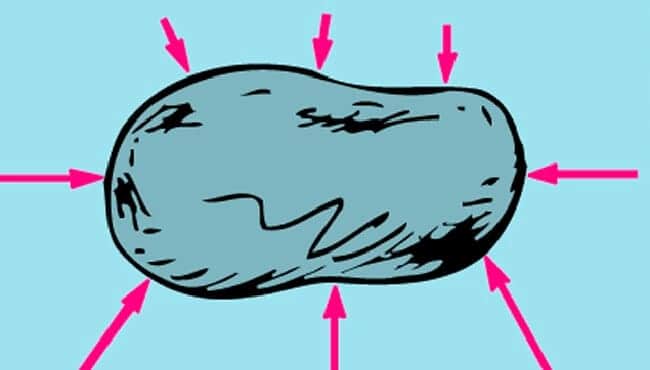
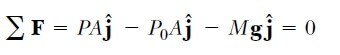Merhaba arkadaşlar bu yazımızda sizlere sıvıların basıncı konu anlatımı yapacağız. Sıvılar, makaslanma zorlarını ya da gerilme zorlarını durdurmaz; yani, bir sıvı içine daldırılan bir cisim üzerinde mevcut olan zor, cismi sıkıştırmaya çalışır. Başka bir ifadeyle cisim üzerine akışkan tarafından uygulanan kuvvet, Şe­kil 1’de görüldüğü gibi cismin yüzeylerine daima diktir.

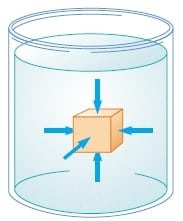
Sıvıların basıncı, Şekil 2’de gösterilen düzenekle ölçülebilir. Düze­nek, bir yaya bağlı hafif bir piston içeren havası boşaltılmış bir silindirden iba­rettir. Düzenek akışkan içine daldırıldığında akışkan, piston Ürerine aşağı doğru basınç uygular ve akışkanın içe doğru olan kuvvetiyle, yayın dışa doğru olan kuvveti dengeleninceye kadar yay sıkışır. Akışkanın basıncı, ölçeklendiril­miş bu yayla doğrudan ölçülebilir. Eğer piston üzerine uygulanan normal kuvvet F ve pistonun yüzölçümü A ise düzeneğin daldırıldığı seviyedeki akışkanın P basıncı, söz konusu kuvvetin yüz ölçüme bölümü olarak tanımlanır; yani,

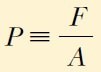
dır. Basıncın, pistona uygulanan kuvvetin büyüklüğü ile orantılı olan skaler bir nicelik olduğuna dikkat ediniz.

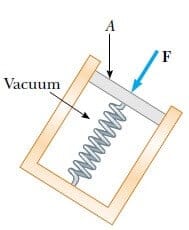
Belli bir noktadaki basıncı tanımlamak için, Şekil 15.2’deki düzeneğe etki eden bir akışkanı inceleyelim. Söz konusu noktadaki dA çok küçük yüzey ele­manına akışkan tarafından uygulanan kuvvet dF ise, o noktadaki basınç

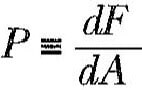
olur. Gelecek kesimde göreceğimiz gibi, akışkan içindeki basınç derinlikle de­ğişir. Bu nedenle, bir kabın düz yüzeyleri üzerindeki toplam kuvveti bulmak için yüzey üzerinden 1 eşitliğinin integralini almamız gerekir.

Basınç, birim yüzölçüm başına düşen kuvvet olduğu için, SI birim sisteminde N/m² biriminde olur. Basıncın SI birimindeki öteki adı Paskal (Pascal/Pa) dır. Yani;

1 Pa ≡ 1 N/m²       (Eşitlik 2)

dir.

Şekil 3′ te kar ayakkabıları, yumuşak karın içine batmanızı önler; çünkü onlar, kar üzerinde sizin oluşturduğunuz aşağı yünlü kuvveti büyük bir yüzölçüm üzerine yayar ve kar yüzeyindeki basıncı azaltır.

Sıvıların Basıncı Derinlik Nasıl Değişir

Sıvıların Basıncı Derinlikle Nasıl Değişir?; Dalgıçlar tarafından çok iyi bilindiği gibi, su basıncı derinlikle artar. Aynı şe­kilde, atmosfer basıncı yükseldik artışıyla azalır; bu nedenle, çok yüksekten uçan uçakların basınçlı kabinleri olmalıdır.

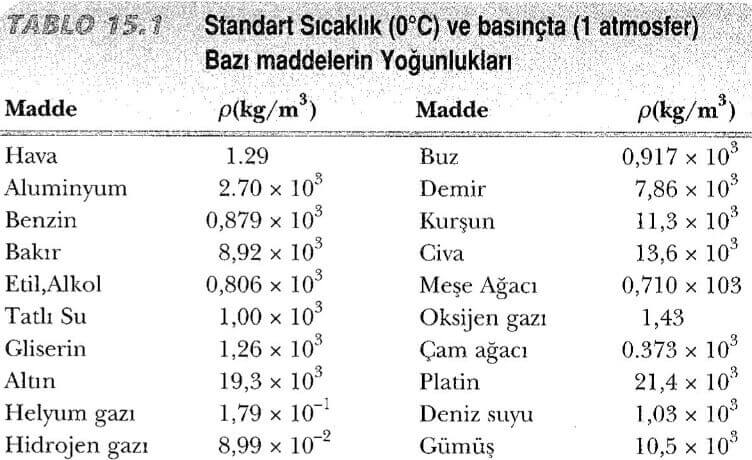
Şimdi bir sıvı içindeki basıncın derinlikle lineer olarak nasıl arttığını gö­relim. Bir maddenin yoğunluğu, birim hacminin kütlesi, yani ρ = m/V olarak tanımlanır. Çizelge 15.1, çeşitli maddelerin yoğunluk­larını gösteriyor. Bu değerler sıcaklıkla biraz değişir, çünkü bir maddenin hac­mi sıcaklığa bağlıdır. Standart koşullar altında (0°C ve 1 at­mosfer basınçta) gazların yoğunluğu, katılar ve sıvıların yoğunluklarının yak­laşık 1/1000 i olduğuna dikkat ediniz. Normal koşullar altındaki bir gazın, moleküller arası ortalama uzaklığını ima eden bu fark, katı ve sıvıdakinden yaklaşık 10 kez daha büyüktür.

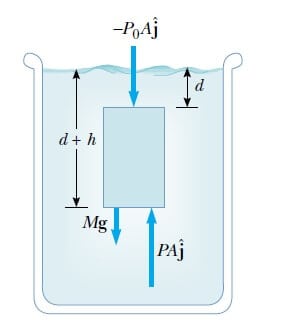
Şekil 4’de görüldüğü gibi, şimdi durgun haldeki yoğunluğu ρ ve üst yü­zeyi atmosfere açık olan bir akışkanı ele alalım. ρ nun sabit olduğunu varsaya­lım. Bunun anlamı, sıvının sıkıştırılamaz olmasıdır. Yüzeyden h derinliğine uzanan ve A kesitli sanal bir silindirle sınırlandırılan bir sıvı örneğini seçelim.

Silindirin taban yüzeyine dıştaki sıvı tarafından uygulanan basınç P ve üst yüzeyindeki basınç da atmosfer basıncı Po’dır. Böylece, silindirin taban yüze­yine dıştaki sıvı tarafından yukarıya doğru uygulanan kuvvet PA ve üst yüzeyine atmosfer tarafından aşağı doğru uygulanan kuvvet ise P₀A olur. Silindirde­ki sıvının kütlesi M = ρV = ρAh olduğundan silindirdeki sıvının ağırlığı Mg = ρAhg şeklinde yazılır. Silindir dengede olduğuna göre ona etki eden net kuv­vet sıfır olmalıdır. Pozitif y yönünü yukarıya doğru seçelim. Bu durumda den­ge koşulu,

yada

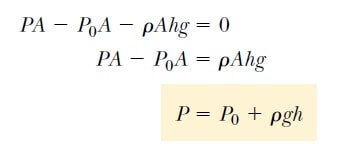
olur. Yani, üst yüzeyi atmosfere açık olan bir sıvının h derinliğindeki  P basın­cı, atmosfer
basıncından basıncın derinlikle değişimi ρgh miktarı kadar büyük­tür. Hesaplamalarda ve problemlerin çözümünde atmosfer basıncı,

P₀ = 1 atm = 1,013 x 10⁵ Pa

olarak alınır. Eşitlik 4, aynı yüksekliğe sahip olan bütün noktalardaki basın­cın aynı olduğunu ve kabın şeklinden etkilenmediğini ifade eder.

Sıvı içindeki basınç, yalnız sıvının derinliğine ve P₀ ın değerine bağlı olduğundan, sıvının yüzeyindeki basınca yapılan herhangi bir artış, sıvının diğer bütün noktalarına aynen iletilmelidir. Bu ilke, ilk kez Fransız bilgini Blaise Pascal (1623-1662) tarafından bulundu ve Pascal Yasası olarak adlandırıldı. Bir akışkana uygulanan basınçtaki bir değişiklik akışkanın her noktasına ve ka­bın duvarlarına değişmeksizin aynen iletilir.

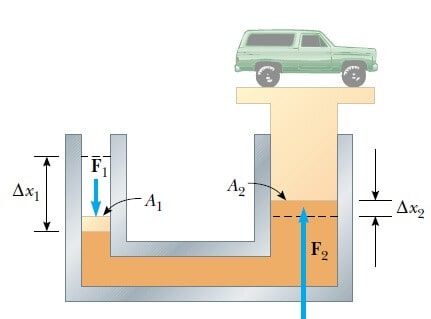
Pascal yasasının önemli bir uygulaması, Şekil 5’de gösterilen su cende­residir. Büyüklüğü F₁ olan bir kuvvet, yüzölçümü A₁ olan küçük bir pistona uy­gulanmaktadır. Basınç, akışkan tarafından yüzölçümü A₂ olan daha büyük bir pistona iletilmektedir. Her iki tarafta da basınç aynı olduğu için P =F₁/A₁ =F₂/A₂ yazılır. Boylece; F₂ kuvveti, F₁ kuvvetinden kuvvet-çarpma faktörü denilen A₂/A_l çarpanı kadar daha büyüktür. Akışkana ekleme ve çıkarma yapılmadı­ğından sol taraftaki pistonun d₁ kadar aşağı hareket etmesiyle aşağıya itilen akışkan hacminin, sağ taraftaki pistonun da d₂ kadar yukarı hareket etmesiyle yukarıya itilen akışkan hacmine eşit olmalıdır. Yani A₁d₁ = A₂ d₂ yazılır. Bura­dan kuvvet-çarpma faktörü d₁/d₂ şeklinde de yazılabilir. F₁d₁= F₂d₂ olduğuna da dikkat ediniz. Hidrolik frenler, araba asansörleri, hidrolik krikolar, çatallı kal­dırıcılar gibi aygıtlar bu ilkeyi kullanır.