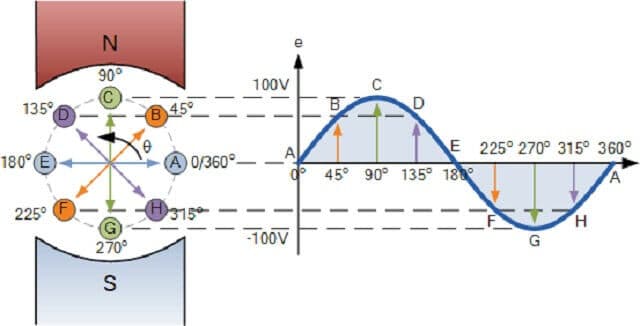
Bu yazımızda, biçimi şekil 1’de görülen önemli bir dalga fonksiyonunu ele alacağız. Bu eğriyle temsil edilen dalga, sinüssel dalgalar adını alır. Çünkü eğri, sinθ fonksiyonunun θ’ya göre çizimine benzer. Sinüssel dalgalar, periyodik ve sürekli dalganın basit bir örneğini oluşturur ve daha karışık dalgaların oluşturulmasında kullanılabilir. Kırmızı eğri, ilerleyen dalganın t = 0 anındaki durumunu, mavi eğri ise t süre sonraki durumunu gösterir. Sinüssel dalganın içinden geçtiği ortamın parçacığın t = 0 da, konumunu belirleyen fonksiyon aşağıdaki gibi yazılabilir.
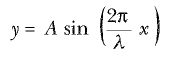
şeklinde yazılır. Burada A sabitine dalganın genliği denir ve maksimum yer degiştermeyi gösterir. λ sabiti, dalga boyu adını alır ve iki ardışık maksimum, yani dalga tepeleri arasındaki ya da aynı fazdaki iki komşu nokta arasındaki uzaklığa eşittir. O halde, x, λ nın tam katlan olacak şekilde artarsa, yer değiştirmenin kendisini tekrar ettiğini görürüz. Dalga, v hızı ile sağa doğru hareket ederse, t süre sonra dalga fonksiyonu,
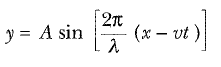
şeklinde olur. Yani; Şekil 1’de görüldüğü gibi, sinüssel dalga t süresi içinde vt uzaklığı kadar sağa hareket eder. Dalga fonksiyonunun f(x- vt) biçiminde olduğuna ve sağa doğru ilerleyen bir dalgayı gösterdiğine dikkat ediniz. Dalga sola doğru ilerlerse, x-vt yerine x + vt niceliği gelecektir.
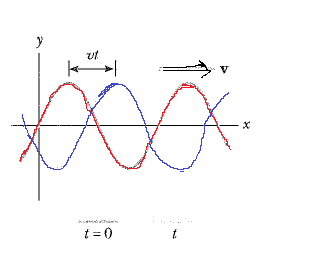
Şekil 1 Sağa doğru v hızı ile ilerleyen bir-boyutlu sinüssel dalga. Kırmızı eğri; dalganın t = 0 anındaki durumunu, mavi eğri ise t zaman sonraki durumunu gösterir.
Dalganın, bir dalga boyu kadar bir mesafeyi alması için geçen süreye T periyodu denir. Bu nedenle; dalga hızı, dalga boyu ve periyod arasında,
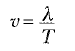
bağıntısı vardır. Bu, (1) Eşitliğinde yerine konursa;
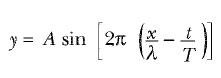
bulunur. Dalga fonksiyonunun bu biçimi açıkça, у nin periyodik olduğunu gösterir. Yani, verilen herhangi bir t anında (dalganın bir andaki durumu) x, x+ λ , x+ 2λ vb. konumlarında, у aynı değerde olur. Dahası, verilen herhangi bir x konumunda у nin değeri t, t + T, t+2T vb. zamanlarda da aynı olur.
Sinüssel dalga fonksiyonunu, başka iki nicelik tanımlayarak daha uygun bir biçimde ifade edebiliriz. Bu nicelikler, k açısal dalga sayısı ve açısal frekansıdır:

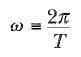
Bu tanımlar kullanılarak (2) Eşitliği daha basit bir biçimde yeniden şöyle yazılabilir:
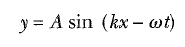
olur. Bu ifadeyi daha sık kullanacağız.
Bir sinüssel dalganın frekansı, saniyede, sabit bir noktadan geçen bir dalga tepesinin (ya da dalganın herhangi bir noktasının) sayısına eşittir. Frekans, periyoda aşağıdaki bağıntı ile bağlıdır:
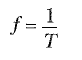
f nin çok kullanılan birimi s-1 ya da hertz (Hz) dır. T nin birimi ise saniye (s) dır.
(3), (4) ve (6) Eşitliklerini kullanarak, Eşitlik 1-1 de verilen v dalga hızını aşağıdaki gibi değişik biçimlerde ifade edebiliriz:
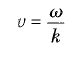
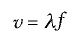
(5) Eşitliği ile verilen dalga fonksiyonu, x = 0 ve t = 0 da у yerdeğiştirmesinin sıfır olduğunu ifade eder. Bunun her zaman böyle olması gerekmez. x= 0 ve t = 0 da enine yer değiştirme sıfır değilse, genellikle dalga fonksiyonunu aşağıdaki biçimde ifade ederiz:
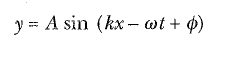
Sinüssel Dalgalar İle İlgili Örnek
İlerleyen Sinüssel Dalgalar
Pozitif x yönünde ilerleyen sınüsscl bir dalganın genliği 15 cm, dalgaboyu 40 cm ve frekansı 8 Hz dir. x = 0 ve t = 0 anında dalganın yer değiştirmesi, Şekil 2 de görüldüğü gibi, 15 cm dir. (a) Dalganın k dalga sayısını, T periyodunu ω açısal frekansını, v hızını bulunuz.
Çözüm:3, 4, 6, 7 Eşitliklerini kullanarak;
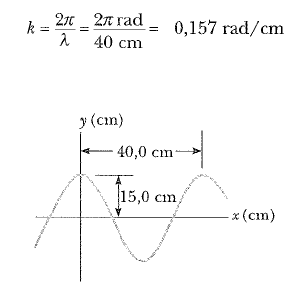
Şekil 2 Bir sinüssel dalganın dalga boyu X = 40cm ve genliği A = 15cm dir. Dalga fonksiyonu, у = A cos(kx – ωt) biçiminde yazılabilir.
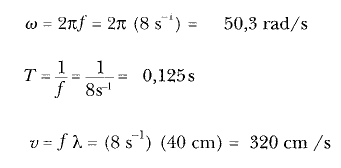
(b) ф faz sabitini bularak, dalga fonksiyonunun genel ifadesini yazınız
Çözüm:Genlik A = 15 cm ve x = 0, t = 0 da у = 15 cm
kullanılırsa;
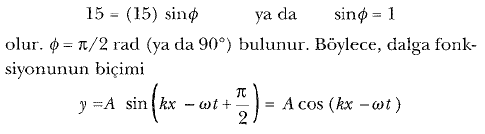
olur. Bu, kosinüsün argümanının, sinüs fonksiyonundan 90° farklı olduğuna dikkat edilerek görülebilir. A, k, ve ω nın değerleri bu ifadede yerine konursa,
у = (15 cm) cos(0,157x-50,3t)
elde edilir.