Şimdiye kadar öğrendiklerimizle, denetleyiciyi kapalı çevrimli (closed-loop) bir simülasyonda test etmek ve ince ayar yapmak için gerçek bir otomobilin basit bir matematiksel modelini yapmaya hazırsınız. (Bir önceki makaleyi okumanızı tavsiye ederim) Neyseki günümüzde neredeyse her araba için çok fazla teknik ayrıntı mevcut. Bizde bu teknik dökümanlardaki bilgileri kullanarak Alfa Romeo 147 GTA‘yı modelleyeceğiz. Yeni bir Simulink modeli açın ve alfa147gta.slx olarak kaydedin. Model bir girişe (gaz kelebeği, cruise kontrolöründen geliyor) ve bir çıkışa (otomobilin hızı, cruise kontrolörüne gidiyor) sahip olacak.
Bu problemimizi sadece eksenel hızla (Vx) giden (düz bir zeminde) araç için ilgileniyoruz ve dişli kutusunun ideal olduğunu düşünüyoruz (kısa sürede vites değiştiriyoruz). Şimdi, hızı nasıl hesaplayabiliriz?
Hız Hesabı – Newton kanunları
Aracın hızının zaman içindeki ivmenin ayrılmaz bir parçası olduğunu biliyoruz:
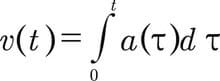
Newton’un ikinci yasası, ivmenin aracın üzerine uygulanan toplam kuvvetle orantılı olduğunu ve kütle faktörünün olduğunu hatırlatıyor:
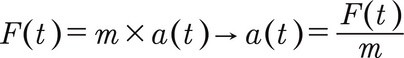
Basitleştirilmiş bir model oluşturduğumuzdan, yalnızca aşağıdaki üç ana kuvveti göz önüne alacağız:
- Motordaki yakıtın yanması sonucu ortaya çıkan, motor gücü: Fengine
- Hava içerisinde hareket eden (viskoz bir akışkanda) araba tarafından üretilen, aerodinamik sürüklenme: Fdrag,
- Harekete karşı gelen tüm sürtünme sürtünmelerinin toplamı, yuvarlanma direnci: Fres
Hepsini bir araya getirirsek:
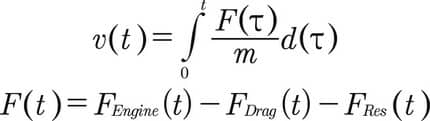
Kütle sabittir, bunu hemen çalışma alanına bildirebiliriz. Alfa 147 GTA 1360 kg ağırlığındadır, bu nedenle aşağıdaki komutu MATLAB ana penceresine girelim:
Mass = 1360;
İlgili blokları kök sisteminde (root system) oluşturalım. Library Browser‘ı açın ve Ports & Subsystems blok setinden modele üç Subsystem (altsistem) bloğu sürükleyin (uygulanan her kuvvet için bir tane olmak üzere); Math Operations blok setinden bir add blok ve bir Divide bloğu ekleyin; Continuous bloksetten bir Integrator bloğu; ve kütle için kaynaklardan (Sources blockset) bir Constant bloğu ekleyelim.
Bu model içerisinde uluslararası metrik sistemi ile çalışacağımız için, hız birimini m/s’den seyir kontrolör birimi km/h’e dönüştürmek için çıktıdan önce bir Kazanç bloğunu (Gain block) (Math Operations blok setinden) koyacağız.
Subsystem bloklarını Aerodinamik sürüklenme (Aerodynamic drag), Yuvarlanma Direnci (Rolling Resistance) ve Motor Gücü (Engine Force) olarak yeniden adlandırın ve onları dikey olarak hizalayın.
Blok ekle (Add block) üzerine çift tıklayın ve işaretler listesini düzenleyin; Üç girişe ihtiyacımız var, sadece bir tanesi pozitif (motor gücü). Pozitif girdiyi sonda tutalım; İşaretlerin listesi – – + olmalıdır. Sabit bloğuna (Constant block) çift tıklayın ve Sabit değer parametresini Kütle’ye (yalnızca çalışma alanında oluşturduğumuz değişken) ayarlayın.
Aynısı kazanç bloğu (Gain block) için de yapılmalıdır ve m/s’den km/h’ya dönüştürmek için Kazanç değerini 3.6 olarak ayarlayın.
Kısa bir not düştükten sonra, yukarıdaki formülleri izleyen blokları birbirine bağlayarak ve blokları yeniden adlandırdıktan sonra, aşağıdaki ekran görüntüsünde bir modele sahip olmalıyız:
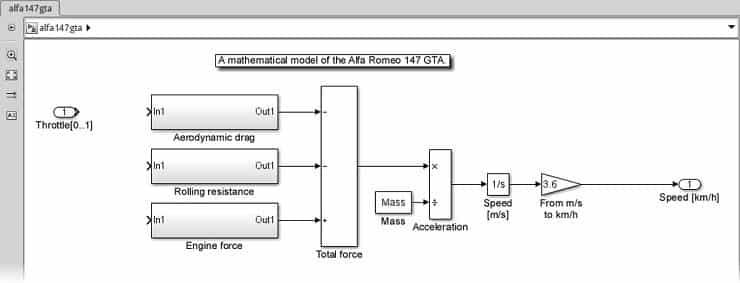
Hala kuvvetleri hesaplamamız gerekiyor. Basit sürtünme ve yuvarlanma direnci ile başlayacağız; çünkü bunlar daha basit! O zaman motor kuvvetini hesaplayan algoritmayı oluşturalım.
Aerodinamik sürüklenme denklemi
Yüksek araç hızlarında etkisi belirgin olan sürtünme kuvveti denklemi şu şekilde hesaplanabilir:
![]()
Kdrag, aşağıdaki koşullarda sabit bir sayıdır:
- Ön cephe alanı A, yaklaşık 2,2 m2‘dir. (Katalogdan)
- Hava yoğunluğu ρ, 20°C ve 101.325 kPa’da 1.2041 kg/m3‘e eşittir
- Sürükleme katsayısı Cd, 147 GTA için 0.32’dir. (Teknik katalogdan)
Bunu aşağıdaki komutu kullanarak çalışma alanına bildirelim:
Kdrag = 0.5 * 1.2041 * 0.32 * 2.2;
Araç hızının bir giriş bloğu (input) olması gerektiği için, Signal Routing blok setinden kök bloğa Goto ve From bloğu ekliyoruz.
Her ikisini açın ve aynı etiketi kullanın: hız (speed). Adlarını gizlemeniz önerilir! Goto bloğunu integratörün sonuna bağlamaya özen gösterin. Hızı km/h olarak değil, m/s cinsinden istiyoruz. Kök sistem, aşağıdaki ekran görüntüsü gibi görünmelidir:
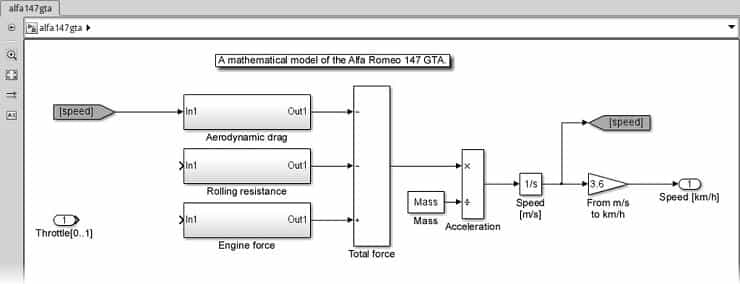
Aerodinamik sürüklenme (Aerodynamic drag) alt sistemi içerisinde, sürtünme denklemini bir Kazanç bloğu (Gain block), bir Matematik fonksiyon bloğu (her ikiside Simulink | Math İşlemleri’nden) ve bir Sabit bloğu (Constant block) (Simulink | Sources) ile uygulayacağız.
Kdrag‘ı Kazanç bloğu (Gain block) için bir Kazanç parametresi olarak kullanacağız ve Math fonksiyon bloğundaki pow fonksiyonunu seçeceğiz (çift tıklayın ve açılan fonksiyon listesinden pow konumuna getirelim). İkinci bir girdi (input) görünecek; üstel (exponential) olarak uygulamak için; Onu Constant bloğuna bağlayıp Constant değer parametresini 2 olarak ayarlayacağız.
Son olarak, giriş ve çıkış bağlantı noktalarını yeniden adlandırıp bağlayacağız, girdi hızı (m/s cinsinden) ve çıkış (N cinsinden) sürükleme kuvvetidir. Bağlantıları yaptıktan sonra, alt sistem aşağıdaki gibi görünmelidir:

Temel sistemdeki hızı Goto giriş bağlantı noktasına kopyalayıp bağlamayı unutmayın! Bir sonraki adım olan yuvarlanma direncini yapalım.
Yuvarlanma direnci yaklaşımı
Yuvarlanma direnci (bazen yuvarlanma sürtünmesi veya yuvarlanma sürüklenmesi olarak adlandırılır) araç hızı ile orantılıdır. Daha düşük bir hızda ana direnç budur.
Doğru bir formül elde etmek basit değildir, çünkü lastik özellikleri hakkında bilgilerde bu formülde yer almalıdır, ancak şunu varsayarak hesaplamaları basitleştirebiliriz:
- Yaklaşık olarak 30 m/s’de (100 km/h) yuvarlanma direnci ve sürüklenmesine eşittir.
- Orantısal faktör (proportional factor) diğer hızlarda sabittir.
Bu varsayım çoğu araba için geçerlidir. Bu nedenle, v = 30 m/s ile sabit KRes‘i bulabiliriz:
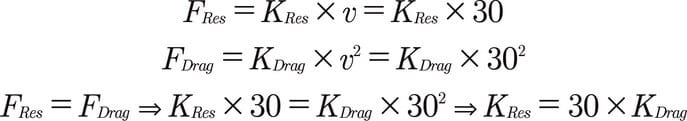
KRes tam olarak Kdrag‘dan 30 kat daha büyüktür, çalışma alanında yeni bir değişken bildirmek zorunda bile değiliz.
Uygulama basit: Yuvarlanma direnci (Rolling resistance) alt sistemi içerisinde, kazanç bloğunu 30*Kdrag olarak ayarladık ve bunları giriş ve çıkış bağlantı noktalarına (her zamanki gibi yeniden adlandırıldı) bağladık. Bu şekilde bir alt sisteme sahip olmalıyız:
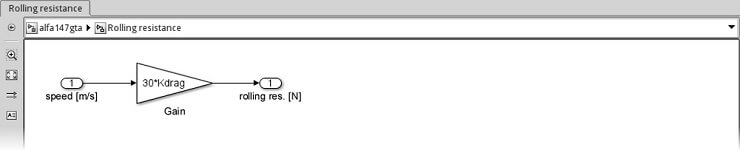
Temel sistemdeki hızı Goto giriş bağlantı noktasına kopyalayıp bağlamayı unutmayın! Şimdi zor kısma geliyoruz: cruise kontrolörü tarafından istenen motor gücünü hesaplayan alt sistem hesabı (gaz kelebeği girişi üzerinden)!
Motor gücü – motor, tekerlekler ve şanzıman
Her yanmalı motor, hemen hemen her teknik inceleme kitabında bulunabilecek karakteristik bir tork eğrisine (lug curve olarak da bilinir) sahiptir. Alfa 147 GTA için aşağıdakileri göstermektedir:
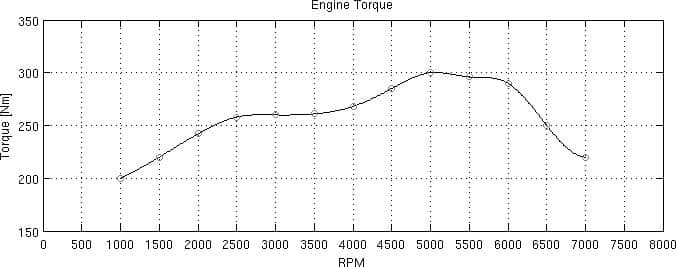
Grafikte, krank mili üzerinde ölçülen maksimum torku τmax (gaz kelebeği tamamen açıkken) göstermektedir. Motor ve tekerlekler, şanzıman ve diferansiyel aracılığıyla birbirine bağlanır; önce değişken bir dişli oranı KGear , sonra sabit bir final oranı KFinal uygulanır.
Önce aracın hızını motor devrine (rpm) ve son olarak da motor torkunu motor gücüne çevirmek zorunda olduğumuz için şanzıman ve diferansiyel karma oranlarının hepsini hesaba katarak dikkate almamız, dört alt sistem olarak modellememiz gereklidir:
- Şanzıman ve diferansiyel, aktarım oranını (transmission ratio) mevcut hızda çıkış (output) olacak.
- Tekerlerden motor devrine (rpm) dönüşüm – Wheel to RPM, mevcut aktarma oranı ve mevcut hız temel alınarak mevcut RPM output (çıkış) olacak.
- Motor, gaz kelebeği komutunu alacak ve elde edilen torku şu anki RPM’de output (çıkış) olacak
- Torktan kuvvete dönüşüm – Torque to force, motor torkunu motorun arabaya uyguladığı kuvvete dönüştürecek.
Motor Kuvveti (Engine force) alt sisteminde iki giriş (input) portu (araç hızı ve gaz kelebeği girişi), bir çıkış (output) portu (motor kuvveti) ve dört boş Subsystem bloğu (Simulink | Ports & Subsystems’de bulunur) ile başlayalım. Alt sistem aşağıdaki ekran görüntüsüne benzetilmelidir:
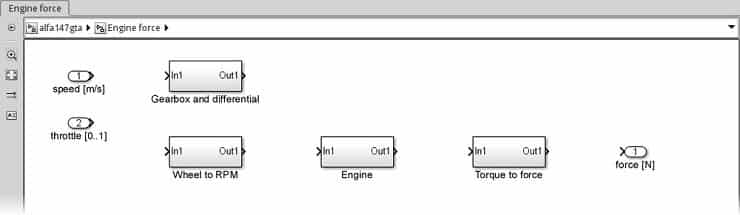
Uygulayacağımız ilk alt sistem Şanzıman ve diferansiyeldir.
Vites Kutusu ve Diferansiyel
Krank milinden tekerleğe olan dönüş (rotation) iki kere azaltılır: ilkini redüktörde vites büyütme/küçültme ile, diğerini ise sabit redüksiyon oranı olan diferansiyelde değiştirilebilir.
Otomatik şanzıman uygulamamız lazım; En kolay olanı, mevcut hızı temel alan ve geri vitese sahip olmayan dişli kutusu seçimidir.
Aşağıdaki tabloda, Alfa 147 GTA‘nın her dişli için en uygun hız aralıklarını dişli oranı KGear ile birlikte bulacağız:
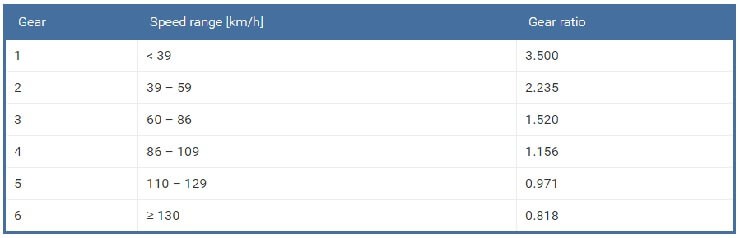
Alfa 147 GTA’daki diferansiyel, 3.733’lük bir son oran (KFinal) uygulamaktadır.
Örnek olarak: birinci viteste, motorun krank mili, tekerlek ekseninden 13 kat (3.5 * 3.733) daha hızlıdır. Altıncı viteste ise sadece üç kat daha hızlı (0.818 * 3.733) dönmektedir.
Bu verileri aşağıdaki komutları uygulayarak çalışma alanına koyacağız:
GearRatio = [3.500 2.235 1.520 1.156 0.971 0.818];
FinalRatio = 3.733;
Otomatik şanzıman yapalım; Giriş, m/s cinsinden araç hızı olup, değeri 3.6 olarak ayarlanmış bir Kazanç bloğu (Gain block) aracılığıyla km/h’e dönüştürülür.
Sonra dişli kutusunu seçmek için Ports & Subsystems blok setinden bir If bloğunu kullanacağız. If bloğu, C dilinin if () … elseif () … else yapısını tam olarak çoğaltmamızı sağlar. Blok parametreleri penceresini açtığınızda, ilk if() koşulunu ayarlamamız gerektiği ortaya çıkar: istediğiniz kadar çok sayıda elseif() koşulunu tanımlayabiliriz.
Hız aralıklarına baktığınızda parametrelerin ayarlanması kolaydır:
- Girişlerin sayısı 1’e ayarlanacaktır, zira sadece araç hızını değerlendirmeliyiz (blok içindeki ilgili etiket u1 olacaktır)
- If ifadesi u1 <39 olacak (birinci vites)
- Elseif ifadesinin elemanları u1 <60, u1 <86, u1 <110, u1 <130 olacaktır (vites 2 ile 5 arası)
- Else durumunu göster onay kutusu işaretlenecek (altıncı vites)
Parametreleri doğru girdiysek şu an aşağıdaki alt sisteme sahip olmalıyız:

If bloğunun her çıkışı için bir (If Action Subsystem) Eylem Alt Sistemini (Ports & Subsystems blok setinde bulunur) koymamız gerekir. Bu alt sistemler, If bloğundaki ilgili koşul doğrulanmış (ki buna koşullu yürütülen alt sistemler denir) yürütülecek kodu içermelidir. Bizim durumumuzda, seçilen vites numarasını çıkartacaklardır (output edecektir). Giriş bağlantı noktasına ihtiyacımız yok; Bunun yerine dişli sayısı olan Sabit bir blok (Constant block) kullanarak bu alt sistemlerin her birinden çıkarın.
Aşağıdaki ekran görüntüsünde, alt sistemin ilk vitese göre (If Action Subsystem) İf Eylem Alt Sistemi’ni ekleyip düzenledikten sonra Simülasyon | Diyagram eylemini güncelle/Update Diagram action veya (klavye kısayolu Ctrl + D‘dir) komutunu çalıştırın:
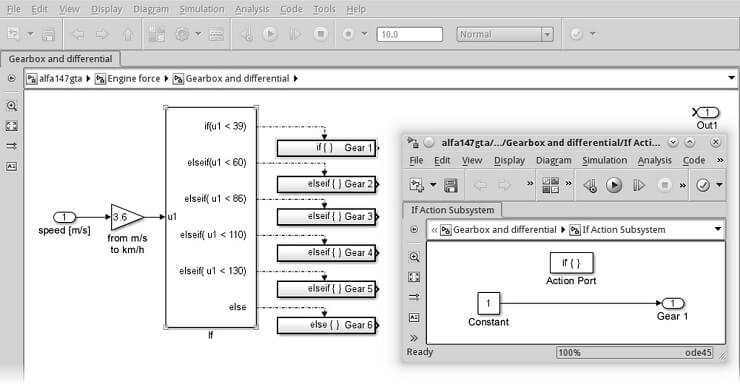
If bloğu ile alt sistemler arasındaki bağlantıların noktalı olduğuna dikkat edin. Bu, bağlantının bir sinyal nakletmediği anlamına gelir, ancak bir fonksiyon çağrısıdır. Bir durum doğrulandığında, If bloğu ilgili porta bağlanan alt sistemi arar, kodunu çalıştırır.
Simulink’in MATLAB’ın ana penceresinde uyarı vermesini önlemek için koşullu olarak çalıştırılan her alt sistemin çıkış bağlantı noktaları, parametreler penceresinde başlangıç çıkış değerlerini ayarlamalıdır.
Şu anda altı olası dişli değeri var; Onları nasıl bir araya getirebilirim? Başka bir özel blok kullanmalıyız: Sinyal Yönlendirme (Signal Routing) blok setinden Birleştirme (Merge) bloğu! Bu blok, bağlı alt sistemleri çıkışlarını aynı sinyale yazmaları için talimatlar verir.
Modelimize bir Merge bloğu yerleştirelim ve parametreler penceresini çift tıklatarak açalım. Altı alt sistemimiz olduğundan, Number of inputs parametresini 6‘ya ayarlamalı ve daha sonra her alt sistemi girişlerden birine bağlamalıyız.
Elde edilen model şu şekilde olmalıdır:
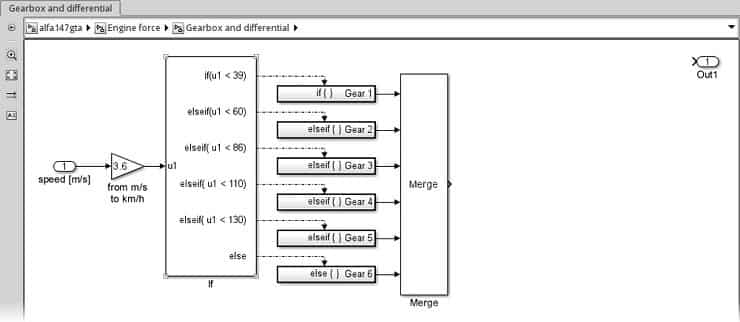
Artık şimdi vites sistemine sahibiz, dişli oranını seçmek için bunu kullanmalıyız.
Direct Lookup Table – Doğrudan Arama Tablosu (n-D) (Simulink | Arama Tablolarından – Lookup Tables) kullanacağız. Parametreler penceresini açın, Tablo boyutlarının sayısını 1‘e, Tablo verisi (Table data) parametresini GearRatio‘ya ayarlayın. Tablonun sıfır tabanlı bir dizinle (zero-based index) erişilmesi gerektiğinden Merge bloğundan gelen dişli sayısından bir birim çıkarmalıyız.
Alt sistem ve Doğrudan Arama Tablosu (Direct Lookup Table) parametreleri aşağıdaki ekran görüntüsünde gösterilmektedir:
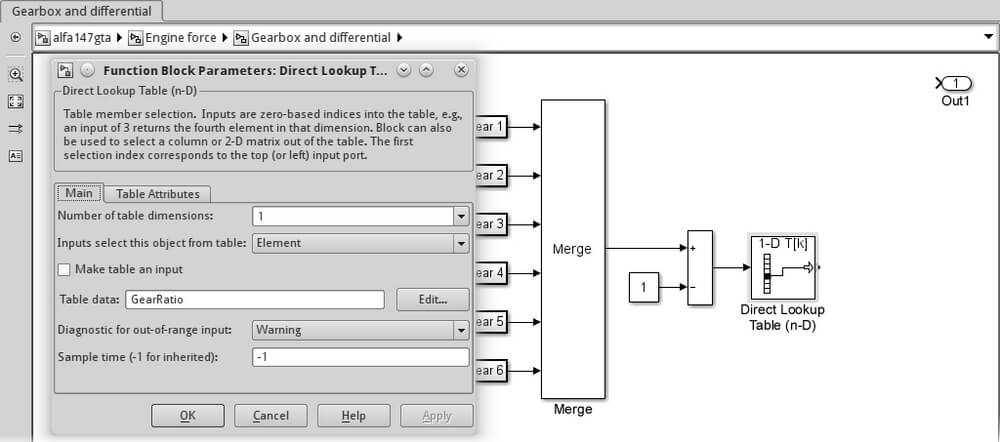
Son adım, diferansiyel nedeniyle son oranı (final ratio) içermektir. Bu, Kazanç bloğunu (Gain block) çıkış bağlantı noktasının hemen önüne koyarak (yeniden adlandırılması gerekir) ve Kazanç parametresini FinalRatio olarak ayarlayarak kolayca yapılır.
Nihai şanzıman ve diferansiyel alt sistemi aşağıdaki ekran görüntüsünde gösterilmektedir:
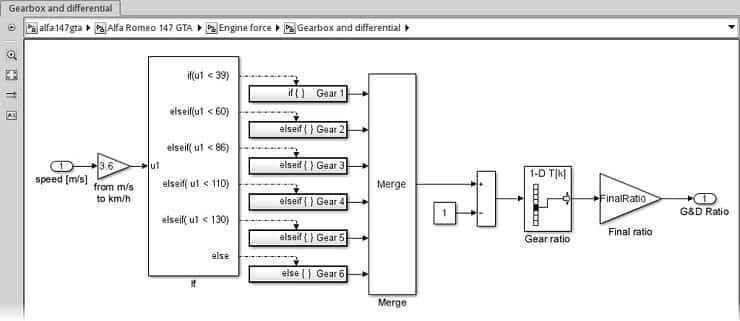
Bu alt sistemin çıktısı araç hızını motor devrine ve daha sonra motor torkunu yeni araç hızına dönüştürmek için kullanılacaktır.
Tekerlekten RPM’ye
Bu alt sistemin amacı iki giriş kullanarak motor devri elde etmektir: araç hızı ve kombine (dişli ve diferansiyel) redüksiyon oranı!
Araç hızı v tekerleğin dönüş hızına çevrilebilir (RPM, dakikadaki devir sayısı). RPMWheel, arabanın 60 saniye içinde seyahat ettiği mesafeye eşittir (v*60), tekerlek çapına bölünür (yani, tekerleğin yarıçapı rWheel‘in 2π katıdır).
Sonra, motorun ve tekerleklerin şanzıman ve diferansiyel yoluyla birbirine bağlandığını biliyoruz. Zaten oranlarına sahibiz; Motorun RPMEngine, dişli ve diferansiyel oranlarıyla çarpılarak elde edilen RPMWheel‘ye eşittir.
Bu bize Simulink’te uygulanacak kolay formülleri verir:
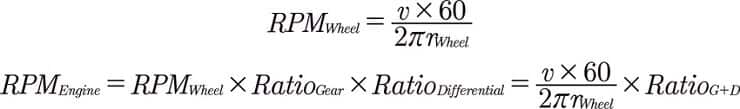
Alfa Romeo 147 GTA, 185/45R17 lastikleri kullanıyor, yani:
- Tekerlek jant çapı 17 in = 0.4318 m
- Lastik kesit yüksekliğinin 185 mm’nin %45 ≈ 83.3 mm
Tekerlek yarıçapı 0.4318 / 2 + 0.0833 = 0.2992 m. Bu komutu kullanarak çalışma alanına kaydedin:
WheelRadius = 0.2992;
Önceki formülün ardından Simulink’deki alt sistemin uygulanması, bilinen Kazanç (Gain), Böl (Divide) ve Ürün (Product) bloklarını kullanarak basittir:
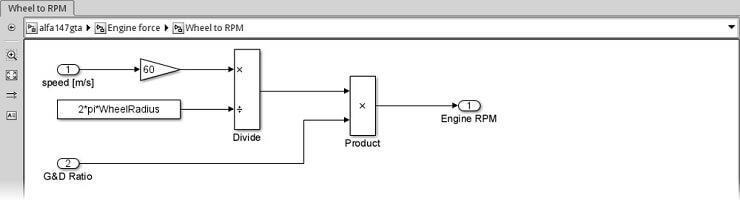
Artık motor devri var, Motor altsistemini modelleyebiliriz.
Motor
Bu alt sistem, motor torkunun tepkisini τEngine hesaplar. Girişler, önceki alt sistemden gelen motor devri ve cruise kontrol sistemindeki gaz kelebeği komutudur. Formülü çok basit:
![]()
Belirli bir devirde maksimum tork τMAX elde etmek için, aşağıdaki koordinatları kullanarak bir interpolasyon bloğuna ihtiyacımız var (bu bölümün önceki bölümlerinde gördüğümüz tork eğrisinden alınmıştır):
 Bu vektörleri çalışma alanına ekleyelim:
Bu vektörleri çalışma alanına ekleyelim:
EngineRPM = [1000 1500 2000 2500 3000 3500 4000 4500 5000 5500 6000 6500 7000];
EngineTRQ = [200 220 242 258 260 261 268 285 300 296 290 250 220];
Motor alt sistemine, 1 Boyutlu Arama Tablosu (1-D Lookup Table) (Simulink | Lookup Tables) yerleştirip, üzerine çift tıklayıp şu şekilde yapılandırılacağız:
- Tablo boyutları: 1 (her RPM değeri için yalnızca bir tork değerine ihtiyacımız var)
- Tablo verileri: EngineTRQ (ordinatlar)
- Breakpoints 1: EngineRPM (enlem kesitleri)
- Enterpolasyon yöntemi (Algoritma sekmesinde): Kübik spline – Cubic spline (bilinen iki nokta arasındaki eğri nasıl hesaplanır)
- Ekstrapolasyon yöntemi (Algoritma sekmesinde): Doğrusal – Linear (RPM aralığının dışındaki eğri nasıl hesaplanır)
Motor altsistemi uygulaması aşağıdaki ekran görüntüsüne benzeyecektir:
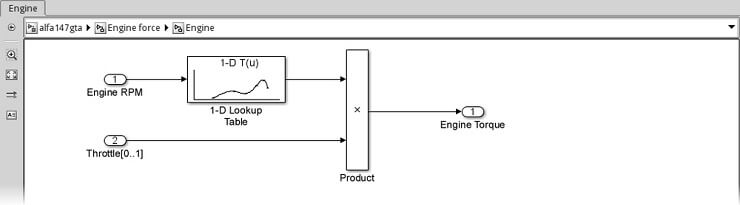
Kolay değil mi? Sonuçta elde edilen τEngine‘e sahip olduğumuza göre, motorun bir sonraki alt sistemdeki araca uyguladığı kuvveti hesaplayabiliyoruz.
Tork’tan Kuvvete
Bu alt sistem sağlanan motor torkunu τEngine‘i araca uygulanan F kuvvetine çevirir.
Newton’un üçüncü yasası sayesinde, aynı F kuvvetinin tekerlekler tarafından yere uygulandığını biliyoruz. Tork tanımını hatırlayarak, dişli ve diferansiyel oranlarını uygulayarak F’yi tekerlek torku τWheel ile diğeri motor torkuna ilişkilendirebiliriz:
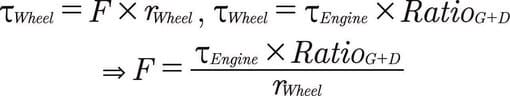
Yukarıdaki formülün Simulink uygulaması, aşağıdaki ekran görüntüsünde olduğu gibi, şimdi tanıdık Product, Divide ve Constant (WheelRadius olarak ayarlandı) bloklarıyla kolayca yapılır:
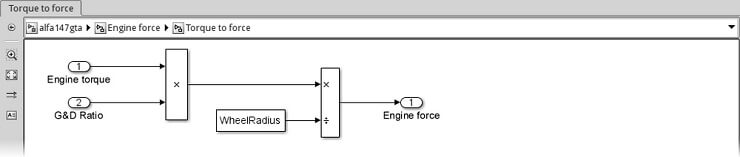
Her zamanki gibi, alt sistemlerde ilgili bağlantıları güncellemeyi unutmayın.
Son rötuşlar
Her şeyden önce, tüm kök-düzey alt sistemlerini (root-level subsystems) Alfa Romeo 147 GTA adlı bir alt sistemde gruplayalım ve ihtiyacımız olan her sabiti ilan ettiğimizden bu çalışma alanını alfa147gta.mat olarak kaydedin.
Cruise modelinde yaptığımız gibi, modelin PreLoadFcn geri çağrısını aşağıdaki gibi ayarlayarak çalışma alanını otomatik olarak yüklemesini sağlayabiliriz: load (‘alfa147gta.mat’)
Ardından, her şeyi doğru bir şekilde yapıp tamamlamadığımızı kontrol etmek için Simulation | Update Diagram (Ctrl + D) komutunu çalıştırırız. Ortaya çıkan kök alt sistemi aşağıdaki ekran görüntüsüne benzeyecektir:
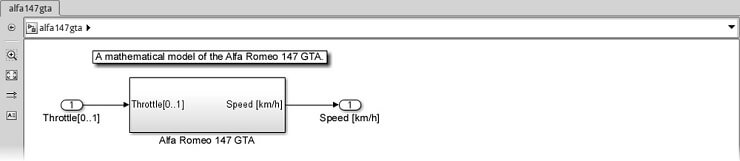
Bu kadar! Tamamen kullanışlı, oldukça doğru bir araba modeli yaratmayı başardık! Biz kontrolünü yaptığımız aracı sürümeyeceğiz belki ama kesinlikle model yarışlarında kullanabiliriz.
Kaynak: Getting Started with Simulink By Luca Zamboni

