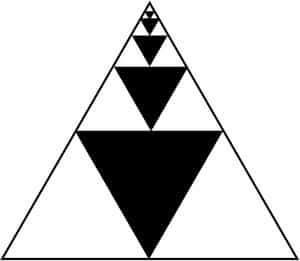
Matematikte serilerle ilgili çalışmalar yüzlerce yıldan beri hep merak konusu olmuştur. Aslında bunun temelinde yatan insanoğlunun sonsuzluk kavramı üzerindeki derin düşünüşleridir. Özellikle iç içe geçmiş şekillerin bir sarmal oluşturduğu geometrik şekillerin çevreleri, alanları, hacimleri birçok profesyonel matematikçi tarafından hesaplanmaya çalışılmış fakat birçok kez de başarısız olmuşlardır. Serilerin ilk çıkış noktası olan mantık ise “Altın Üçgenler” ismiyle anılan estetik bir objeden doğmuştur. Leibniz, Newton ya da Euler gibi matematikçiler bu konular üstünde çok derin çalışmışlardır. Aşağıda verilen şekli inceleyelim.
Şekilde üçgenlerin çevrelerinin toplamını bulabilmek için
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + ……
ifadesini hesaplamamız gerekmektedir. Bu ifadeyi lise bilgisi ile yapabilirsiniz ancak yukarıda da değimiz gibi bu ifadenin mantığını verelim. Sayı doğrusuna baktığımız zaman bu kesirlerin toplamını bulabiliriz. Seriye eklenen her kesrin serinin toplamını 1’e daha da yakınlaştırdığını göreceğiz ve hiçbir zaman da 1’i aşamayacağını anlarız. Böylece serinin toplamının 1 olduğunu anlarız. İşte ilk düşünce patlaması bu şekilde çıktı.
Şimdi bu şekillerin çevresi hakkında düşünelim. İlk üçgen için 30, diğeri için 15, sonra 15/2, 15/4, 15/8, 15/16…. şeklinde düşünebiliriz. Bunları toplayacağız… Hemen yazalım.
30 + 15 + 15/2 + 15/4 + 15/8 + 15/16 +15/32 + 15/64…….
Hemen ilk görünen şey 30+15 = 45 olduğu ve serinin toplamının 45’den büyük olduğudur. Size bir tavsiye; Tüm serileri 1/2 + 1/4 + 1/8 +1/16 + 1/32…. biçimine getirin. Yukarıda verilen,
15/2 + 15/4 + 15/8 + 15/16 +15/32 + 15/64…….
toplamını 15 parantezine alıp söylediğimiz ve sonucunun 1 olduğunu bildiğimiz seriye benzetebiliriz.
15.( 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + ……) = 15. 1 = 15
30 + 15 +15 =60 olacaktır.
Sonsuza giden bir şeklin çevresine bakar mısınız? Gözümüz korkmuştu.
Alanları ile ilgili toplama işlemi de farklı bir biçim alabilir. Yeni bir ıraksak seri (Toplamları sonsuza giden seriler diyelim ) tanımlayarak üzerinde çalışılabilir…