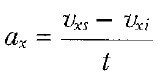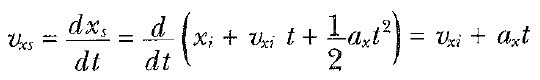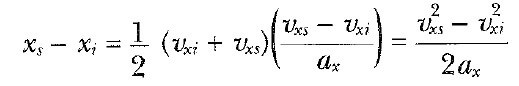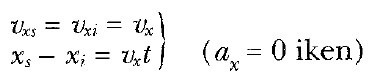Sabit İvmeli Hareket Konu Anlatımı

Merhaba arkadaşlar bu yazımızda sizlere sabit ivmeli hareket konu anlatımı yapacağız. Bir parçacığın ivmesi zamanla değişirse, hareketi, karmaşık ve analiz edilmesi zor olabilir. Fakat, bir-boyutlu hareketin çok genel ve basit bir tipi, ivmenin sabit veya düzgün olduğu durumdur, ivme sabit olduğunda, ortalama ivme ani ivmeye eşittir. Bu tür harekette hız, hareketin başından sonuna kadar aynı oranda artar veya azalır.

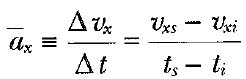
1 Eşitliğinde a_x(üzeri çizgili) yerine a_x koyarsak ve t_i = 0, daha sonraki t_s yerine de t alırsak

veya

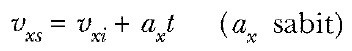
buluruz.

İvme Formülü

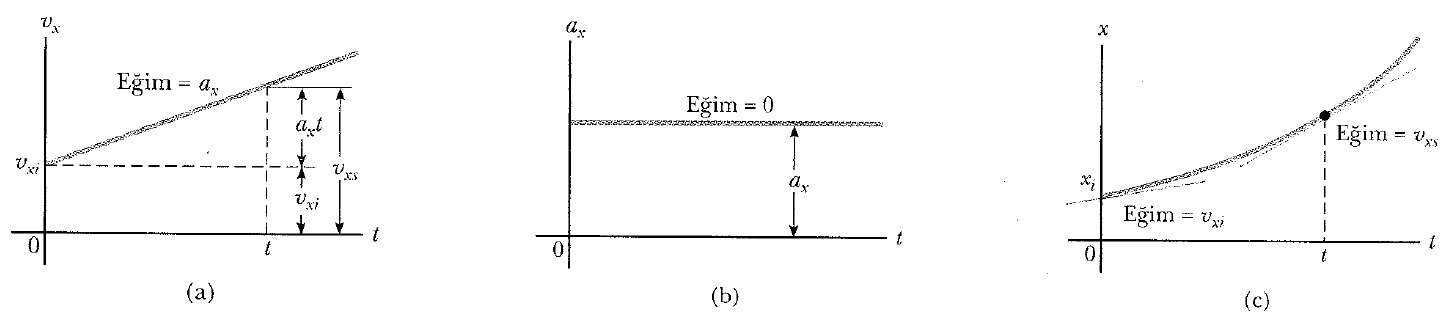
İlk hız, ve ivme (sabit) bilinirse, bu ifade yardımı ile herhangi orandaki hızı kolayca bulabiliriz. Sabit ivmeli hareket için hızın zamana göre grafiği Şekil 1a’da gösterilmiştir. Grafik, a_x = ∂v_x/∂t ‘nin sabit olması gerçeği ile uyumlu ve eğimi, a_x ivmesi olan bir doğrudur. Eğim, pozitiftir; Bu, ivmenin de pozitif olduğunu gösterir. İvme negatif olsaydı, Şekil 1a’daki çizginin eğimi de negatif olacaktı.

İvme sabit olduğunda, ivme-zaman grafiği (Şek.1b), eğimi sıfır olan bir doğru olur.

Şekil 1: Sabit a ivmesiyle x ekseni boyunca hareket eden bir parçacık; a) hız – grafiği b) ivme – zaman grafiği c) konum -zaman grafiği

2 Eşitliğine göre, hız zamanla doğrusal olarak değiştiğinden, herhangi bir zaman aralığındaki ortalama hız, v_xi ilk hızı ile v_xs son hızın aritmetik ortalaması olarak ifade edilebilir:

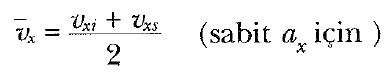
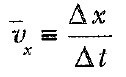
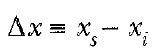
Bu ifadenin sadece, ivme sabit olduğu zaman uygulanabileceğine dikkat ediniz.

Şimdi 1.1, 1.2 ve 3 Eşitliklerini, yer değiştirmeyi zamanın fonksiyonu olarak elde etmek için kullanabiliriz. 2.2 Eşitliğindeki Δx’in x_s – x_i anlamına geldiğini anımsayarak (ilk anı t_i = 0 seçip) Δt yerine t alarak

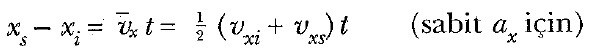
elde ederiz. 2 Eşitliğini 4 Eşitliğinde yerine koyarak, yer değiştirme için başka bir kullanışlı ifade elde edebiliriz:

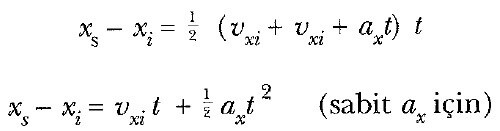
Şek. 1c’de gösterilen sabit (pozitif) ivmeli hareketin konum-zaman gra­fiği, 5 Eşitliğinden elde edilir. Eğri, bir paraboldür. Bu eğriye t = t_i = 0 nok­tasında çizilen teğetin eğimi, v_xi ilk hızına eşit olur. Daha sonraki bir t anında çizilen teğet doğrunun eğimi de, o andaki v_xs hızına eşit olur.

5 Eşitliğinin geçerliliği, zamana göre türevi alınarak kontrol edilebilir:

olur.

Son olarak, 2 Eşitliğinden elde edilen t değerini 4 Eşitliğinde yerine koyarak zamanı içermeyen bir ifade elde edebiliriz:

veya

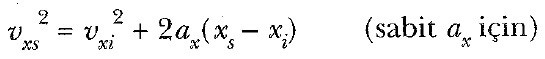
İvmenin sıfır olduğu bir hareket için, 2 ve 5 Eşitliklerinden

olur. Yani, ivme sıfır olduğu zaman hız sabittir ve yer değiştirme zamanla doğ­rusal olarak değişir.

Sabit İvmeli Hareket Özet

Eşitlik 2 den, 6 eşitliğine kadar olan denklemler, bir boyutta sabit ivmeli hareket ile ilgili herhangi bir problemi çözmek için kullanılabilen kinematik ifadedir. Bu bağıntıların bazı basit cebirsel işlemlerle birlikte, hız ve ivme ta­nımından türetildiklerini ve ivmenin sabit olması gerektiğini hatırlayınız.

En çok kullanılan dört kinematik eşitlik topluca Tablo 1’de listelenmiştir. Hangi kinematik eşitlik veya eşitliklerin kullanılacağı, eldeki mevcut bilgilere göre seçilir. Örneğin herhangi bir anda yer değiştirme ve hız gibi, iki bilinmeyeni çözmek için, bu eşitliklerin ikisini kullanmak zorunludur, v_xi ilk hızı ile a_x ivmesinin verildiğini kabul edelim: (1) bir t zamanı geçtikten sonra hızı, v_xs = v_xi + a_xt kullanarak, (2) bir t zamanı geçtikten sonra ivmeyi x_s – x_i = v_xit + 1/2 a_xt² kullanarak bulabilirsiniz. Hareket sırasında değişen nice­liklerin hız, yer değiştirme ve zaman olduğunu bilmelisiniz.

Çok sayıda alıştırma ve problem çözerek bu denklemlerin kullanımında önemli ölçüde deneyim kazanacaksınız. Çoğu zaman, bir çözüm elde etmek için birden fazla yöntemin var olduğunu keşfedeceksiniz. Kinematiğin bu eşit­liklerinin ivmenin zamanla değiştiği hareketlerde kullanılamayacağını unutmayınız. Bunlar sadece sabit ivmeli hareket için kullanılabilirler.