Merhaba sizlere roket hareketi ve roket hareketi denklemi bunun yanı sıra roket hareketlerini daha iyi kavramak için daha basit örneklerle sizlere anlatacağım. Otomobil, bot ve lokomotif gibi klasik araçlar itildiği zaman hareketin sürücü kuvveti sürtünme kuvvetidir. Otomobil hareketinde sürücü kuvvet, araba üzerine yolun uyguladığı kuvvettir. Bir lokomotif, rayları geri doğru “iter” ve böylece sürücü kuvvet lokomotif üzerine uygulanan ray kuvvetidir. Uzayda giden bir roketin geri iteceği hiçbir hava veya ray yoktur. O halde, roket itmesinin kaynağı farklı olmalıdır. Şekil 1, yerden fırlatılan bir uzay aracının tipik bir resmidir. Bir roketin çalışması, parçacıklar sisteminde olduğu üzere, momentumun korunumu kanununa dayanır, burada sistem, roket ve yaktığı yakıttır.

Bir roket hareketi, bir tekerlekli araba ile onun üstüne monte edilen makineli tüfeğin mekanik sistemi incelenerek daha iyi anlaşılabilir. Tüfek ateşlendiğinde, mermiler, bir doğrultuda mv momentumu kazanır, burada v hızı yere göre ölçülür. Ateşlenen her mermi için tüfek ve tekerlekli sistem zıt yönde dengeleyici bir momentum kazanır. Yani, merminin tüfek üzerindeki geri tepme kuvveti, tüfek ve sistemi ivmelendirir. Saniyede n tane mermi ateşlenirse tüfek üzerindeki ortalama kuvvet Fort = nmv olur.
Benzer şekilde, bir roket serbest uzayda (boşlukta) hareket ederken kütle, gaz olarak dışarı atılan kütle kadar eksildiği için momentumu değişir. Atılan gazlar momentum kazandığından, roket de zıt yönde dengeleyici bir momentum kazanır. Böylece roket, geri atılan gazların itmesi sonucu ivmelenir. Serbest uzayda, sistemin (roket artı çakan gazlar) kütle merkezi, itme kuvvetinden bağımsız olarak düzgün hareket eder.
Roket Hareketi Denklemi
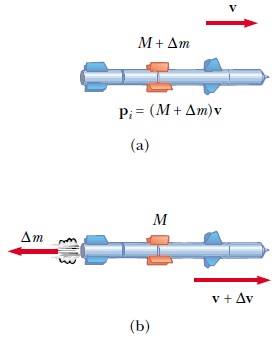
Her hangi bir t anında, roketle yakıtın momentumunun (M + Δm)v olduğunu farz ediniz v, roketin dünyaya göre hızıdır (Şekil 2a). Δt kadar kısa bir zaman sonra, roket Δm kütlesi kadar yakıt harcar ve roketin hızı v + Δv değerine ulaşır (Şekil 2b). Eğer yakıt, rokete göre ve (“e” indisi atılanları temsil eder ve ve’ye genellikle egzoz hızı denir) hızı ile atılırsa, yakıtın yere göre (durgun referans sistemi) hızı v — ve olur. O halde, sistemin ilk toplam momentumunu, son toplam momentumuna eşitlersek
(M + Δm)v = M(Δv+v) + Δm(v- ve)
elde ederiz; bunu sadeleştirerek aşağıdaki sonucu buluruz:
MΔv = veΔm
Bu sonuca, tüm sistemi, kütle merkezi referans sisteminde ele alarak da varabilirdik. Yani burada da sistemin hızı, kütle merkezinin hızı olarak alınır. Bu sistemde toplam momentum sıfırdır ve böylece roket bir miktar yakıt harcayarak MΔv momentumu kazanırsa, çıkan gazlar da zıt yönde bir veΔm momentumuna sahip olur ve sonuçta MΔv – veΔm = 0 olur. Δt → 0 limit durumunda Δv → dv ve Δm→ dm olur. Üstelik atılan kütledeki dm artışı, roket kütlesindeki azalmaya eşittir, yani dm = -dM. Kütle azalış gösterdiğinden dM negatif işaretlidir. Bu gerçeği kullanarak
Mdv = vedm = -vedm (eşitlik 1)
elde ederiz. Bu eşitliğin integralini alarak ve roket ile başlangıçtaki yakıt kütlesini Mi, kalan yakıtla birlikte roket kütlesini Mf alarak aşağıdaki sonucu elde ederiz:
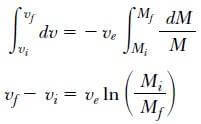
bu, roket hareketinin temel ifadesidir ve roketin hızındaki artış, yanan gaz hızı ile orantılı olmaktadır. O halde gaz çıkış hızı çok yüksek olmalıdır. Hızdaki artış ayrıca, Mi/Mf oranının logaritması ile de orantılıdır. O halde bu oran mümkün oldukça büyük olmalıdır, bu da mümkün olduğunca roketin çok yakıt taşıması gerektiğini ifade eder.
Roketi ileri iten etki (itici kuvvet), çıkan egzoz gazları tarafından rokete aktarılan kuvvettir. 1 Eşitliğinden itici kuvvet ifadesini elde edebiliriz:
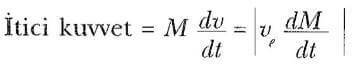
O halde itici kuvvet, çıkan gaz hızı ve kütle değişime hızı (yanma hızı da denir) arttıkça artar. Bu yazımızda roket hareketi hakkında bilgi verdik.


