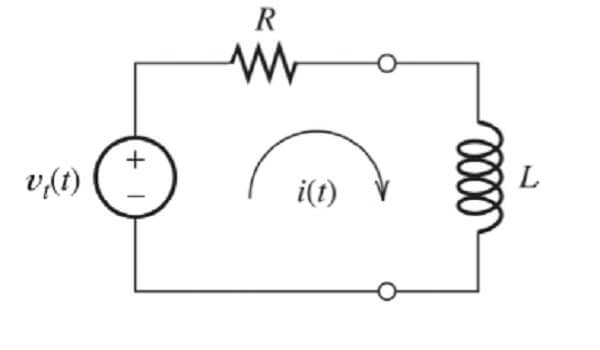
Bu yazımızda RL devresi nedir, RL devresi formüllerini anlatacağız ve konuyu daha iyi anlamak için RL devresi ile ilgili sorular çözeceğiz. Solenoid gibi, bir bobin içeren devre, akımın aniden artmasını veya azalmasını engelleyen bir öz indüksiyona sahiptir. Büyük indüktansa sahip bir devre elemanı indüktör olarak adlandırılır. Bir indüktörün devre sembolü;![]()
şeklindedir. Devrenin geri kalan kısmının öz indüktansını, indüktörün ki ile karşılaştırıldığında, ihmal edilebilir kabul edeceğiz.
Bununla birlikte, bir bobin içermeyen devrenin bile, devrenin davranışını etkileyebilecek, bir miktar öz indüksiyona sahip olduğu hatırda tutulmalıdır.
İndüktörün indüktansının bir ters emk’e neden olması yüzünden, devredeki bir indüktör, o devreden geçen akımın değişimine karşı koyar. Akımı artıracak şekilde devredeki batarya voltajı artırılırsa, indüktör, bu değişime karşı koyar ve meydana gelen artma aniden gerçekleşmez. Batarya voltajı azaltılırsa, indüktörün varlığı, akımda ani bir düşmenin yerine yavaş bir düşmenin gerçekleşmesine sebep olur. Böylece indüktör, akımdaki değişikliklere karşı koydukça devrenin daha yavaş davranmasına sebep olur.
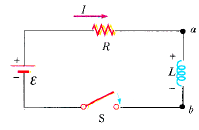
Şekil 1: Seri RL devresi. Akım, kendi maksimum değerine doğru arttıkça, indüktör, artan akıma karşı koyan bir emk üretir.
Bataryanın iç direncinin ihmal edildiği, Şekil 1’deki devreyi ele alalım. Bataryaya bağlanan elemanlar bir direnç ve bir indüktör olduğu için bu, bir RL devresidir. S anahtarının t = 0 da kapatıldığını varsayalım. Akım artmaya başlar ve indüktörde, artan akıma karşı koyan bir ters emk oluşur. Buna göre bu ters emk aşağıdaki bağıntı ile verilir:
![]()
Akım arttığı için dI/dt pozitiftir, dolayısı ile εL negatiftir. Bu negatif değer, indüktör boyunca a’dan b’ye doğru gidildikçe elektriksel potansiyelde bir düşüşün olduğunu gösterir; bu da Şekil 1 de pozitif ve negatif işaretlerle gösterilmiştir. Bunu akılda tutarak. Kirchhoff ‘un halka (ilmik) denklemini bu devreye, saat ibreleri yönünde dolanarak, uygulayabiliriz:
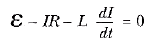
Buradaki IR direnç boyunca olan potansiyel düşmedir. (Doğru akımlı, devreler için Kirchhoff kurallarını türettik; fakat bu kuralları, zamanın belli bir anında devreyi temsil ettiklerini düşünerek, akımın değişmesi durumunda da uygulayabiliriz.) Şimdi bu diferansiyel denkleme, biçim bakımından DC devresine benzer, bir çözüm aramamız gerekir.
Eşitlik 1 in matematiksel bir çözümü, devredeki akımı, zamanın fonksiyonu olarak temsil eder. Bu çözümü bulabilmek için, kolaylık olsun diye![]()
olacak şekilde değişken değişimine gidilir. Bunları yerlerine yazarak Eşitlik 1 aşağıdaki şekilde yazılabilir:
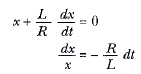
Bu son ifadenin integrali
![]()
sonucunu verir. Burada integral sabiti – lnx0 olarak alınmıştır ve t = 0 anındaki x ‘in değeridir. Bunun antilogaritması alınarak
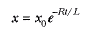 elde edilir, t = 0 da I = 0 olduğu için x ‘in tanımından x0 = ε/R olduğuna dikkat edilmelidir. Buradan, son ifade
elde edilir, t = 0 da I = 0 olduğu için x ‘in tanımından x0 = ε/R olduğuna dikkat edilmelidir. Buradan, son ifade
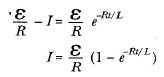
bağıntısına eşdeğerdir. Bu ifade, indüktörün etkisini göstermektedir. Anahtar kapatıldığı zaman, akım son denge değerine aniden artmaz; üstel bir fonksiyona uygun olarak artar. L yi sıfıra yaklaştırarak devredeki indüktansı kaldırırsak, üstel terim sıfır olur ve bu durumda akımın zamana bağlı olmadığım görürüz – indüktans yok iken akım, son denge değerine aniden artar.
Bu ifadeyi,
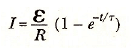
biçiminde de yazabiliriz. Burada τ sabiti RL devresinin zaman sabitidir:
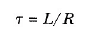
Fiziksel olarak т, akımın, son değer olan ε/R nin (1 -e-1) = 0,63 değerine ulaşması için geçen zamandır. Zaman sabiti, değişik devrelerin zaman bağımlılıklarını karşılaştırmada faydalı bir parametredir.
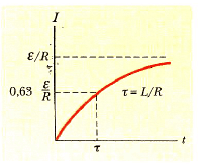
Şekil 2: Şekil 1 de görülen RL devresi için akımın zamana göre değişimi, t = 0 da anahtar kapatıldığında akım ε/R maksimum değerine doğru artar, t zaman sabiti, I nin maksimum değerinin % 63 üne ulaşması için geçen zamandır.
Şekil 2, RL devresindeki akımın zamana göre değişimini göstermektedir. t sonsuza yaklaştıkça akımın, son denge değeri olan ε/R ile verildiğine dikkat ediniz. Bu durum, Eşitlik 1 de dI/dt yi sıfıra eşitleyerek ve akıma göre çözerek görülebilir. (Denge halinde akımdaki değişim sıfırdır.) O halde akımın başlangıçta çok hızlı bir şekilde arttığını ve t sonsuza yaklaştıkça, ε/R denge değerine yavaş yavaş yaklaştığını görüyoruz.
Devredeki akımın zamana göre değişimini de inceleyelim. Denklem 32.7’nin zamana göre birinci türevini alarak aşağıdaki bağıntıyı elde ederiz:
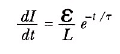
Bu sonuçtan, akımın zamana göre değişim oranının, t = 0 da maksimum (ε/L ‘ye eşit) olduğunu, t sonsuza yaklaştıkça üstel olarak sıfıra düştüğünü görürüz (Şekil 3).
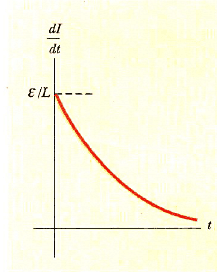
Şekil 3: Şekil 1 de görülen RI, devresi için dI/dt nin zamana göre değişimi. Akımın değişim oranı anahtar kapatıldığı zaman, t = 0 da maksimumdur. Bu oran, I kendi maksimum değerine doğru arttıkça, zamanla üstel bir şekilde azalır.
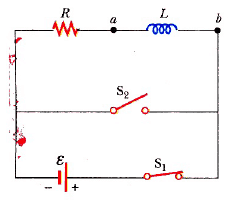
Şekil 4: İki anahtar içeren bir RL devresi. Görüldüğü gibi S1 kapanır ve S2 açılırsa, batarya devrede kalır. S2 kapatıldığı anda S1, açılırsa batarya devreden çıkmış olur.
Şimdi, Şekil 4 da görülen RL devresini göz önüne alalım. Devre, biri açıldığı zaman diğeri kapanacak şekilde iki anahtarla çalışıyor. Şimdi S1 anahtarının, akımın, ε/R denge değerine ulaşmasına yetecek kadar uzun bir süre kapatıldığını varsayalım. Bu durumda devre, tam olarak Şekil 4 ün dış halkası ile açıklanır. S1 in açıldığı anda S2 kapatılırsa, devre, tam olarak Şekil 4 ün üstteki halkası tarafından tanımlanmış olur. Alttaki halka artık devrenin davranışını etkilemez. Böylece bataryası olmayan (ε = 0) bir devreye sahip oluruz. Bu durumda, üstteki halkaya Kirchhoff ‘un devre yasasını uygularsak aşağıdaki ifadeyi elde ederiz:
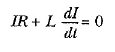
Bu diferansiyel denklemin çözümünün aşağıdaki gibi;
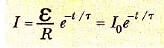
Bu durumda S, bataryanın emk’i ve I0 = ε/R, t = 0 anındaki yani S1 in açıldığı ve S2 nin kapatıldığı andaki akımdır.
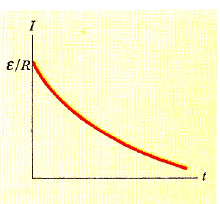
Şekil 5: Şekil 4 te görülen devrenin üstteki halkası için akımın zamana göre değişimi. x<0 da S1 kapalı ve S2 açıktır. t = 0 da kapalı S2, S1 açık ve akım, ε/R maksimum değerine sahiptir.
Devrede herhangi bir indüktör yoksa, devredeki batarya uzaklaştırıldığı anda akım, derhal sıfıra doğru azalır. Devrede indüktör varsa, bu indüktör akımdaki azalmaya karşı koyar ve akımın değerini korumaya çalışır. Akımın zamana göre grafiği (Şekil 5), zamanla sürekli olarak azaldığını göstermektedir. Ayrıca dI/dt eğiminin daima negatif ve t = 0 da maksimum değere sahip olduğuna dikkat edilmelidir. Negatif eğim,εL = -L(dI/dt) nin pozitif olduğunu vurgular; yani, Şekil 4 te a noktası b noktasından daha düşük, elektrik potansiyeldedir.
RL Devresi İle İlgili Sorular
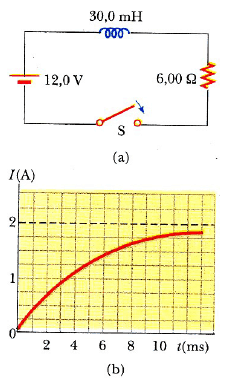
Şekil 6: (a) RL devresindeki anahtar t = 0 da kapatılmıştır. (b) (a) daki devre için akımın zamana göre grafiği.
Şekil 6 daki anahtar t = 0 anında kapatılmıştır, (a) Devrenin zaman sabitini bulunuz.
Çözüm: Zaman sabiti Eşitlik 3 ile verilir:
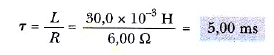
(b) t= 2,00 ms de devredeki akımı hesaplayın.
Çözüm: Zamanın fonksiyonu olarak (t ve τ ms biriminde) akım için Eşitlik 2 kullanılırsa, t = 2,00 ms de
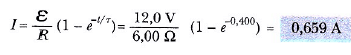
bulunur. Bu devre için Eşitlik 2 nin grafiği Şekil 6b de verilmiştir.
(c) Direncin uçları arasındaki potansiyel farkın, indüktörün uçları arasındaki potansiyel farkı ile karşılaştırın.
Çözüm: Anahtar kapatıldığı anda herhangi bir akım ve dolayısı ile direnç boyunca herhangi bir potansiyel fark yoktur. Bu anda, indüktör, sıfır – akım koşulunu korumak için, bataryanın voltajı, tümüyle indüktör boyunca, 12,0 V luk bir ters emk olarak görünür. (İndüktörün sol ucu, sağ uçtan daha yüksek bir elektriksel potansiyeldedir.) Zaman ilerledikçe, indüktörün uçları arasındaki emk azalır ve dirençten geçen akım (ve böylece uçlaeı arasındaki potansiyel fark) artar. Tüm zamanlarda, bu iki potansiyel farkının toplamı, Şekil 7 de görüldüğü gibi 12,0 V tur.
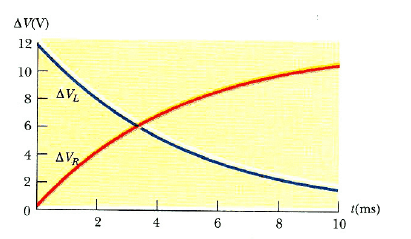
Şekil 7: Her zaman Şekil 6a daki direnç ve indüktörün uçları arasındaki potansiyel farkların toplamı 12,0 V tur (bataryanın emk’i).