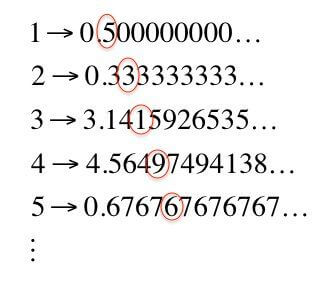Bilimin kucağında yaşlı ve bir o kadar da heybetli matematiğin, tüm bilim dalları arasında kral ya da kraliçe olduğu söylentisi kişiden kişiye değişecektir. Ama matematiğin heybetli ve ihtişamlı görünümü insanların ilgisini gün geçtikçe içine çekmiştir. Birçok çözülemeyen soru, kestirim, teorem ve paradoks derken matematiğin içindeki yapbozlar dağılmış duruma geldi. Başlıktan da anlaşılacağı üzere 0 ve 1 gibi devasa matematik sayılarının arasında sıkışmış bir hayatı konu alacağız.
İlkokul yıllarında öğretmenlerimiz ve arkadaşlarımız bizden sayı saymamızı istediğinde hemen 0,1,2,3,4,5,6… şeklinde bilgisayar gibi saymaya başlardık. Evet sizlere göre çok çok basit bir eylem olabilir fakat matematikte “sayma” gerçekten zor bir durumdur. Peki bu 0,1,2,3,4… şeklinde saydıklarımız ne? Neleri sayıyoruz? Şöyle biraz derin düşününce delirecek gibi oluyorsanız işte tam aradığımız okuyucu olma yoluna girdiğiniz demektir. Bu saydıklarımız doğal sayılar denilen esrarengiz kümelerin (sayılabilir sonsuz mu değil mi bunun okuyucu tarafından anlaşılmasını istiyoruz) birer yapı taşıdır. Daha sonra bu sayılar lise yıllarında da aynı algı biçimi ile devam eder lakin bu yanlış eğitim sisteminin bir eksikliğidir. Ah, pardon eğitim sistemini eleştirmek haddimize değil olamaz! Biz en iyisi matematik öğretim programından kaynaklanan sorundan öte gelmektedir. 0 ile 1 arasında kaç tane reel sayı var dendiğinde ise karşımıza çok farklı bir yapı çıkacaktır.
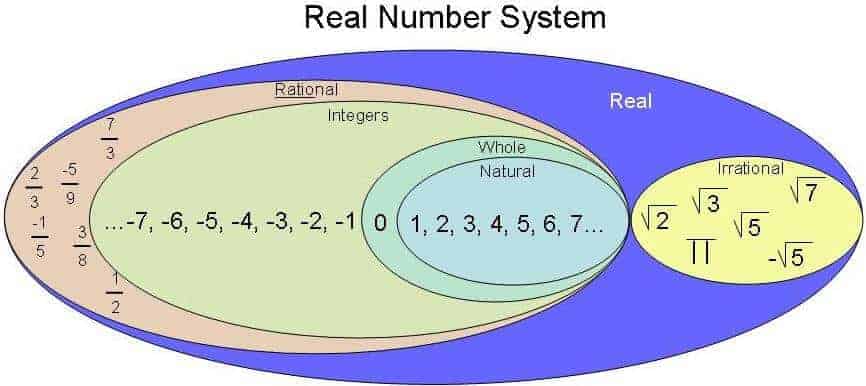
Şimdi düşünün; 0’dan yola çıkarak 1’e ulaşmaya çalışın fakat reel sayı düzlemindesiniz. Reel sayı ne demek peki? Reel sayıların aklınıza gelecek tüm sayı sistemlerini kapsayan bir uzay olarak nitelendirilebilir. Bu iki temel doğal sayı arasındaki reel sayıları en anlamlı biçimde matematik dünyasında kazandıran George Cantor olmuştur. Birçoğunuzun kümeler kuramının kurucusu olarak yakından tanıdığı bu önemli matematikçinin neler yaptığına bir bakalım. Georg Cantor’un doğal sayılar ile reel sayıların birebir eşlemesinin yapılamayacağını göstermek için geliştirdiği yöntem ile ki bu yöntem Cantor köşegen yöntemi olarak bilinir, böyle bir eşlemenin yokluğu sonsuz elemanlı kümelerin büyüklüklerinin karşılaştırılması kavramının gelişimi açısından son derece önemlidir.
0 ile 1 arasındaki reel sayılar kümesinin sayılabilir olduğunu varsayalım. Buna göre 0 ile 1 arasındaki her reel sayıya karşılık doğal sayılar kümesinde bir sayı gelmelidir. Yani iki küme birebir eşlenebilir diyoruz. Böyle bir eşlemeyi ele alalım ve 0 ile 1 arasındaki reel sayıları verilen eşleşmeye göre sıralayarak bir liste elde edelim. Bu listede sayıları küçükten büyüğe gelecek şekilde sıralamadım(bu şekilde sıralamaya gerek yoktur bu kısma takılmayın). Aşağıdaki sadece ilk 4 eşleşmeyi yazdım. Bu eşleşmenin sonsuza kadar gittiğini varsayıyoruz(önemli olan nokta burasıdır). Dolayısıyla aslında aşağıdaki birebir eşleşmede tüm doğal sayılar ve 0-1 aralığındaki tüm reel sayılar var diyoruz.
0 ile 1 arasındaki tüm reel sayıları yazdığımızı diğer bir deyişle yazabileceğimizi iddia etmiştik. Şimdi bunun aksini kanıtlayalım.
Birinci sayının ilk ondalık basamağına bakalım ve buradaki rakamdan farklı herhangi bir rakamı seçip C sayısının ilk basamağı olarak yazalım, aynı şekilde C’nin ikinci, üçüncü,… basamaklarını da oluşturalım. Mesela eğer 0 la 1 arasındaki reel sayılar aşağıdaki gibi sıralanmışsa:
s0 = 0,13567…….
s1 = 0,25678…….
s2 = 0,00212…….
s3 = 0,14291…….
C sayısının ilk basamağını 1’den farklı, 2. basamağını 5’ten farklı, 3. basamağını 2’den farklı, 4. basamağını gene 9’dan farklı birer rakam olarak seçeriz. (Varsayımımıza göre) Bu şekilde devam ederek 0 ile 1 arasındaki tüm sayıları tararız. Hatırlayın : taradığımız her reel sayıya karşılık doğal sayılar kümesinde bir sayı var(birebir eşleşme).
0 ile 1 arasında var olan tüm sayıları taradık(bu sayılara baktık) ve yukarıdaki anlattığımız yol ile bir C sayısı bulduk. C sayısının 0 ile 1 arasında olduğunu ve 0 ile 1 arasındaki tüm sayıları taradığımızı varsaymıştık. O halde taradığımız sayılardan birisi C sayısı olmalı. Halbuki C sayısı bizim taradığımız sayılardan hiçbirine eşit değil çünkü C sayısını buna göre oluşturmuştuk zaten. Gördüğünüz gibi burada bir tezatlık var. 0 ile 1 arasındaki tüm sayıları tek tek taradığımızı kabul ediyoruz.Ama elimizde 0 ile 1 aralığında öyle bir C sayısı bulduk ki taradığımız tüm sayılardan farklı. Dolayısıyla bu C sayısına karşılık gelebilecek bir doğal sayı da yok. Demek ki varsaydığımız birebir eşleme mümkün değil ve aslında reel sayılar kümesindeki eleman sayısı doğal sayılar kümesindeki eleman sayısından daha fazla. O zaman 0 ile 1 arasındaki reel sayılar kümesi sayılamaz deriz.
Referans
- Cantor – contributions to the founding of the theory of transfinite numbers – 1915
- Mathematics Stack Exchange