Merhaba sevgili okuyucu! Bugün seninle matematik dünyasının en temel kavramlarından biri olan rasyonel sayıları keşfedeceğiz. Peki, nedir bu Matematiğin Temel Taşları: rasyonel sayılar? Basitçe söylemek gerekirse, rasyonel sayılar, iki tam sayının birbirine bölümü şeklinde ifade edilebilen sayılardır. Yani a ve b tam sayı olmak üzere, a/b formunda yazılabilen her sayı bir rasyonel sayıdır. Tabii ki burada b’nin sıfır olmaması gerekiyor, çünkü biliyorsun ki matematikçiler sıfıra bölmeyi pek sevmezler!
Rasyonel Sayıların Özellikleri
Rasyonel sayılar, matematikteki diğer sayı kümelerinden farklı bazı özelliklere sahiptir. İşte bunlardan bazıları:
- Kapalılık: Rasyonel sayıları topladığında, çıkardığında, çarptığında veya böldüğünde (sıfıra bölme hariç) sonuç yine bir rasyonel sayıdır. Bu özellik, rasyonel sayılarla çalışmayı oldukça kolaylaştırır.
- Yoğunluk: Herhangi iki rasyonel sayı arasında sonsuz tane rasyonel sayı vardır. Bu, rasyonel sayıların sayı doğrusu üzerinde “sık” olduğu anlamına gelir.
- Sıralanabilirlik: Rasyonel sayıları büyüklük-küçüklük ilişkisine göre sıralayabiliriz. Bu özellik, günlük hayatta karşılaştırma yapmamızı sağlar.
- Sayılabilirlik: Tüm rasyonel sayılar sayılabilir bir küme oluşturur. Bu, matematikte önemli bir özelliktir ve rasyonel sayıları diğer sayı kümelerinden ayırır.
Rasyonel Sayıların Tarihçesi
Antik Çağlarda Rasyonel Sayılar
Rasyonel sayıların hikayesi, insanlık tarihi kadar eskidir desek yeridir. Antik Mısırlılar ve Babilliler, günlük hayatlarında ve ticaret işlemlerinde kesirli sayıları kullanıyorlardı. Örneğin, Rhind Papirüsü’nde (M.Ö. 1650 civarı) kesirli sayılarla ilgili problemler ve çözümleri bulunmaktadır.
Ortaçağ’da Rasyonel Sayılar
Ortaçağ’da, özellikle İslam dünyasında matematik büyük gelişmeler gösterdi. El-Harezmi gibi matematikçiler, cebir alanında yaptıkları çalışmalarla rasyonel sayıların anlaşılmasına ve kullanılmasına büyük katkıda bulundular. Avrupa’da ise, Leonardo Fibonacci’nin “Liber Abaci” adlı eseri, rasyonel sayıların Batı dünyasında daha iyi anlaşılmasını sağladı.
Modern Matematikte Rasyonel Sayılar
19. yüzyılda, matematikçiler rasyonel sayıları daha formal bir şekilde tanımlamaya başladılar. Richard Dedekind, rasyonel sayıları kullanarak gerçek sayıları inşa etmeyi başardı. Bu, matematikçilerin sayı sistemlerini daha derin bir şekilde anlamasını sağladı.
Rasyonel Sayıların Gösterimi
Kesir Gösterimi
Rasyonel sayıları göstermenin en yaygın yolu, kesir gösterimidir. Bir rasyonel sayıyı a/b şeklinde yazarız, burada a pay, b ise paydadır. Örneğin, 3/4, 5/2, -7/3 birer rasyonel sayıdır. Bu gösterim, rasyonel sayıların tanımıyla doğrudan ilişkilidir ve matematiksel işlemlerde sıkça kullanılır.
Ondalık Gösterim
Rasyonel sayıları ondalık gösterimle de ifade edebiliriz. Bu gösterim, günlük hayatta daha sık karşımıza çıkar. Örneğin, 3/4 = 0,75 veya 5/2 = 2,5 şeklinde yazılabilir. Bazı rasyonel sayılar sonlu ondalık açılıma sahipken (0,75 gibi), bazıları sonsuz devirli ondalık açılıma sahiptir (1/3 = 0,3333… gibi).
Yüzde Gösterimi
Yüzde gösterimi, rasyonel sayıların özel bir halidir ve günlük hayatta sıkça kullanılır. Bir sayıyı yüzde olarak ifade etmek, o sayıyı 100’e bölerek elde ettiğimiz sonucu göstermek demektir. Örneğin, %25, aslında 25/100 = 1/4 rasyonel sayısını temsil eder.
Rasyonel Sayılarda İşlemler
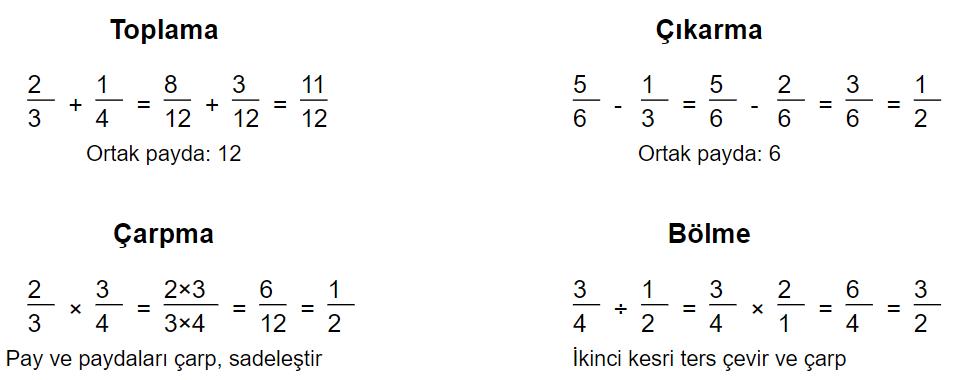
Toplama ve Çıkarma
Rasyonel sayılarla toplama ve çıkarma işlemleri, günlük hayatta sıkça karşılaştığımız durumlardan biridir. Paydaları aynı olan kesirleri toplamak veya çıkarmak oldukça kolaydır: sadece payları toplayıp veya çıkarıp, payda aynı kalır. Örneğin:
3/5 + 2/5 = (3+2)/5 = 5/5 = 1
Paydaları farklı olan kesirlerde ise önce ortak payda bulmamız gerekir:
1/2 + 1/3 = 3/6 + 2/6 = 5/6
Çarpma ve Bölme
Rasyonel sayıların çarpımı, payların çarpımının paydaların çarpımına bölümüdür:
(a/b) * (c/d) = (ac) / (bd)
Örneğin: (2/3) * (3/4) = (23) / (34) = 6/12 = 1/2
Bölme işlemi ise, böleni ters çevirip çarpma işlemine dönüştürülür:
(a/b) / (c/d) = (a/b) * (d/c) = (ad) / (bc)
Örneğin: (2/3) / (3/4) = (2/3) * (4/3) = 8/9
Üs Alma
Rasyonel sayıların üssünü almak, hem payın hem de paydanın üssünü almak anlamına gelir:
(a/b)^n = a^n / b^n
Örneğin: (2/3)^3 = 2^3 / 3^3 = 8/27
Rasyonel Sayılar Alıştırma Soruları
Çözümleri:
Rasyonel Sayıların Günlük Hayattaki Uygulamaları
Alışverişte Rasyonel Sayılar
Günlük hayatta rasyonel sayılarla en çok karşılaştığımız yerlerden biri alışveriştir. Fiyatları karşılaştırırken, indirimleri hesaplarken veya bütçe yaparken sürekli rasyonel sayıları kullanırız. Örneğin, bir ürünün %25 indirimli fiyatını hesaplarken aslında 3/4 ile çarpma işlemi yapmış oluruz.
Mutfakta Rasyonel Sayılar
Mutfakta tarif uygularken de sık sık rasyonel sayılarla karşılaşırız. Bir tarifi yarıya indirmek veya iki katına çıkarmak istediğimizde, malzeme miktarlarını rasyonel sayılarla çarparız. Örneğin, 3/4 fincan un gerektiren bir tarifi iki katına çıkarmak için 3/4 * 2 = 3/2 = 1 1/2 fincan un kullanmamız gerekir.
İnşaat ve Mühendislikte Rasyonel Sayılar
İnşaat ve mühendislik alanlarında rasyonel sayılar vazgeçilmezdir. Ölçüm yaparken, malzeme miktarlarını hesaplarken veya oranları belirlerken sürekli rasyonel sayıları kullanırız. Örneğin, beton karışımı hazırlarken çimento, kum ve su oranlarını belirlemek için rasyonel sayılar kullanılır.
Rasyonel Sayılar ve Diğer Sayı Kümeleri
Doğal Sayılar ve Rasyonel Sayılar
Doğal sayılar (1, 2, 3, …), rasyonel sayıların özel bir alt kümesidir. Her doğal sayı, paydası 1 olan bir rasyonel sayı olarak ifade edilebilir. Örneğin, 5 = 5/1 şeklinde yazılabilir. Ancak, rasyonel sayılar kümesi doğal sayılar kümesinden çok daha geniştir ve kesirli sayıları da içerir.
Tam Sayılar ve Rasyonel Sayılar
Tam sayılar kümesi (…, -2, -1, 0, 1, 2, …), doğal sayılar kümesini, sıfırı ve negatif tam sayıları içerir. Tüm tam sayılar da rasyonel sayılar kümesinin bir alt kümesidir. Her tam sayı, paydası 1 olan bir rasyonel sayı olarak yazılabilir.
İrrasyonel Sayılar ve Rasyonel Sayılar
İrrasyonel sayılar, rasyonel sayılar gibi iki tam sayının oranı şeklinde ifade edilemeyen sayılardır. √2, π, e gibi sayılar irrasyonel sayılara örnektir. Rasyonel ve irrasyonel sayıların birleşimi gerçek sayılar kümesini oluşturur. İrrasyonel sayılar, rasyonel sayılardan farklı olarak, sonsuz ve tekrarsız ondalık açılıma sahiptir.
Rasyonel Sayıların Öğretimi
İlkokul Düzeyinde Rasyonel Sayılar
İlkokul düzeyinde rasyonel sayıların öğretimi genellikle kesirler üzerinden yapılır. Öğrenciler önce bütün-parça ilişkisini anlamaya çalışır. Örneğin, bir pizzanın dörtte biri (1/4) gibi somut örnekler üzerinden kesir kavramı anlatılır. Daha sonra basit kesir işlemleri ve kesirlerin karşılaştırılması gibi konulara geçilir.
Ortaokul Düzeyinde Rasyonel Sayılar
Ortaokul seviyesinde, rasyonel sayılar kavramı daha formal bir şekilde ele alınır. Öğrenciler, rasyonel sayıların tanımını öğrenir ve farklı gösterim biçimlerini (kesir, ondalık, yüzde) kullanmaya başlar. Bu düzeyde, rasyonel sayılarla dört işlem, negatif rasyonel sayılar ve rasyonel sayıların sayı doğrusunda gösterimi gibi konular işlenir.
Lise Düzeyinde Rasyonel Sayılar
Lise düzeyinde, rasyonel sayılar daha ileri matematiksel kavramlarla ilişkilendirilir. Öğrenciler, rasyonel sayıların özelliklerini daha derinlemesine inceler, rasyonel ve irrasyonel sayılar arasındaki farkı anlar ve rasyonel sayıların matematikteki rolünü daha geniş bir perspektiften değerlendirir. Ayrıca, limit kavramı ve rasyonel fonksiyonlar gibi konularda rasyonel sayılar önemli bir rol oynar.
Rasyonel Sayılarla İlgili Yanılgılar ve Zorlu Kavramlar
Sıfırla Bölme Yanılgısı
Rasyonel sayılarla ilgili en yaygın yanılgılardan biri, sıfıra bölme konusudur. Birçok öğrenci, bir sayının sıfıra bölünebileceğini düşünür. Ancak, matematiksel olarak bir sayıyı sıfıra bölmek tanımsızdır. Bu kavramı anlatmak için günlük hayattan örnekler kullanmak faydalı olabilir. Örneğin, 10 elmayı 0 kişiye paylaştırmaya çalışmanın imkansız olduğunu hayal etmelerini isteyebiliriz.
Sonsuz Ondalık Açılım Kavramı
Bazı rasyonel sayıların sonsuz ondalık açılıma sahip olması, öğrenciler için zor bir kavram olabilir. Örneğin, 1/3 = 0,333333… şeklinde sonsuza kadar gider. Bu durumu anlatmak için, öğrencilere bir çemberin çevresini çapına böldüğümüzde elde ettiğimiz π sayısının da sonsuz ondalık açılıma sahip olduğunu, ancak π’nin irrasyonel bir sayı olduğunu hatırlatabiliriz.
Yoğunluk Özelliği
Rasyonel sayıların yoğunluk özelliği, yani herhangi iki rasyonel sayı arasında sonsuz sayıda rasyonel sayı olması, kavramsal olarak zorlayıcı olabilir. Bu kavramı anlatmak için, öğrencilere iki rasyonel sayı arasındaki aritmetik ortalamayı bulma alıştırmaları yaptırabiliriz. Örneğin, 1/2 ile 3/4 arasındaki sayıyı bulma: (1/2 + 3/4) / 2 = 5/8.
Rasyonel Sayıların Bilgisayar Bilimindeki Rolü
Bilgisayarlarda Rasyonel Sayı Temsili
Bilgisayar biliminde, rasyonel sayıların temsili önemli bir konudur. Bilgisayarlar, sınırlı bellek kapasitesine sahip olduklarından, rasyonel sayıları tam olarak temsil etmek her zaman mümkün olmayabilir. Bu nedenle, birçok programlama dili ve bilgisayar sistemi, rasyonel sayıları yaklaşık değerlerle temsil eder.
Örneğin, ondalık gösterimde 1/3 sayısını tam olarak temsil etmek mümkün değildir (0,333333…). Bilgisayarlar genellikle bu sayıyı belirli bir hassasiyete kadar yuvarlar (örneğin, 0,33333333). Bu durum, özellikle hassas hesaplamalar gerektiren bilimsel ve finansal uygulamalarda dikkat edilmesi gereken bir konudur.
Hesaplama Hassasiyeti ve Rasyonel Sayılar
Rasyonel sayıların bilgisayarlarda yaklaşık değerlerle temsil edilmesi, bazı hesaplamalarda hassasiyet sorunlarına yol açabilir. Özellikle, çok küçük veya çok büyük sayılarla yapılan işlemlerde veya çok sayıda işlemin art arda yapıldığı durumlarda bu sorunlar ortaya çıkabilir.
Bu sorunu aşmak için, bazı programlama dilleri ve matematiksel yazılımlar, rasyonel sayıları kesir olarak (pay ve payda şeklinde) temsil eden özel veri tipleri sunar. Bu sayede, rasyonel sayılarla yapılan işlemlerde hassasiyet kaybı minimize edilir.
Örneğin, Python programlama dilinde fractions modülü, rasyonel sayıları hassas bir şekilde temsil etmek ve işlemek için kullanılabilir:
from fractions import Fraction a = Fraction(1, 3) b = Fraction(1, 6) c = a + b print(c) # 1/2 print(float(c)) # 0.5
Bu örnekte, 1/3 ve 1/6 rasyonel sayıları hassas bir şekilde temsil edilmiş ve toplanmıştır. Sonuç, 1/2 şeklinde kesin olarak elde edilmiştir.
Sonuç
Rasyonel sayılar, matematiğin temel yapı taşlarından biridir ve günlük hayatımızdan bilimsel çalışmalara kadar pek çok alanda karşımıza çıkar. Bu sayıların anlaşılması, matematiksel düşünme becerilerimizi geliştirirken, problem çözme yeteneklerimizi de artırır.
Rasyonel sayıların tarihsel gelişimi, insanlığın sayı kavramını nasıl derinleştirdiğini ve matematiği nasıl ilerlettiğini gösterir. Günümüzde ise rasyonel sayılar, ilkokuldan üniversiteye kadar eğitimin her aşamasında önemli bir yer tutar.
Bilgisayar biliminde rasyonel sayıların temsili ve işlenmesi, hassas hesaplamalar gerektiren alanlarda kritik öneme sahiptir. Bu nedenle, rasyonel sayıların doğasını ve özelliklerini iyi anlamak, hem matematikçiler hem de bilgisayar bilimciler için vazgeçilmezdir.
Sonuç olarak, rasyonel sayılar matematiğin ve bilimin gelişiminde önemli bir rol oynamaya devam edecektir. Bu sayıları anlamak ve etkili bir şekilde kullanmak, problem çözme becerilerimizi geliştirirken, dünyayı daha iyi anlamamıza da yardımcı olacaktır.
Sıkça Sorulan Sorular
- Rasyonel sayılar ve irrasyonel sayılar arasındaki fark nedir? Rasyonel sayılar, iki tam sayının birbirine oranı şeklinde ifade edilebilen sayılardır (örneğin, 3/4, 5/2). İrrasyonel sayılar ise bu şekilde ifade edilemeyen sayılardır (örneğin, π, √2). İrrasyonel sayıların ondalık gösterimi sonsuza kadar devam eder ve tekrar etmez.
- Neden 0/0 belirsizdir, ama 7/0 tanımsızdır? 0/0 belirsizdir çünkü bu ifade birçok farklı değer alabilir. Örneğin, x/x = 1 eşitliğinde x yerine 0 koyarsak 0/0 = 1 elde ederiz. Ancak y*0 = 0 eşitliğinde y’nin herhangi bir değer alabileceğini düşünürsek, 0/0 herhangi bir sayı olabilir. 7/0 ise tanımsızdır çünkü hiçbir sayı 0 ile çarpıldığında 7 vermez.
- Rasyonel sayıların yoğunluk özelliği ne anlama gelir? Rasyonel sayıların yoğunluk özelliği, herhangi iki rasyonel sayı arasında sonsuz sayıda rasyonel sayı olduğu anlamına gelir. Bu, rasyonel sayıların sayı doğrusu üzerinde “sık” olduğunu gösterir. Örneğin, 1 ve 2 arasında 3/2, 4/3, 5/4 gibi sonsuz sayıda rasyonel sayı vardır.
- Rasyonel sayıların günlük hayatta kullanımına başka örnekler verebilir misiniz? Rasyonel sayılar günlük hayatımızda sıkça karşımıza çıkar. Örneğin, yemek tariflerinde malzeme ölçüleri (1/2 bardak un), zaman ifadelerinde (3/4 saat), spor istatistiklerinde (basketbolda serbest atış yüzdesi), faiz oranlarında ve oran-orantı problemlerinde (2:3 oranında karıştırılan bir içecek) rasyonel sayıları kullanırız.