Pi sayısı ile ilgili karşımıza çıkan bilenleriniz olmasına rağmen bilmeyenlerimizin de çoğunluk olduğu bir yaklaşımdan söz edeceğiz. Şimdi pi sayısının uzayıp giden ondalık kısmını unutun ve pi sayısının 2 olduğunu kanıtlayalım. Bu kanıtın saçmalık olduğunu sakın aklınızın ucunda geçirmeyin çünkü bu sizin beyninizi yıkayacak bir ispat ya da yanlış…
Şunu biliyoruz ki bir çemberin (hangi çember olursa olsun) çevresinin çapına bölümü pi sayısını verecektir. Şimdi hemen bir görsel ile söylediğimizi aktaralım.
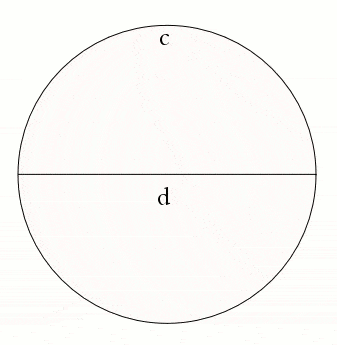
Şimdi çevresi 2 olan bir çember düşünün ve bunun yarısı olan çemberin de doğal olarak çevresinin 1 olacağını hayal edin. Şimdi, dairenin çapını “d”’yi yarıya bölelim ve her iki yarımın her birinde yeni, daha küçük bir yarı daire çizelim. Yani git gide yarım kesitleri alınarak yeni şekiller elde edeceğiz.
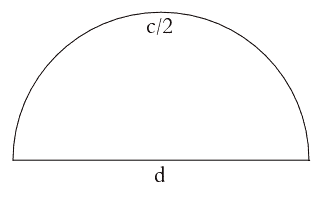
Diğer bir söyleşiyle çemberin çapı ve çevresi yarı yarıya azalacaktır. Bunu 4 adım daha devam ettirelim ve orijinal çapın 1/4 oranında yarı daireler elde edin. Bu durumda çemberlerin iç içe olacağını unutmayalım. Bunu bu şekilde devam ettirdiğinizde n. adımda 2’nin n. kuvvetleri olacak biçimde yarım çemberleriniz olacak ve bunların her birinin uzunluğu 1/2^n şeklinde devam edip gidecektir.
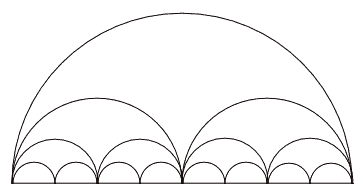
Baktığımız zaman bu durumda limit kavramının ortaya girdiğini görüyoruz. Her aşamada daha da küçük hale gelen bu yarım çemberler belirli bir müddetten sonra en büyük yarım çemberin çapını oluşturan bir çizgi haline gelecektir. Yani limitini eğer doğru hesaplarsak ilk görseldeki “d” ile gösterilen çapı elde edeceğiz. Yani d, n’nin sonsuzluk eğilimine girdiği basamak sayısı olarak bu toplamın sınırlanmış biçimidir. Yani şu şekilde yazsak doğru olmaz mı?
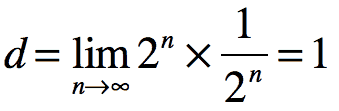
Evet… Fakat, büyük çemberin çevresinin çevresinin 2 olduğunu biliyoruz. π sayısının c/d olduğunu bildiğimize göre π=2/1=2 olacaktır.
Nerede yanlış yaptık? Matematik konuşalım hadi…
“Plus Mathematics / Cambridge University” dergisinin izni dahilinde araştırılmıştır.

