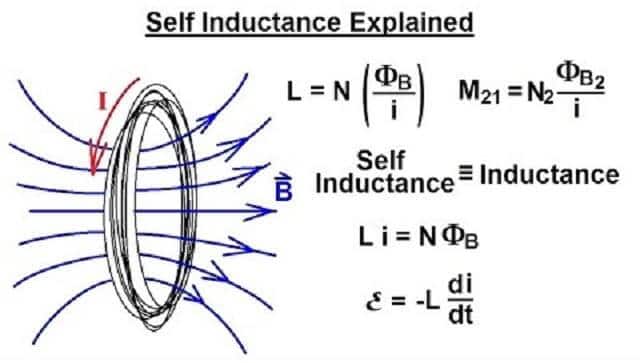
“Öz indüksiyon akımı” terimi, bir elektrik devresinde oluşan bir fenomeni tanımlar. İndüksiyon, bir akım taşıyan iletkenin yakınında bir manyetik alanın değişmesi sonucunda iletkenin içinde bir elektrik akımı oluşturmasıdır. Öz indüksiyon ise, bu manyetik alan değişikliğinin aynı iletken içinde olması durumunu ifade eder.
Bir devrede, akımın yönü aniden değişirse veya devredeki manyetik alanın şiddeti aniden artarsa, bu durumda devre içinde kendine özgü bir indüksiyon akımı oluşur. Bu indüksiyon akımı, değişen manyetik alan tarafından devredeki iletkenlerin içinde oluşturulur.
Öz indüksiyon akımı, elektromanyetizma ve devre teorisi gibi fizik dallarında önemli bir konudur ve manyetik alanın elektrik akımına etkisi üzerine çalışır. Bu akım, Faraday’ın elektromanyetik indüksiyon yasasına dayanır ve elektromanyetik alan ve elektriksel akımdaki değişiklikler arasındaki ilişkiyi açıklar.
Bataryalar ve diğer kaynakların oluşturduğu emk’ler ve akımlar ile, değişen manyetik alanların indükledikleri arasındaki farkı ayırt etmemiz gerekiyor. Kaynak sıfatını (emk kaynağı ve akım kaynağı ifadelerinde kullandığımız üzere), bir fiziksel kaynağa eşlik eden parametreleri tanımlamak için, indüklenmiş sıfatını ise, değişen bir manyetik alanın sebep olduğu emk’ler ve akımlar için kullanıyoruz.
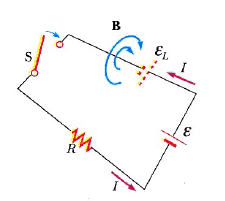
Şekil 1 de görüldüğü gibi, anahtar, direnç ve emk kaynağından oluşan yalıtılmış bir devreyi düşünelim. Anahtar kapatıldığında akım hemen sıfırdan maksimum değeri, olan ε/R ye yükselmez. Faraday’ın elektromanyetik indüksiyon yasası bu olayı açıklamak için aşağıdaki gibi kullanılabilir: Akım zamanla arttıkça, bu akımdan ileri gelen ve halkadan geçen akı da artar. Artmakta olan bu akı, devrede bir emk indükler. Bu indüklenmiş emk’in yönü, halkada indüklenmiş bir akıma sebep olacak türdedir (eğer halkada önceden bir akım akmıyorsa); oluşan bu akım da kaynak manyetik alandaki değişiklikliğe karşı koyacak yönde bir manyetik alan kurar. Böylece, indüklenmiş emk’in yönü, kaynağın emk’ın yönünün tersidir. Bu durum, kaynak akımının, son denge değerine doğru ani bir artış yerine kademeli bir artış yapmasına neden olur. Bu olay, devreden geçen değişen akının ve ortaya çıkan indüklenmiş emk’in, devrenin kendisinden kaynaklandığı için, öz-indüksiyon olarak adlandırılır. Bu durumda ortaya çıkan εL emk’i, öz indüksiyon emk’i olarak bilinir. Buna, çoğu zaman zıt emk da denir.
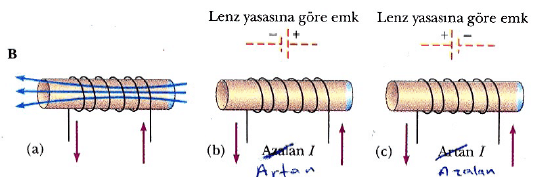
Şekil 2(a) Bobinde ki akım, sola doğru yönelmiş bir manyetik alan meydana getirir, (b) Bu akım artarsa, artan manyetik akı, kesikli batarya ile gösterilen kutuplan olan bir emk indükler. (c) Akım azalırsa, bu indüklenmiş emk ters işaretli olur.
Öz indüksiyona ikinci bir örnek olarak, silindir biçiminde bir demirin etrafına sarılmış bir bobini gösteren Şekil 2 yi göz önüne alın. (Uygulamada böyle bir aygıt, bir kaç yüz sarmalıdır.) Bobindeki kaynak akımının zamanla arttığını ya da azaldığını varsayın. Kaynak akımı şekilde gösterilen yönde olduğu zaman, Şekil 2a da görüldüğü gibi, bobin içinde sağdan sola doğru yönelen bir manyetik akı da değişir ve bobinde bir emk indüklenir. Lenz yasasına göre bu indüklenmiş emk’in kutupları Şekil 2b’de görüldüğü gibi, kaynak akımından ileri gelen manyetik alanın değişimine karşı koyarak yönde olmalıdır; kaynak akımı azalıyorsa, indüklenmiş emk’in kutupları Şekil 2c de görüldüğü gibidir.
Öz indüksiyonun nicel bir anlatımını vermek için, indüksiyon emk’in, manyetik akının zamana göre değişim hızının negatifi olduğunu Faraday yasasından hatırlamalıyız. Manyetik akı, kaynak akıntından ileri gelen manyetik alanla orantılı ve dolayısıyla devredeki kaynak akımla da orantılıdır. Bu nedenle, εL öz indüksiyon emk’i daima akımın zamana göre değişim hızıyla orantılıdır. Belli geometrideki (toroid şeklinde bobin veya ideal solenoid) sıkıca sarılmış N sarımlı bir bobin için,
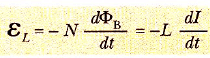
ifadesi bulunur. Buradaki L, devrenin geometrik özelliklerine ve diğer fiziksel karakteristiklere bağlı olan ve devrenin indüktansı olarak adlandırılan bir orantı sabitidir. Bu ifadeden, N sarım içeren bir bobinin indüktansının
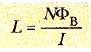
denklemiyle verildiğini görürüz. Burada her sarımdan aynı akının geçtiği varsayılmıştır. Daha sonra, bu denklemi bazı özel devre geometrilerinin indüktansını hesaplamak için kullanacağız.
Eşitlik 1 den, indüktansı
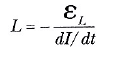
oranı şeklinde de yazabiliriz. Direncin, akıma karşı gelmenin bir ölçüsü olması (R = ΔV/I) gibi, indüktansı da akımdaki değişime karşı koymanın bir ölçüsüdür.
İndüktansın SI birimi henri (H) olup, Eşitlik 3 e göre, 1 volt-s /ampere eşit olduğu görülmektedir:
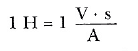
Bir aygıtın indüktansının kendi geometrisine bağlı olması, bir kondansatörün sığasının, plakaların geometrisine bağlı olmasına benzemektedir. Karmaşık geometriler için indüktans hesaplamalarını gerçekleştirmek oldukça güçtür.