Newton Kanunlarının Bazı Uygulamaları

Bu yazımızda, dengede (a = 0) veya sabit bir dış kuvvet etkisi altında ivmeli doğ­rusal hareket yapan bir cisim için, Newton kanunlarının bazı uygulamaları sunulacaktır. Modelimize göre burada cismin, bir paçacık gibi davrandığını varsayacağız: dolayısıyla dönme hareketleriyle ilgilenmemiz gerekmez. Bu kesimde ayrıca, sürtünmenin etkilerini ihmal edeceğiz. Bu, yüzeyin sürtünmesiz olduğu ifadesi ile eşdeğerdir. Böyle problemlerde, cisimlerin bağlı oldukları iplerin kütlelerini de genellikle ihmal edeceğiz. Bu yaklaşımlara göre, ip bo­yunca herhangi bir noktaya uygulanan kuvvet ipin her noktası için aynı ola­caktır. Problemlerde hafif, hafif ağırlıklı ve ihmal edilebilir kütle terimleri aynı an­lamlıdır ve problemlerde kütle ihmal edilmelidir.

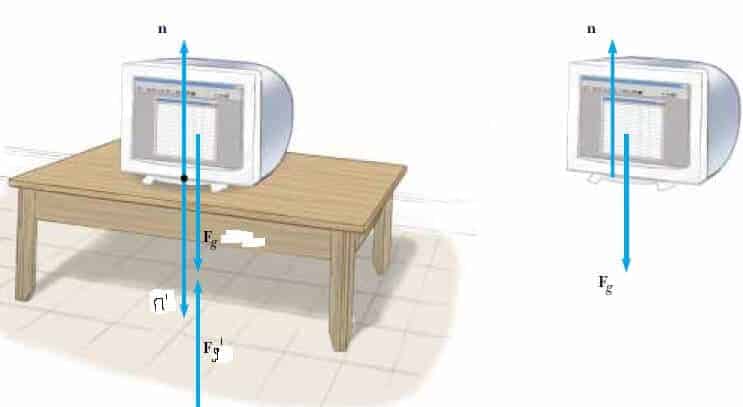
Newton kanunları bir cisme uygularken, sadece cisim üzerine etki eden dış kuvvetlerle ilgileneceğiz. Örneğin Şekil 1 de TV ye etki eden dış kuvvetler sa­dece n ve F_g dir. Bu kuvvetlere tepki olarak doğan n’ ve F_g‘ kuvvetleri, masaya ve yere etki ederler. Bundan dolayı n’ ve F_g Newton’un ikinci yasasında, TV ye etkiyen kuvvetler arasında bulunmazlar.

Bir cisim bir sicim ile çekildiği zaman, sicim, cisime bir T kuvveti uygular ve bu kuvvetin büyüklüğüne gerilme denir. Gerilme, skaler bir niceliktir, çün­kü bir vektörel niceliğin büyüklüğüdür.

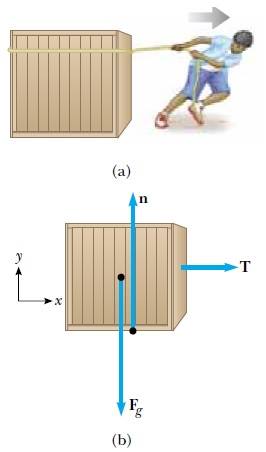
Şekil 2a da görüldüğü gibi düzgün, yatay bir zemin üzerinde sağ tarafa doğru çekilen bir bloğu gözönüne alalım. Bloğun ivmesinin ve zeminin bloğa uyguladığı kuvvetin sorulduğunu varsayalım. Önce bloğa uygulanan yatay kuvvete dikkat edelim. Kuvvet, bloğa ip boyunca uygulanır. İpin bloğa uyguladığı kuvvet T ile gösterilir. T nin büyüklüğü ipteki gerilmeye eşittir. Şekil 2a da bloğun etrafına çizilen noktalı çember onun çevresinden izole edildiğini be­lirtmektedir. Sadece bloğun hareketi ile ilgilendiğimizden, bloğa etki eden bütün kuvvetlerin tanımlanabilmesi gerekir. Bu kuvvetler Şekil 2b de göste­rilmiştir. T kuvveti ile beraber blok üzerine F_g ağırlığı ve n normal kuvveti de etki eder. Bloğa etki eden kuvvetlerin gösterilmesine serbest-cisim diyagramı (çizeneği) denir. Newton kanunları uygulanmasında böyle bir diyagramın çi­zilmesi önemli bir adımdır. Cisme etki etmeyen, ipin ele, bloğun zemine uy­guladığı tepki kuvvetleri serbest cisim diyagramında görülmez. Sadece cisme etki eden kuvvetler, o cismin serbest cisim diyagramında görülür.

Şimdi Newton’un ikinci yasasının bileşenlere ayrılmış şeklini Şekil 2 de­ki sisteme uygulayabiliriz. x yönünde sadece T kuvveti etki eder. Yatay doğrul­tudaki harekete ∑F_y = ma_x ifadesini uygulayarak a_x bulunur:

∑F_x = T = ma_x    veya  a_x =T/m

Bu durumda y yönünde ivme mevcut değildir. ∑F_y = ma_y eşitliğinde a_y = 0 olduğundan

n + (-F_g) = 0     veya     n = F_g

 bulunur. Yani, normal kuvvet, ağırlığa eşit ve onunla zıt yönlüdür.

T sabit bir kuvvet ise a_x = T/m ivmesi de sabittir. Böylece kinematik eşitlikler; Δx yerdeğiştirmesi ve v hızını, zamanın fonksiyonu ola­rak bulmak için kullanılabilir. a_x = T/m sabit olduğundan, t = 0 anında v_x = v_xi  olmak şartıyla yerdeğiştirme ve hız ifadeleri aşağıdaki gibi elde edilir:

v_xs = v_xi  + (T/m)t

Δx= v_xit + 1/2(T/m)t²

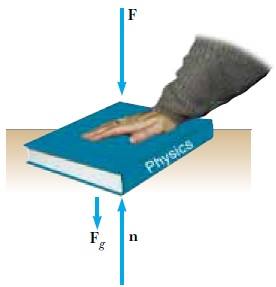
Az önce gösterilen örnekte, n normal kuvveti, cismin F_g çekim kuvvetine büyüklükçe eşit ve onunla zıt yönlü idi. Bu her zaman böyle olmaz. Örneğin, Şekil 3 de görüldüğü gibi bir kitabı üsten bir F kuvveti ile bastırdığınızı varsayalım. Bu halde  ∑F_y = 0 dır. Buradan, n – F_g –  F= 0 veya n = F_g + F olur. İçin­de n ≠ F_g olan diğer örnekler ileride görülecektir.

Şekil 4a da görüldüğü gibi, ağırlıksız kabul edilen bir zincirle tavana asılan bir lambayı ele alalım. Lamba için serbest-cisim diyagramı Şekil 4b de gösterilmiştir. Burada lambaya etkiyen kuvvetler aşağı yönlü F_g kuvveti ile zincirin yukarı yönde uyguladığı T kuvvetidir. Bu durumda T bir gerilme kuv­vetidir. (Zincir kesilirse T = 0 olur ve cisim serbest düşme hareketi yapar.)

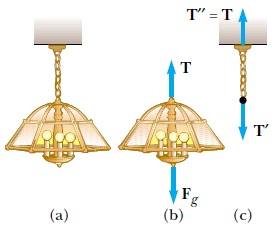
Lambaya, a = 0 olduğuna dikkat ederek Newton’un birinci yasasını uygu­larsak, x doğrultusunda bir kuvvet bulunmadığından, ∑F_y = 0 eşitliği yararlı bir bilgi vermez. ∑F_y = 0 şartı ise,

 ∑F_y = T – F_g  = 0       veya       T = F_g

 olacağını söyler. Burada T ve F_g nin etki-tepki kuvvetleri olmadığına dikkat edil­melidir. T kuvvetine tepki olarak doğan kuvvet, Şekil 4c de görüldüğü gibi T’ dür. T’ aşağı doğru etki eder ve zincir vasıtasıyla tavana aktarılır. T’ aşağı doğrudur ve büyüklükçe ağırlığa eşittir. Şekil 4c de görüldüğü gibi tavan, zincire bir T” kuvveti uygular, bunun büyüklüğü, T’ nün büyüklüğüne eşit ve yönce ters olur.

Bu yazımızda sizlere Newton Kanunlarının Bazı Uygulamalarını anlattık. Diğer yazılarımızda görüşmek üzere.