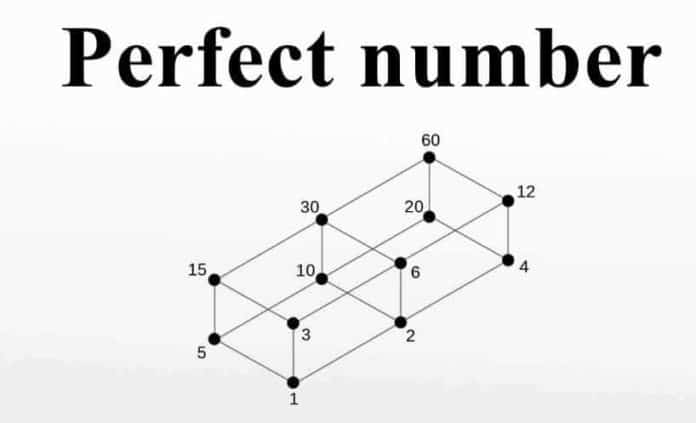
Matematikte rastgele diye bir kavram yoktur. Doğayı oluşturan hiçbir şeyin tesadüf olmadığı gibi matematiksel yapılarda bulacağımız ve tesadüfi olmayan ve çözülmeyi bekleyen Mükemmel sayı kavramıdır. Nedir bu mükemmel sayı? Mükemmel sayı kendisi haricindeki tüm çarpanlarının toplamı kendisini veren sayıdır. Diğer bir ifadeyle, mükemmel sayı, bütün pozitif tam bölenlerinin toplamının yarısına eşit olan sayıdır.
Örneğin 6 bir mükemmel sayıdır çünkü kendisi haricindeki çarpanları yani 1, 2 ve 3 toplanınca kendisini verir: 1 + 2 + 3 = 6. Veya bütün pozitif tam bölenlerinin toplamının yarısı kendisini verir: 1 + 2 + 3 + 6 = 12 ve 12 / 2 = 6
Euclid ilk dört mükemmel sayı üstünde yaptığı araştırmalarda p asal sayı olmak üzere şöyle bir formül ile tanımlanabildiklerini keşfetmiştir: 2p−1(2p−1). Buna göre ilk dört mükemmel sayı şu şekilde hesaplanabilir:
p = 2: 21(22−1) = 6
p = 3: 22(23−1) = 28
p = 5: 24(25−1) = 496
p = 7: 26(27−1) = 8128
2013 yılına kadar bulunan mükemmel sayılar:
| Sıra | p sabiti | Mükemmel Sayı | Basamak | Yıl | Sayıyı Bulan |
|---|---|---|---|---|---|
| 1 | 2 | 6 | 1 | Eski Yunan | |
| 2 | 3 | 28 | 2 | Eski Yunan | |
| 3 | 5 | 496 | 3 | Eski Yunan | |
| 4 | 7 | 8128 | 4 | Eski Yunan | |
| 5 | 13 | 33550336 | 8 | 1456 | İlk görülme bir ortaçağ el yazması: Codex Lat. Monac |
| 6 | 17 | 8589869056 | 10 | 1588 | Cataldi |
| 7 | 19 | 137438691328 | 12 | 1588 | Cataldi |
| 8 | 31 | 2305843008139952128 | 19 | 1772 | Euler |
| 9 | 61 | 265845599…953842176 | 37 | 1883 | Pervushin |
| 10 | 89 | 191561942…548169216 | 54 | 1911 | Powers |
| 11 | 107 | 131640364…783728128 | 65 | 1914 | Powers |
| 12 | 127 | 144740111…199152128 | 77 | 1876 | Lucas |
| 13 | 521 | 235627234…555646976 | 314 | 1952 | Robinson |
| 14 | 607 | 141053783…537328128 | 366 | 1952 | Robinson |
| 15 | 1,279 | 541625262…984291328 | 770 | 1952 | Robinson |
| 16 | 2,203 | 108925835…453782528 | 1,327 | 1952 | Robinson |
| 17 | 2,281 | 994970543…139915776 | 1,373 | 1952 | Robinson |
| 18 | 3,217 | 335708321…628525056 | 1,937 | 1957 | Riesel |
| 19 | 4,253 | 182017490…133377536 | 2,561 | 1961 | Hurwitz |
| 20 | 4,423 | 407672717…912534528 | 2,663 | 1961 | Hurwitz |
| 21 | 9,689 | 114347317…429577216 | 5,834 | 1963 | Gillies |
| 22 | 9,941 | 598885496…073496576 | 5,985 | 1963 | Gillies |
| 23 | 11,213 | 395961321…691086336 | 6,751 | 1963 | Gillies |
| 24 | 19,937 | 931144559…271942656 | 12,003 | 1971 | Tuckerman |
| 25 | 21,701 | 100656497…141605376 | 13,066 | 1978 | Noll & Nickel |
| 26 | 23,209 | 811537765…941666816 | 13,973 | 1979 | Noll |
| 27 | 44,497 | 365093519…031827456 | 26,790 | 1979 | Nelson & Slowinski |
| 28 | 86,243 | 144145836…360406528 | 51,924 | 1982 | Slowinski |
| 29 | 110,503 | 136204582…603862528 | 66,530 | 1988 | Colquitt & Welsh |
| 30 | 132,049 | 131451295…774550016 | 79,502 | 1983 | Slowinski |
| 31 | 216,091 | 278327459…840880128 | 130,100 | 1985 | Slowinski |
| 32 | 756,839 | 151616570…565731328 | 455,663 | 1992 | Slowinski & Gage |
| 33 | 859,433 | 838488226…416167936 | 517,430 | 1994 | Slowinski & Gage |
| 34 | 1,257,787 | 849732889…118704128 | 757,263 | 1996 | Slowinski & Gage |
| 35 | 1,398,269 | 331882354…723375616 | 841,842 | 1996 | Armengaud, Woltman, et al. |
| 36 | 2,976,221 | 194276425…174462976 | 1,791,864 | 1997 | Spence, Woltman, et al. |
37 |
3,021,377 |
811686848…022457856 |
1,819,050 |
1998 |
Clarkson, Woltman, Kurowski, et al. |
| 38 | 6,972,593 | 955176030…123572736 | 4,197,919 | 1999 | Hajratwala, Woltman, Kurowski, et al. |
| 39 | 13,466,917 | 427764159…863021056 | 8,107,892 | 2001 | Cameron, Woltman, Kurowski, et al. |
| 40 | 20,996,011 | 793508909…206896128 | 12,640,858 | 2003 | Shafer, Woltman, Kurowski, et al. |
| 41 | 24,036,583 | 448233026…572950528 | 14,471,465 | 2004 | Findley, Woltman, Kurowski, et al. |
| 42 | 25,964,951 | 746209841…791088128 | 15,632,458 | 2005 | Nowak, Woltman, Kurowski, et al. |
| 43 | 30,402,457 | 497437765…164704256 | 18,304,103 | 2005 | Cooper, Boone, Woltman, Kurowski, et al. |
| 44 | 32,582,657 | 775946855…577120256 | 19,616,714 | 2006 | Cooper, Boone, Woltman, Kurowski, et al. |
| 45 | 37,156,667 | 204534225…074480128 | 22,370,543 | 2008 | Elvenich, Woltman, Kurowski, et al. |
| 46 | 42,643,801 | 144285057…377253376 | 25,674,127 | 2009 | Strindmo, Woltman, Kurowski, et al. |
| 47 | 43,112,609 | 500767156…145378816 | 25,956,377 | 2008 | Smith, Woltman, Kurowski, et al. |
| 48 | 57,885,161 | 169296395…270130176 | 34,850,340 | 2013 | Cooper, Woltman, Kurowski, et al. |
Şimdilik bu sayılar arasında başka mükemmel sayı olup olmadığı bilinmiyor.
Şimdi gelelim asıl probleme:
Dikkat ederseniz bilinen bütün mükemmel sayılar çift sayılar. Şimdiye kadar hiç tek mükemmel sayı bulunamamış. Yıllardır bilim adamları tek mükemmel sayı bulmaya veya tek mükemmel sayı olamayacağını ıspatlamaya çalışıyorlar.
Bu yazıda belirtilen tablodaki veriler Wikipedia’dan alınmıştır. Umarım başka bir mükemmel sayıyı sizler bulursunuz. Matematikle kalın