Moleküler Hız Dağılımı

1860 yılında James Clerk Maxwell (1831-1879) moleküler hız dağılımını oldukça doğru tahmin eden bir bağıntı türetmiştir. Maxwell ve diğer araştırmacılar tarafından yapılan çalışmalar çelişkiler içindeydi. Çünkü o yıllarda molekülleri doğrudan algılayabilecek yeterli deneyler yapılamıyordu. Fakat 60 yıl sonra yapılan deneyler Maxwell’in öngörülerini doğruluyordu.

Bir kap içindeki gaz molekülleri aynı hız dağılımına sahip olsun. Örneğin hızları 400-410 m/s aralığında olan kaç tane gaz molekülü olduğunu tayin etmek istediğimizi varsayalım. Sezgisel olarak, hız dağılımının sıcaklığa bağlı olmasını, hatta V_kök yakınında dağılımın bir tepe noktasının bulunmasını bekleriz. Yani hızları V_kök değerinden çok az veya çok fazla olan sadece birkaç molekül beklenir. Çünkü böyle aşırı büyük ve küçük hızlar ancak, olası görünmeyen zincirleme çarpışmalardan ortaya çıkar.

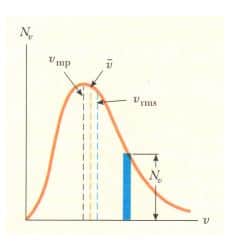
Isıl dengeye ulaşan gaz moleküllerinde gözlenen hız dağılımı Şekil 1’de gösterilmiştir. Maxwell Boltzmann dağılım fonksiyonu denilen N_v niceliği aşağıdaki gibi tanımlanır:

Eğer moleküllerin toplam sayısı N’ise, hızları v ile v + dv arasında olan moleküllerin sayısı dN = dv/N’dir. Bu sayı aynı zamanda Şekil 1’deki gölgeli dikdörtgenin alanına eşittir. Üstelik hızı v ile v + dv arasında olan moleküllerin kesri N_v dv/N’dir. Bu oran aynı zamanda, bir molekülün hızının v ile v+ dv arasındaki olasılığına eşittir.

N sayıdaki gaz moleküllerinin hız dağılımını ifade eden temel ifade aşağıdaki gibidir.

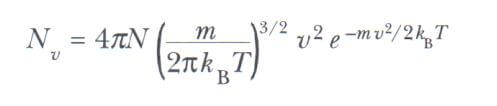
Burada m bir gaz molekülünün kütlesi, k_B Boltzmann sabiti ve T mutlak sıcaklıktır. E= 1/2(m.v²) olmak üzere Boltzmann çarpanı olan е^-E/k_BT nin görüşünü inceleyiniz.

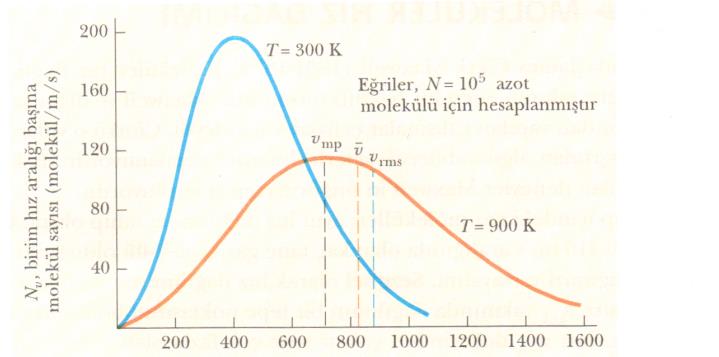
Şekil 1’den de görüleceği gibi, v ortalama hızı, V_kök (V_rms ) hızından biraz küçüktür. V_mp en muhtemel hızdır. Bu hızda, dağılım eğrisinin tepe değerine ulaşılır. Üstteki eşitlik kullanılarak aşağıdaki eşitlikler bulunur:

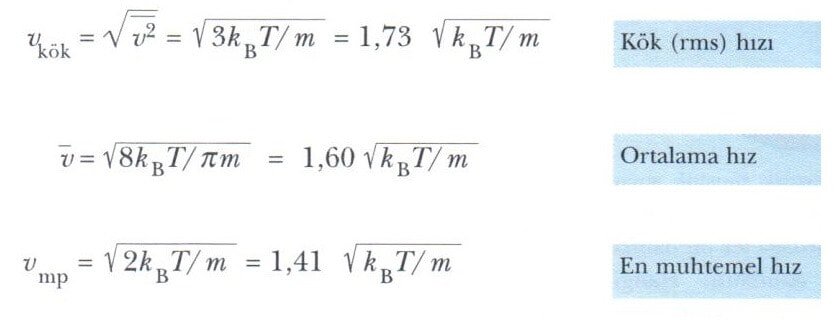
Bu eşitliklerden aşağıdaki sonuç elde edilir.

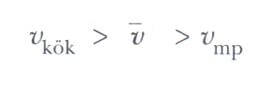
Şekil 2. N₂ moleküllerinin karakteristik hız dağılım eğrilerini göstermektedir. Sayfamızın en üstündeki N_v eşitliği kullanılarak, 300 К ve 900 К gibi değişik iki sıcaklıkta, farklı hızlardaki N_v değerleri hesaplanarak bu eğriler çizilmiştir. Sıcaklık artarken eğrinin sağa kaydığına dikkat ediniz. Bu beklendiği gibi artan sıcaklıklarla ortalama hızın arttığını gösterir. En düşük hız olasılığı sıfıra giderken, en yüksek hız sınırı sonsuza gittiği için, eğrilerin şekli simetrik değildir.