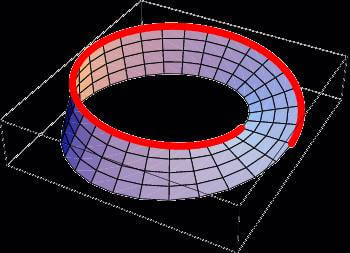
Matematiğin alt anabilim dallarından olan Topoloji, çok dikkat çekici nesnelerle uğraşmakta ve çalışmalar neticesinde insanın hayret ettiği nesneleri de bulmaya devam etmektedir. Topolojinin ne olduğu hakkında çok uzun konuşulabilir fakat biz bu yazı için uzay ve yüzey kavramlarının tanımlarını bilirsek yorum yapabiliriz. İlk olarak 1861 yılında Möbius Şeridi hakkında tanımlamaları veren, matematikçiler için ne anlam ifade ettiğini açıklayan Johann Benedict Listing olmasına karşın, ileri seviye araştırma alanına sokan ve üzerinde topolojik olarak çalışan August Ferdinand Möbiustur. Birçok insan tarafından bu nesne garip ve bir o kadar da ilginç karşılanmaktadır. Nasıl yaparız peki?
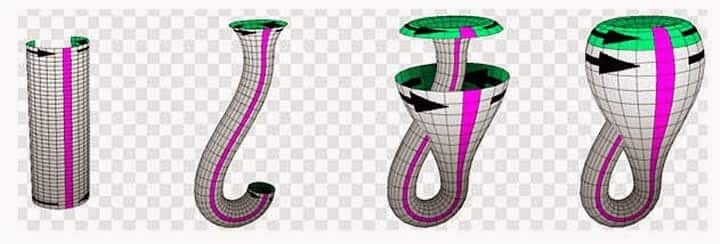
Elinize bir parça dikdörtgen biçiminde kağıt alın. Uçlarını silindir biçiminde değil de arka tarafına 180 derece bükerek ucu ile birleştirin. İşte şu yukarıdaki şekilde, birleştiriyoruz. Möbius şeridini ilginç kılan şey, herhangi bir hareketli bir noktadan diğer noktaya varması için bütün alanları taraması gerekir. Zaten A.F. Möbius yayınladığı makalesinde şeritlerin iki yüzü olmasına rağmen bu şeridin sadece bir yüzü olduğunu açıklamıştır.
Maalesef o yıllarda bu nesnenin bu kadar ünü yayılmamıştır. Ünlü sanatçı ve matematikçi M. Escher tarafından yaptığı resimlerin içinde bu şeridin mantığına uygun resimler yapmış ve resimlerin anlaşılması çok güç olmuştur.
Bu şeridin denklemleri ve matematiksel tanımları hakkında çok derinlere girmeden trigonometrik olarak tanımlayalım. Fakat biraz matematik bilmek gerekiyor. Birazcık…
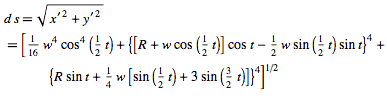
biçiminde bir parametrik denklem ile tanımlanır. Bu denklemler Matematik Bölümlerinde Analitik Geometri 2 dersinde kübik denklemler adlı konuda anlatılmaktadır. Bu denklem ile de şu şekil ortaya çıkmaktadır.