İstatistikteki temel fikirlerden bir tanesi daha küçük örneklere bakarak bütün hakkında bir fikir elde edebilmektir. Örneğin küçük bir nüfusa bakarak daha büyük nüfuslar hakkında bilgi almak. Ya da durun, seçimler hakkında kırsal bir yerin sonuçları doğrultusunda daha büyük yerlerin sonuçlarını tahmin edebilmek. Belki şu örnekte güzel olacaktır herhangi bir yerde yapılan köpürünün test güvenliğini başka köprülere de uygulayabilmemiz gibi. İşte burada matematiğin biraz daha özel bir alanı olan istatistiğin önemli bir yeri vardır. Bunların tüm sorumlulukları merkezi limit teoremi ile uygulanmaktadır.
Bu teoremin nasıl çalıştığını anlamak için şöyle birşey yapalım. Ankara’da dışarı çıkın ve gözünüze kestirdiğiniz 100 kişinin ağırlıklarını sorun ve bir kağıda not edin. Bu 100 kişi tamamlanınca da bir ortalama hesaplayın. Ortalamanız nedir? Şayet seçiminiz rastgele olduysa seçtiğiniz kişilerin ağırlık ortalaması Türkiye’nin ağırlık ortalamasına çok çok yakın olacaktır.
Bu deneyin geçerliliğini daha çok arttırmak adına 100 kişilik örneklem grubunu değiştirerek 3 kere yapın. Şimdi hesaplarınızı Türkiye’nin ağırlık ortalaması üzerinde deneyin. Sonuç? Sanki biraz daha yaklaştınız değil mi?
Fakat tek kişilik bir örneklem de 10 kilodan 150 kiloya kadar birçok değişken içereceğinden dolayı yaptığınız ölçüm sapması daha çok olan bir veri haline gelecektir. İşte merkezi limit teoremi burada devreye giriyor. Merkezi limit teoremine göre bir veride ölçülen ortalamanın limiti genel topluluğun oluşturduğu verilen ortalamasına eşdeğerdir. Bu belki cümlesel olarak çok basit gibi gözükebilir lakin hayatımızı tamamen tepe taklak attıran müthiş bir durumdur. Düşünün ki eliniz de bir veri var ve bu veri ile genelleme yapabiliyorsunuz üstelik dışarı çıkıp teker teker sormaya hiç gerek kalmadan. Hani matematik karşımıza nerede çıkıyor? Matematik günlük hayatta ne işimize yarıyor deniliyor ya daha ne işe yarasın ki?
Merkezi limit teorisi çan eğrisi gibi görünen o meşhur normal dağılım eğrisinin ortasında oluşan kardeş bir şekildir. Yani herhangi bir örneklem doğrultusunda 100 kişilik ekibin ortalamasına ulaşıp genelleme yapmamıza olanak sağlayacaktır.
Bu normal dağılımın varyansı, çan genişliği ile gösterilir. Bu ise örneklem boyutunun miktarına bağlıdır. Örneklem ne kadar büyük olursa varyans da o kadar küçük olur. Dolayısıyla, örneklem büyüklüğünüz yeterliyse (standard şartlarda 30 iken biz 100 seçtik) normal örnekleme dağılımının nispeten küçük varyansı, gözlemlediğiniz o normal dağılımın ortalamasına yakın olduğu anlamına gelir. (Çan çok dar hale gelir. )
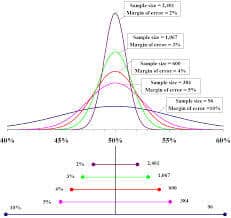
Bütün bunları kesin bir hale getirebilirsiniz yani gerçek ortalamanın, örnek ortalamanızın belirli bir mesafesinde olduğunu tam olarak söylemenize yardımcı olacaktır. Merkezi limit teoreminin belki de en önemli sonucu, sayısal sonucunuzu gerçek bir sonuca yakın hale getirmeniz için gereken örneklem sayınızı hesaplamanıza katkı sağlar. Matematiksel olarak açıklamasını ise pek yakında konuşacağız.

