MATLAB System Identification Toolbox ile Farklı Metodlar için Black Box Sistemin Modellenmesi

Sistemlerin verimli ve güvenli çalışması için kontrolörler hayati önem taşımaktadır. Bir sistemin kontrolör tasarımında ise öncelikle sistemin matematiksel ve fiziksel modeline ihtiyaç duyulur. Black box sistemlerde ise matematiksel olarak modelleme ancak system identification yakınsama yöntemleri kullanılarak mümkündür. Bu çalışmada black box bir sistem için Matlab System Identification Toolbox kullanılarak 4 farklı modelleme türü için 12 model elde edilmiş ve bunların kendi aralarında ve birbirleriyle karşılaştırılmaları yapılmıştır.

1. Giriş

Kontrolör tasarımında, artan güvenlik, verimlilik ve yüksek üretkenlik beklentilerini karşılamak için ilk adım sistem modelinin optimal şekilde oluşturulmasıdır. Bir kontrolörün verimliliği ve kalitesi, dizaynının temeli olan modelin sistemi temsil etme kabiliyetiyle doğru orantılıdır. Bu bağlamda sistem modellemesi üzerine çok sayıda çalışma mevcuttur.
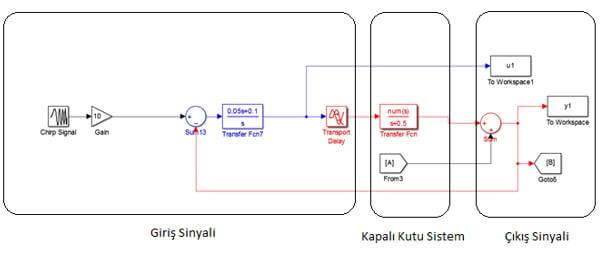
Modellenme açısından kontrol teorisinde sistemler üçe ayrılırlar. Bunlar White box, Gray Box ve Black Box sistemlerdir. Biz bu çalışmamızda şekil 1.’de verilen Black Box sistem üzerinde duracağız. Black box sistemler içeriği hakkında hiçbir bilgi sahibi olunmayan sistemlerdir. Bu sistemlerin modellenmesi ancak verilen giriş sinyallerine sistemin verdiği tepkiyi ölçerek ve bu ölçümleri zaman veya frekans düzleminde karşılaştırarak mümkündür.
Black Box için farklı lineer ve non-lineer sistem modelleme teknikleri mevcuttur. Bunların en bilinenleri ARX(Autoregressive model with exogenous inputs) ve ARMAXtır (Autoregressive moving average model with exogenous inputs).

Bu çalışmada Model 1’de verilen sistem kapalı kutu olarak alınmış ve elde edilen giriş ve çıkışlar kullanılarak ARX, ARMAX, Durum Uzay Denklemleri ve Transfer Fonksiyonu modellemesi yapılmıştır. Elde edilen sonuçlar karşılaştırılmıştır.

2. Black Box Sistemin Tanımlanması

Model 1’de Kapalı kutu bir sistem olması için  bir transfer fonksiyonu seçilmiş ve girişine chirp sinyal uygulanarak elde edilen sinyal rastgele verilen gürültü ile toplanmış ve çıkış sinyali elde edilmiştir. Elde edilen sinyaller Matlab ortamında işlenmiş ve 0.1 örnekleme zamanı ile identification data(iddata)’ya çevrilmiştir.  Şekil 2’de, elde edilen iddata ,Matlab System Identification Toolbox kullanılarak zaman düzleminde sistem tanılama için kullanılmıştır.

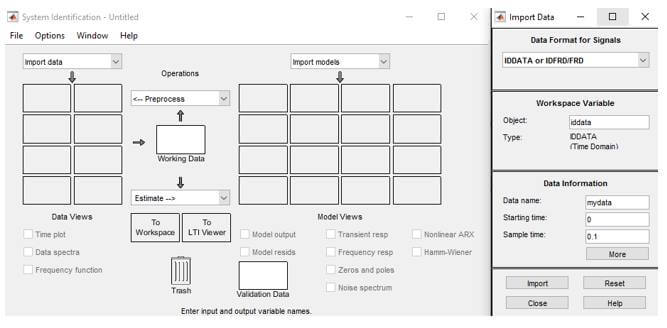
Buraya eklenen iddata SI içerisinde giriş ve çıkışların işlendiği bir grafik haline getirilip modelleme kısmına geçilmiştir. Modellemeyi yapmak için öncelikle şekil 3’te gösterilen listeden hangi modelleme türü istendiği seçilmiş ve buna göre modellemeler yapılmıştır.

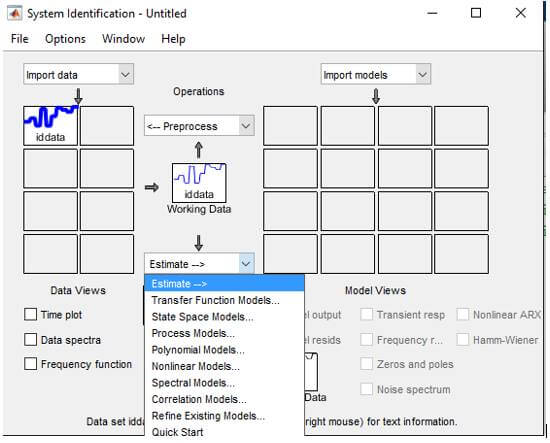
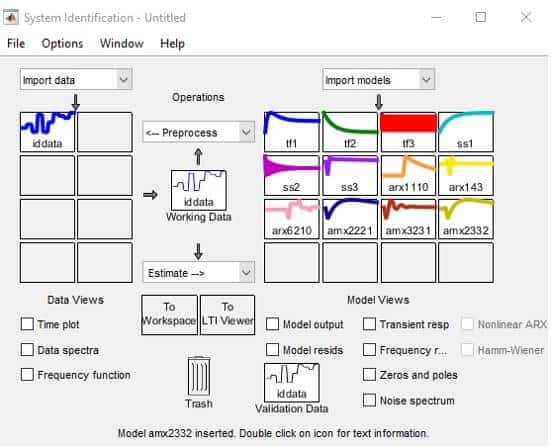
Yapılan çalışmada üçer adet ARX, ARMAX, Durum Uzay Modeli ve Transfer Fonksiyonu modeli belirlendi. Modeller belirlenirken girilen değerler ve elde edilen modellerin denklem ve verileri appendix B’de verilmiştir.

3. SI Toolbox ile Elde Edilen Sistem Modellerinin MATLAB/SIMULINK Ortamında Gerçeklenmesi

Model 2’de elde edilen transfer fonksiyonu modellerinin simulinkte gerçeklenmesi görülmektedir. 3 farklı transfer fonksiyonu aynı giriş sinyaline bağlanmış ve sistemlerin gerçek sistemle uyum oranları ve Mean Square Error(MSE) değerleri tablo 1’te verilmiştir. Tahmini sistem modelleri ile gerçek sistem modelinin karşılaştırılması figür 1 ve figür 2’de verilmiştir.

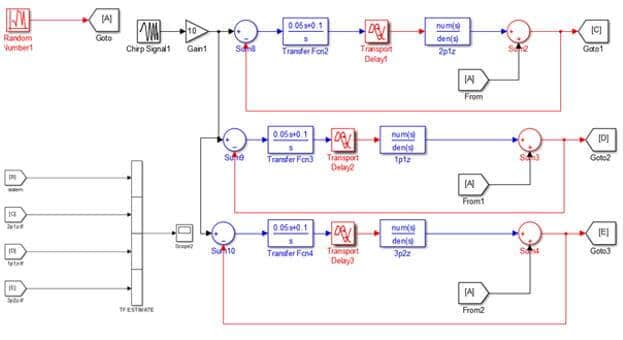
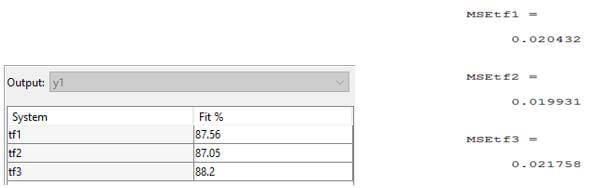
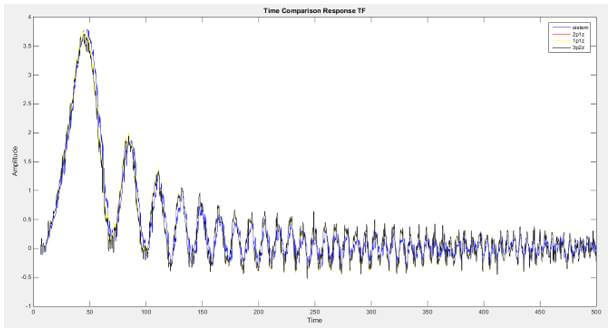
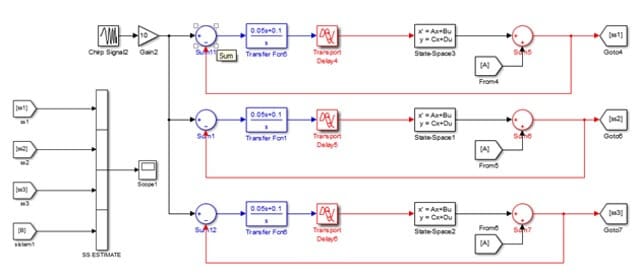
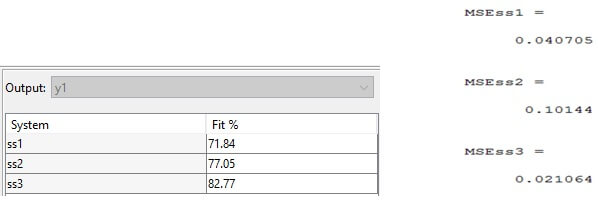
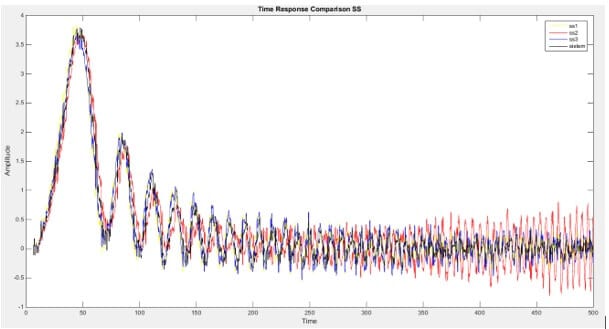
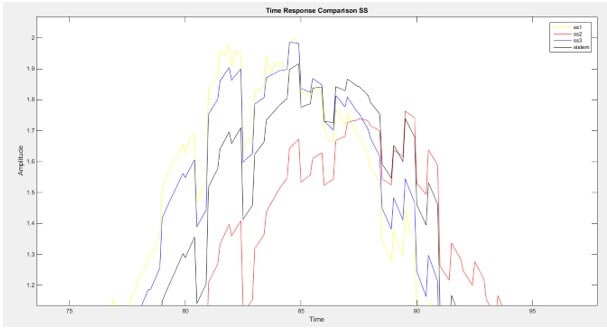
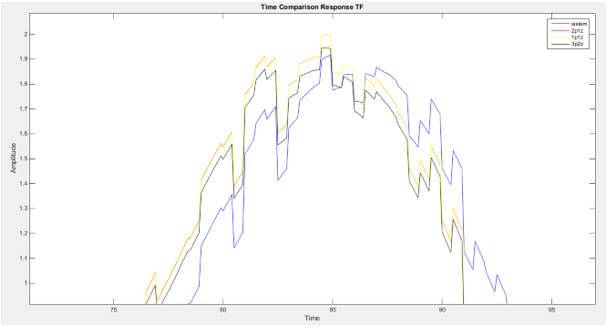Model 3’de elde edilen durum uzay modellerinin simulinkte gerçeklenmesi görülmektedir. 3 farklı transfer fonksiyonu aynı giriş sinyaline bağlanmış ve sistemlerin gerçek sistemle uyum oranları ve Mean Square Error(MSE) değerleri tablo 2’te verilmiştir. Tahmini sistem modelleri ile gerçek sistem modelinin karşılaştırılması figür 3 ve figür 4’te verilmiştir.

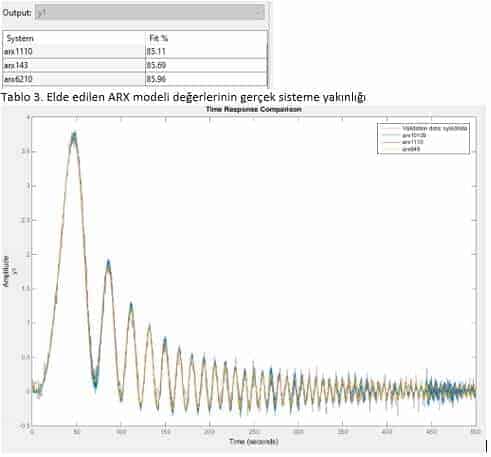
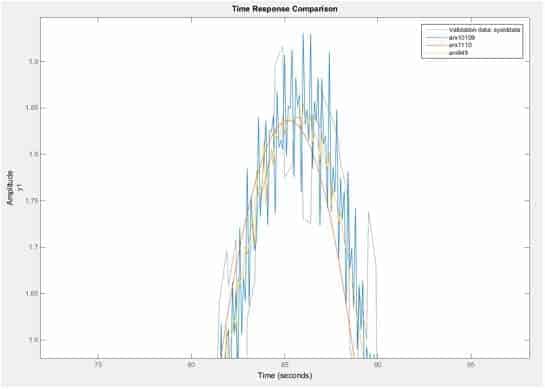
Sisteme ait ARX ve ARMAX modelleri ise matlab ortamına aktarılmış ve ‘compare’ komutu kullanılarak sistemle karşılaştırılmıştır. Karşılaştırma işlemi için kullanılan komutlar Appendix A’da verilmiştir.Tablo 3’te ve Tablo 4’te ise gerçek sistemle uyumluluk oranları verilmiştir.

ARX modelleri

arx(iddata,[1 1 10]);

Tahmini sistem modelleri ile gerçek sistem modelinin karşılaştırılması figür 5 ve figür 6’da verilmiştir.

ARMAX modelleri

armax(iddata,[2 2 2 1])

4. Sonuç

Bu çalışmada black box bir sistem için MATLAB SI Toolbox kullanılarak sistem modellenmesi gerçekleştirilmiştir. 4 farklı metod kullanılarak elde edilen sistemler karşılaştırılmış ve gerçek sistemle uyumluluk açısından tüm metodlar yaklaşık aynı sonucu vermiştir. Fakat MSE baz alınarak yapılan karşılaştırmada en küçük hata oranı 0.002606 olan ARX6210 modelinde görülmüş olup bu oran özellikle Transfer Fonksiyon Modellemesi ve Durum Uzay Modellemesine oranla çok küçüktür. Çalışmanın sonucunda ARX6210 modelinin en uygun sistem modeli tahmini olduğuna kanaat getirilmiştir.

APPENDIX A

SİSTEMDE KULLANILAN MATLAB KODLARI

Elde edilen sistemlerin karşılaştırılması:

compare(sysiddata,tf1,tf2,tf3)   %elde edilen transfer fonksiyonların sistem ile karşılaştırılması
compare(sysiddata,ss1,ss2,ss3)   %elde edilen state denklemlerinin sistem ile karşılaştırılması
compare(sysiddata,arx10109,arx1110,arx649)   %elde edilen arx modellerin sistem ile karşılaştırılması
compare(sysiddata,amx2221,amx3231,amx3432)   %elde edilen armax sistem ile karşılaştırılması

TF ve SS sistemler için MSE hesaplanması

%Elde edilen tf sistemler için Mean Square Error uygulaması

Xs=sistem
Xt1=tf1data
Xt2=tf2data
Xt3=tf3data
MSEtf1 = mean(abs(Xs-Xt1).^2)
MSEtf2 = mean(abs(Xs-Xt2).^2)
MSEtf3 = mean(abs(Xs-Xt3).^2)
%Elde edilen ss sistemler için Mean Square Error uygulaması
Xs1=ss1data
Xs2=ss2data
Xs3=ss3data
MSEss1 = mean(abs(Xs-Xs1).^2)
MSEss2 = mean(abs(Xs-Xs2).^2)
MSEss3 = mean(abs(Xs-Xs3).^2)
Not: Arx ve Armax modellerin MSE değerleri identification metninde bulunmaktadır.

APPENDIX B

System Identification Toolbox tarafından elde edilen durum uzay denklemleri ve transfer fonksiyonları

1. Transfer Fonksiyonları

2p1z (2 POLE 1 ZERO için TF modeli)
Num= [-0.476353671421401 6.397766065314639]
Den= [1 15.344079263073349 31.970168733981367]
2p1z=tf(num,den)

1p1z (1 POLE 1 ZERO için TF modeli)

Num= [-0.043601285638000 0.431239839534593]
Den= [1 2.153542668066677]
1p1z=tf(num,den)

3p2z (3 POLE 2 ZERO için TF modeli)

Num= [-0.726695674821713 7.952719362782554 0.062250378797647]
Den= [1 18.832135136556676 40.191974995914880 0.35905118632259]
3p2z=tf(num,den)

2. Durum Uzay Denklemleri

ss1 ( 5 state)

A= [-32.9962967102414 -14.1545595235487 9.06676591010389 4.36814796941688 -0.00197915128892112;11.9126643285912 3.80911940784745 6.95137642851109 0.0746926989869915 -0.202802065140696;-25.2262529636876 -15.5763039423476 2.23762729800870 -1.53945940816579 0.543378898143835;-13.2837323187939 -3.99718687845417 3.17619898281997 0.429276191519736 -7.37048281606916;-15.2687618716247 -3.31391291073968 1.31129913435271 9.32498017055930 -4.09328183551397]
B= [31.312441980151170;-4.84130827898040; 27.313229583267630; 14.424967114963255;9.779791239848384]
C= [4.474335100740385 -2.053252140551946 -1.119892906803536 0.240186155716129 -0.125573245808367]
D=0

ss2 (3 state)

A= [-1.576250387050179 -1.019889745148532 0.910274865683111; 0.200831755125586 0.169224011270027 1.339323791501261;-1.660793619399005 -1.844548705571788 -0.013848286787149]
B= [0.356232380110288;0.115271132329653;0.371552795712823]
C= [5.567202736361282 -1.927488965508075 -0.667963169965329]
D=0

ss3 (Discrete SS model) (2 state)

A=  [0.451212655797023 0.719911341724888;0.418573695462092      -0.405526815144465]
B= [0.025520596133929;-0.062083447196878]
C= [-6.890827909653144 -1.333756827402173]
D=0