Manyetik Alanda Enerji

Bu yazımız manyetik alanda enerji hakkında olacak ve konuyu daha iyi anlamamız için manyetik alanda enerji ile ilgili soru çözeceğiz.

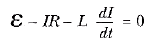
İndüktörde indüklenmiş olan emk, bir bataryanın ani akım oluşturmasını engellediği için, batarya, bir akım oluşturmak için indüktöre karşı iş yapmalıdır. Batarya tarafından sağlanan enerjinin bir kısmı dirençte iç enerji olarak görünür, geri kalan enerji ise indüktörün manyetik alanında depolanır. Eşitlik 1 deki her terimi I akımı ile çarpıp ifadeyi yeniden düzenlersek

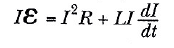
buluruz. Bu denklem; bataryanın sağladığı birim zamandaki Iε enerjisinin, dirence birim zamanda verilen I²R enerjisi ile indüktörde birim zamanda depolanan LI(dI/dt) enerjisinin toplamına eşit olduğunu ifade eder. Böylece, Eşitlik 1, basitçe enerjinin korunumu ifadesidir. Herhangi bir anda indüktörde depolanan enerjiyi U ile gösterirsek, indüktörde depolanan enerji hızı için dU/dt oranı aşağıdaki gibi yazılabilir:

İndüktörde depolanan toplam enerjiyi bulmak için, bu denklemi dU = LIdI şeklinde yeniden yazıp integralini alabiliriz:

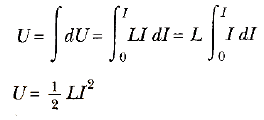
Burada L bir sabit olup, integral dışına alınmıştır. Bu ifade, akım I değerinde olduğu zaman, bir indüktörün manyetik alanı içinde depolanan enerjiyi tem­sil eder. Bunun, biçim olarak verilen bir kondansatörün elektrik alanı içinde depolanan Q²/2C enerji ifadesine benzediğine dikkat edilmelidir. Her bir durumda, bir alan oluşturmak için bir enerjiye ihtiyaç du­yulduğu görülür.

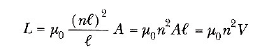
Manyetik alanın enerji yoğunluğunu da belirleyebiliriz. Basitlik için, indüktansı Eşitlik 4 ile verilen bir solenoid düşünelim:

L = μ₀n²Al

Solenoidin manyetik alanı Denklem 1

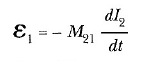
B = μ₀nl

ile verilir. L ve I = B/μ₀n, Eşitlik 3 te yerine konulursa

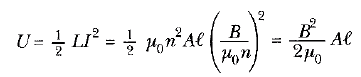
bulunur. Al solenoidin hacmi olduğundan, indüktörü çevreleyen manyetik alan içinde birim hacim başına depolanan enerji aşağıdaki eşitlikle verilir:

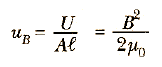
Bu ifade, solenoid özel durumu için türetilmiş olmasına karşın, manyetik alanın var olduğu herhangi bir bölge için de geçerlidir. Eşitlik 6 nın, biçim bakımından, Elektrik alanda birim hacminde depolanan enerji olan u_E = (1/2)ε₀E² eşitliğine benzediğine dikkat edilmelidir. Her iki durumda enerji yoğunluğu, alanın şiddetinin karesiyle orantılıdır.

Manyetik Alanda Enerji İle İlgili Soru

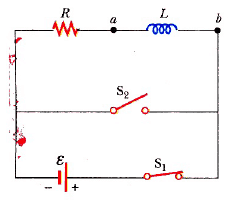
Şekil 1 deki RL devresini göz önüne alın. Burada, t = 0 da, S₁ anahtarı açıldığı anda S₂ anahtarı kapa­tılmıştır. Üst halkadaki akımın I = I₀e^-t/τ ifadesine uygun olarak zamana göre üstel bir biçimde azaldığı hatırlanmalıdır. Buradaki I₀ = ε/R devredeki ilk akım ve т = L/R zaman sabitidir. İndüktörün manyetik alanında, başlangıçta depolanmış olan tüm enerjinin, akımı sıfıra doğru azaldıkça, dirençte iç enerji olarak göründüğünü gösteriniz.

Çözüm Dirence enerjinin verilme hızı olan dU/dt oranı (güç olarak bilinir) I²R ye eşittir. Burada I ani akımdır:

Dirence verilen toplam enerjiyi bulmak için, bu ifadenin t = 0 dan t= ∞’a kadar integrali alınır. (Akımın sıfıra ulaşması sonsuz zaman aldığı için, üst sınır olarak ∞ alınmıştır.):

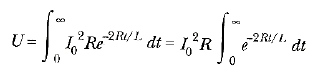
elde edilir. Belirli integralin değeri L/2R (Bu hesaplamanın gerçekleştirilmesi, bu örneğin sonundaki alıştırmada, öğrenciye bırakılmıştır.) Böylece U aşağıdaki değeri alır:

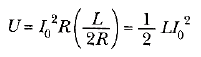
Bunun, ispatlamaya çalıştığımız, Eşitlik 5 ile verilen, indüktörün manyetik alanında depolanan ilk enerjiye eşit olduğuna dikkat ediniz.

Bu yazımızda sizlere manyetik alanda enerji konusunu anlattım. Diğer yazımızda görüşmek üzere.