Kaos Teorisi dediğimiz temel yapının ilk çıkış noktası olarak bir hikayeden başlayalım. Benoit Mandelbrot (1924 – 2010) bir bilim insanı ve matematikçidir. Genellikle çalıştığı nokta “Fraktal” olarak adlandırılan matematiksel ahenkler üzerinedir. Hayatını da bu çalışmalara adamıştır. Özellikle kendi adıyla anılan “Mandelbrot Kümesi” ise üstünde çalıştığı çok özel bir alandı. Peki Mandelbrot kümesi neyin nesidir?
1950’li yıllarda Mandelbrot IBM adında bir şirkette matematikçi olarak çalışırken bilgisayarların bazı hatalar verdiğini gözlemlemiştir. Bu hataların zaman skalerlerini ay, hafta, gün, saat, dakika, saniye, salise şeklinde ayırdığı zaman tekrar eden bir düzen görmüştür. İşte tam bu noktada fraktal diye nitelendirdiğimiz yapıların olduğunu fark etmiştir. Sadece bir merak sonucu diretilen bir duygu matematiğin apayrı bir dalının oluşmasını sağladı. Dikkat edilmesi gerekiyor ki fraktal ismi yıllar sonra (20 yıl sonra) farklı bir matematikçi tarafından Mandelbrot’un çalışmalarının ürünü olduğundan dolayı ona ithafen verilmiştir. (Aşağıdaki bahsedeceğiz)
Karmaşık sayılar düzleminde f(z) olarak tanımlanan fonksiyonun z’nin karesi alınıp herhangi bir gelişigüzel sabitin eklenmesiyle oluşan kümeye “Mandelbrot Kümesi” denir. Bu kümenin kompleks düzlemde grafiği,
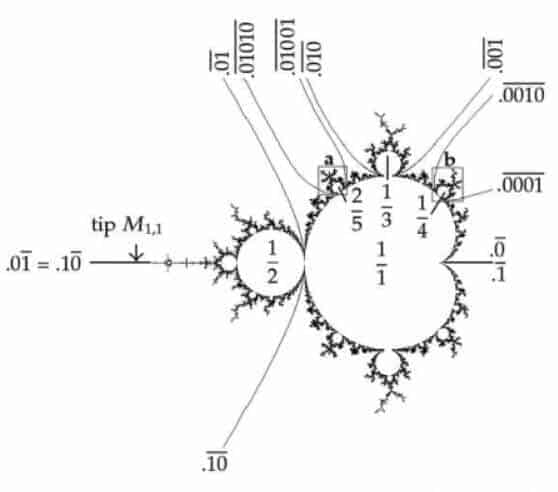
şeklindedir. Buradaki sabitimiz olan “C” ifadesi kümenin değer kümesini yani büyüklüğünü arttırmaya yardımcı olmaktadır. Grup teorisi olarak önemli bir yeri olan Cebir’in alt dalının da konusu olan bu kümeler PSL (2,C) grubunun bir üyesidir. Belki araştırma yapmak isteyenler bir cebir kitabı açıp (ileri düzey) okuyabilir. Daha sonraları bu yukarıdaki matematiksel ifade bilgisayar yardımıyla aşağıdaki düzleme aktarılmıştır.
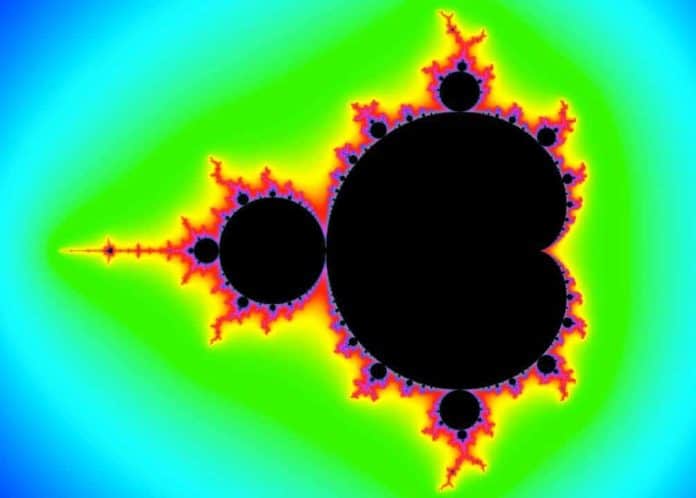
Buradaki değerler kafamızı hiç karıştırmasın. Bu değerler bizlerin karşısına analitik geometri dersi almış (üniversite düzeyde) kişilerin anlamasına biraz olsun yardımcı olacaktır. Sağ tarafta bir kardiyoid p=1 ve sol tarafta ise p=2 merkezlidir. Durun bunlar güzel değil. Hemen bilgisayar ekranında hesaplandığında karşımıza gelen tertemiz bir Mandelbrot kümesi alalım.
Şimdi şu siyah noktalara bakalım. Uç kısımlarda gördüğümüz varya… Ne görüyorsunuz? Sanırım gözünüz yapay zekaya ait değilse hiçbir şey göremeyeceksiniz. Mandelbrot kümesini meşhur yapan şey bu gördüğümüz fotoğraf değil. Siyah noktalardan ötesi… Benoit Mandelbrot bu siyah noktaların ötesinde birşeyler olduğunu biliyordu fakat bir türlü gösteremiyordu. Bunun iki nedeni vardı: Birincisi akademik olarak bazı sorunlar, diğeri ise teknolojinin yetersiz olması…
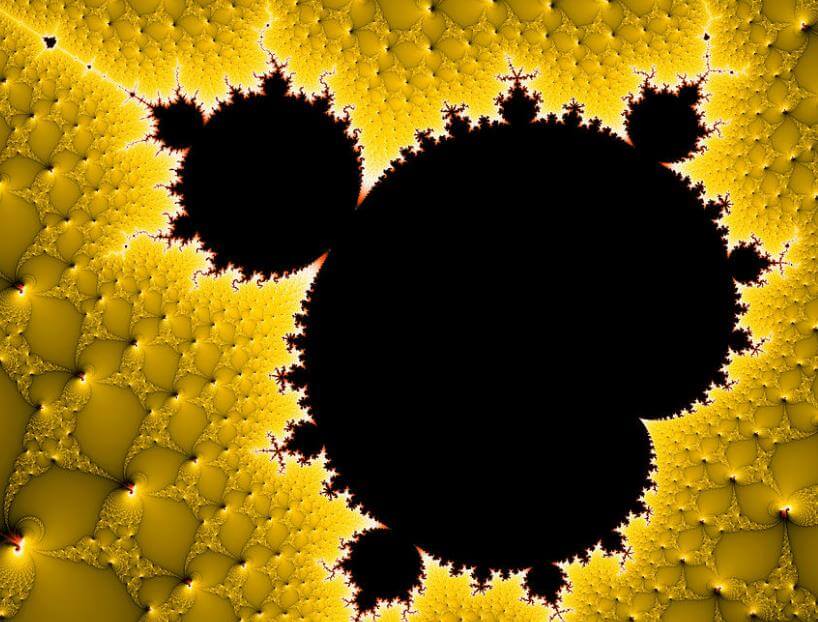
Esrarengiz döngü 1978 yılında B. Mandelbrot ile Robert Brooks ve Peter Matelski‘nin de yardımıyla bu siyah noktaların bir sarmal şeklinde sonsuza dek gittiğini hatta türevlenebilir olduğunu göstermişlerdir. İşte yukarıda da bahsettiğimiz gibi asıl fikir sahibinin ve en önemli çalışmaların Mandelbrot’a ait olduğu düşüncesi ile bu ikili makalelerinde ona gönderme yapmışlardır. Bakın şöyle bir yakınlaşalım, neler göreceğiz?
Güzel bayağı yakınlaştık. Şimdi ahtapot kolları gibi şeyler görüyorsunuz değil mi? O kollardan devam edelim. Bu kollar sonsuza kadar devam etmektedir. Bakın hemen yakınlaştıralım.
Kollara doğru yönelmek istiyorum. Biraz daha büyütüp kolların şekline bakalım.
Olayların hepsi işte bu noktada başlamaktadır. Karmaşık düzlemde alınan noktaların türevlenebilir kısmı sonsuza dek devam etmektedir. Üstelik kollardan büyütmeye devam ettiğinizde ilk düzlemde karşımıza çıkan görüntü kümesini elde edeceksiniz. İşte fraktal geometri bu olayla patlak verdi. Bakın yakınlaştırdığımız zaman – yakınlaştırırken bir noktaya odaklanın ve o nokta üzerinde devam edin – karşımıza çıkacak şekil şöyledir.
Çok az da yukarıdaki matematiksel denklemden bahsetmek istiyorum.
![]()
şeklinde gösterilen ve karmaşık düzlemin bir fonksiyonu olarak tanımlanan bu denklem c sayısının değişmesine göre şeklin şişman ya da zayıf olmasını sağlar. Yani şunu söylemek istiyoruz. Şekiller çift taraflı hale gelecektir. Bu da bir fraktal oluşturacaktır fakat bazı noktalarda türev almak sıkıntılı hale gelecektir. Bu tür c sabiti değiştirilmiş biçimler de yine Mandelbrot Kümelerinin içine dahil edilmektedir.
Ülkemizde ise bu alanda çalışan önemli bilim insanlarından Prof. Dr. Sinan Canan fraktal geometrinin önemli temsilcilerinden biridir. Faydalı ve bizlere ufuk açan çalışmalarını takip etmekte fayda olacağını dünüşüyoruz. Doğada matematik nerede var gibi sorulara maruz kalırsak lütfen çekinmeden fraktal geometri konusunu açalım. Süsleme sanatı ise fraktal geometri ile akrabalık göstermektedir. Bugün kullanılan süsleme sanatında göz ahengi oluşturmak için fraktallara sıkça danışılmaktadır.