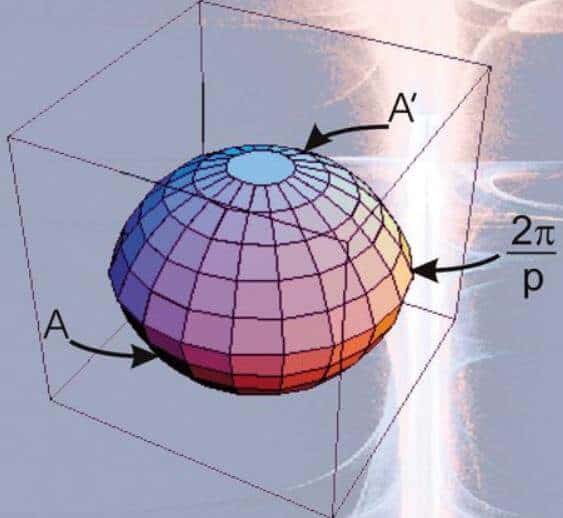
Matematikte çözemediğimiz sorular fizikle birleşince işin içinden çıkılmaz bir hal almaktadır. Özellikle genel görelilik – uzay – zaman gibi kavramların daha da yakından anlaşılması ile fizikçiler ve matematikçiler kardeşliğini ilan ettiler. Uzayın matematikten ve fizikten ayrı düşünmek büyük günah olsa gerek. Gözlerinizi kapatın ve kendinizi bir dondurma külahında olduğunuzu düşünün. Ama karıncadan 100.000 kat daha küçük daha olun. Evet o küresel kıvrımı düşünebilir musunuz? Düşünemediniz değil mi? Bu işte geometrik yanılmanın kendisidir.
1950’li yıllarda geometri dünyasını saran “Geometrik Görünmezlik” çalışmaları insanların biraz demek az kalacağından aşırı heyecanlı yıllar geçirmesine sebep olmuştur. Bu akılcı ve felsefik matematik oluşumu tek katlı yüzeylerin sonlu boyutlardan dönüşümünü konu alır. İntegral yüzeyleri ile hesaplanan tüm tek ya da sonsuz katlı yüzeylerden farklı “Laboçhevski pütürleri” geometrik dizilerin tek katlı uygulamalarını gösteriyordu. Lakin sonlu bir hacme sahip bu yüzeylerin hesaplanması olanaksızdı. Nasıl yani? Yukarıdaki dondurma külahında mısınız hala? Orada kalın ve önünüze bakın. Peki ne görüyorsunuz. Uçsuz bucaksız bir alan… İşte Lobachevsky de bunu söylüyor; “Eğer sonlu bir çok katlının içinde minik bir nesne iseniz bu alan sonsuz alandır. Alanın hesaplanması ise integral ile hesaplanamaz”
Aynı şey dünyada yaşayan insanlar içinde geçerli değil mi? İlk zamanlarda insanların dünyanın düz olduğunu kabul etmesinin tek sebebi “Lobachevsky pütürü”dür. Aslında matematik bilmeyenlerin dünyanın düz olduğunu kabul etmesi kadar normal bişey yoktur! Eliptik yüzeylerin sınıflandırılmasından sonra 1900’lü yıllar Paris konferansında Hilbert aksiyomları ile bir nebze olsun anlaşılmıştır. Evet bir takım matematikçi dünyanın düz olduğunu ölene dek kabul ediyordu. Fakat bu konferanstan sonra bu fikirlerinden hızlı bir dönüş yapmışlardır.
Özellikle matematik ile yapılan çalışmaların bir çoğu bugün uzay ve evren kavramlarının daha net anlaşılmasına yardımcı oldu. Einstein’ın B. Riemann için söylediği tek cümle aslında her şeyi kanıtlar nitelikteydi. “Eğer Riemann olmasaydı yaptığım çalışmaların hepsi askıda kalırdı.”
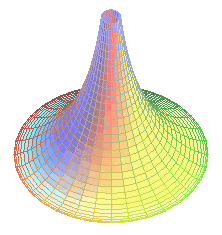
Riemann geometrisini duyduğumuzdan eminiz! Fakat tam ters özelliklere sahip Öklid dışı geometrinin başka bir versiyonu olan hiperbolik geometrinin mucidi Lobaçevski Öklidin çok uzun yıllarca sarsılmaz tahtına bir darbe vurmuştur. Öklid geometrisindeki ilk dört aksiyom gerçekten çok önemli bir aksiyomdur. Şuanda sarsılmaz olarak kabul edilmesine lakin 5. aksiyomda bir gariplik vardı. Bazı matematikçiler bunun ispatlanması gerektiğini söylüyordu. Lobaçevski de bunlardan biriydi. Rus matematikçi ilk dört aksiyomu kullanarak öklid dışı geometriye yeni bir heyecan getirmiştir. Lobaçevski ise son aksiyomu değiştirerek aynen şöyle bir cümle kullandı. “Bir doğruya dışından alınan bir noktadan en az iki paralel çizilebilir.” Bu çok iddialı bir cümleydi. Hak ediyordu da zaten. Hiperbolik geometri olarak matematik dünyasına geçen bu farklı uğraş alanı, iki tane uzayın uç uca geçmesi ile ve bu uçlarının gitgide incelmesi ile oluşur ki bunlar aynı şunlara benzemektedir. Sanki bir zurna misali…
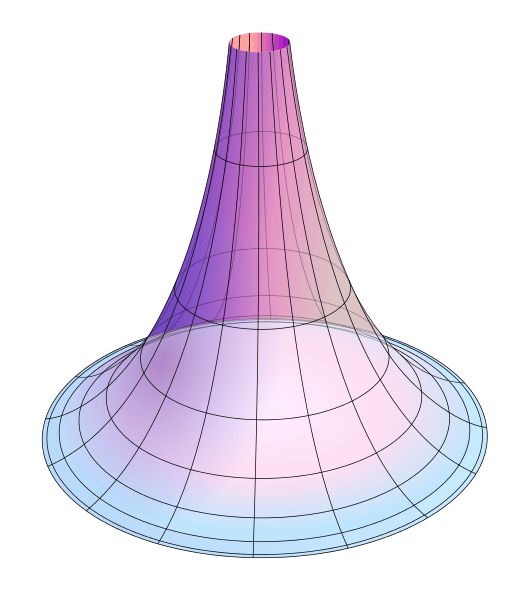
Hatırlarsanız Riemann geometrisinde herhangi üç noktanın oluşturduğu üçgenin iç açıları toplamı 180 dereceden büyüktü fakat Labocevski geometrisinde eğriden alınan üç noktanın oluşturduğu üçgenin iç açıları toplamı ise 180 dereceden küçüktür.
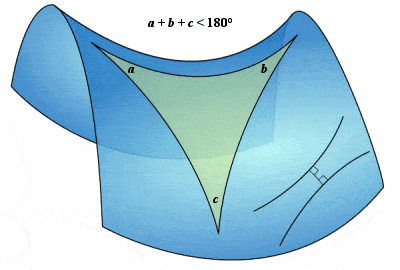
Fazla derinlere gitmektense nerede kullanılıyor diye soralım kendimize? Bugün astronomi ile ilgilenen Nasa çalışanlarının en çok bildiği konulardan bir tanesidir aslında Labocevski geometrisi.. En basit olarak evrendeki karadelikler sadece bu geometrinin sayesinde bulundu nokta…
Bize “Üçgenin iç açıları toplamı kaç dereceydi” şeklinde bir soru geldiğinde hemen şu cevabı verelim, “Hangi geometride?”