Kuvvet Kavramı ve Özellikleri

Herkes, günlük gözlemlerinden kuvvet kavramı hakkında az çok bir fikre sa­hiptir. Bir cismi ittiğiniz veya çektiğiniz zaman onun üzerine bir kuvvet uygu­larsınız. Bir topa vurduğunuzda veya fırlattığınızda da ona bir kuvvet uygular­sınız. Bu örneklerdeki kuvvet kelimesi, kas gücü sonucu cismin hareketindeki değişmeyle ilişkilidir. Kuvvetler, her zaman bir cismin hareket etmesine neden olmazlar. Örneğin bu kitabı okumak üzere oturduğunuzda, sizin vücudunuza çekim kuvveti uygulandığı halde siz durgun kalırsınız. Bir kaya parçasını itersiniz, fakat onu hareket ettiremeyebilirsiniz.

Ayın Dünya etrafındaki yörüngesinde dönmesini sağlayan kuvvet (varsa) nedir? Newton’un bu tür sorulara cevabı şudur: Cismin hızındaki değişmeye ancak bir kuvvet neden olabilir. O halde, düzgün doğrusal hareket (sabit hız­la) yapan bir cisme, hareketin devamı için kuvvet uygulanması gerekmez. Dünyanın çevresinde hemen hemen dairesel yörüngede döndüğü için Ay nı hızı sabit değildir. Hızdaki bu değişmeye, Dünya’nın Ay üzerine uyguladığı kuvvetin sebep olduğunu şimdi biliyoruz. Hızdaki değişme ancak bir kuvvet uygulanmasıyla mümkün olabileceğinden, cismin ivmelenme nedeninin kuv­vet olduğunu düşünebiliriz. Bu bölümde, bir cismin üzerine uygulanan kuvvet ile cismin ivmesi arasındaki ilişkiyi inceleyeceğiz.

Şimdi, bir cisme aynı anda birden fazla kuvvetin uygulandığı hali gözönüne alalım. Bu durumda, cismin üzerine etki eden net kuvvet sıfırdan farklı olursa cisim ivmelenecektir. Bir cismin üzerine etki eden net kuvvet o cismin üzerine uygulanan kuvvetlerin tamamının vektörel toplamı olarak tanımlanır (Net kuvvet yerine, toplam kuvvet, bileşke kuvvet, dengelenmemiş kuvvet terimleri sık sık kullanılır). Net kuvvet sıfır ise ivme de sıfırdır ve cismin hızı değişmez. Yani, cisme uygulanan net kuvvet sıfır ise o cisim ya duracak ya da sabit hızla hareket edecektir. Cismin hızı sabit veya cisim durgun halde iken, o cismin dengede olduğu söylenir.

Bir yayı Şekil 1a da görüldüğü gibi çekerseniz yay gerilir. Şekil 1b de görüldüğü gibi bir arabayı sürtünme kuvvetini yenecek bir kuvvetle çekerseniz araba hareket edecektir. Son olarak bir futbol topuna Şekil 1c de görüldü­ğü gibi bir tekme vurursanız, top hem şekil değiştirir hemde hareket eder. Bunların hepsi temas kuvvetleri olarak adlandırılan kuvvet sınıfına örnektir. Ya­ni, bu kuvvetler, iki cismin arasındaki fiziksel temas (değmenin) sonucu orta­ya çıkan kuvvetleri simgelerler. Değme kuvvetlerine ait diğer örnekler; kapalı kaptaki bir gazın çeperlere uyguladığı kuvvetler (moleküllerin duvarlara çap­ması sonucu doğan kuvvetler) ve bizim ayaklarımızın döşemeye uyguladığı kuvvetlerdir.

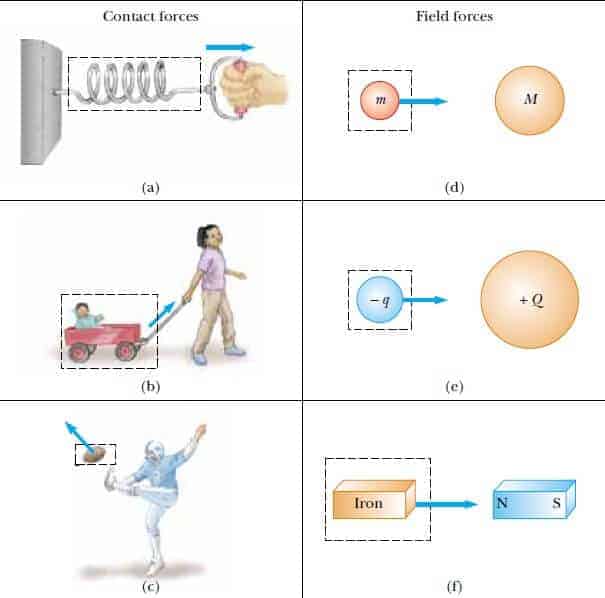
Şekil 1: Çeşitli cisimlere uygulanan kuvvet örnekleri. Her bir durumda, çerçeve içine alınmış cisim veya parçacığa bir kuvvet uygulanmaktadır. Dış çevre, çerçevelenmiş bölgedeki cisme bir kuvvet uygular.

Alan kuvvetleri olarak bilinen diğer bir kuvvet sınıfında, cisimler arasında değme (fiziki temas) yoktur. İki cisim boş uzay içinde etkileşir. Şekil 1d de görülen iki cisim arasındaki kütle çekim kuvveti, bu sınıfa bir örnektir. Bu kuvvet, cisimlerin dünyaya bağlı kalmasını sağlar. Bizim güneş sistemimizdeki ge­zegenler, kütle çekim kuvvetlerinin etkisi ile güneşe bağlı kalırlar. Alan kuv­vetlerinin diğer genel bir örneği, Şekil 1e de görülen elektrik yüklerinin bir­birlerine uyguladıkları kuvvetlerdir. Yükler, bir hidrojen atomunu oluşturan proton ve elektron olabilir. Alan kuvvetlerinin üçüncü bir örneği, Şekil 1f de görülen bir çubuk mıknatısın demir çubuğa uyguladığı kuvvettir. Atom çekir­değini dağılmadan bir arada tutan kuvvetler de alan kuvvetleridir, fakat kısa menzillidir. Bu tür kuvvetler, parçacıklar arasındaki uzaklıklar 10^-15 m merte­besinde olduğu durumlarda baskın olurlar.

Newton dahil olmak üzere eski bilim adamları için, bir birleriyle temas halinde olmayan iki cismin, birbirlerine kuvvet uygulamasını anlamak zordu. Bu kavramsal problemi çözmek için Mıchael Faraday (1791-1867) alan kavramını ortaya atmıştır. Bu yaklaşıma göre, 1 cismi 2 cisminin yakınındaki bir P noktasına konulunca, 1 cismi 2 cismi ile P de var olan çekim alanı vasıtası ile etkileşir. P deki çekim alanı, 2 cismi tarafından oluşturulmuştur. Benzer şekilde 2 cisminin bulunduğu konumda da 1 cismi tarafından bir çekim alanı oluşur. Gerçekte, bütün cisimler uzayda kendi çevrelerinde çekim alanı oluştururlar.

Alan kuvvetleri ile değme kuvvetleri arasındaki farkın yukarıdaki açıkla­maların ortaya koyduğu kadar keskin olmadığını belirtmeliyiz. Gerçekte, ato­mik seviyede değme kuvvetleri, yükler arasındaki elektrik kuvvetlerinden kaynaklanır ve bunlar Şekil 1e de gösterilen çeşitte alan kuvvetleridir. Böyle olma­sına rağmen, gelişmiş makroskopik modellerde her iki sınıflandırmayı da kul­lanmak uygun olmaktadır. Bunun yanında doğada var olan temel kuvvetler. (1) Kütle çekim kuvvetleri; iki cismin kütlelerinden dolayı birbirlerine uyguladık­ları çekim kuvvetleri. (2) Elektromanyetik kuvvetler; durgun veya hareketli iki yüklü parçacığın yüklerinden dolayı birbirlerine uyguladıkları itme veya çek­me kuvvetleri. (3) Atom-altı parçacıklar arasında görülen, şiddetleri büyük çe­kirdek kuvvetleri. (4) Zayıf nükleer kuvvetler; (zayıf etkileşmeler olarak adlan­dırılırlar) belli radyoaktif bozun malarda ortaya çıkan kuvvetlerdir. Klasik fizik­te, sadece kütle çekim ve elektromanyetik kuvvetlerle ilgileneceğiz.

Bir Kuvvet ‘in Şiddetinin Ölçülmesi

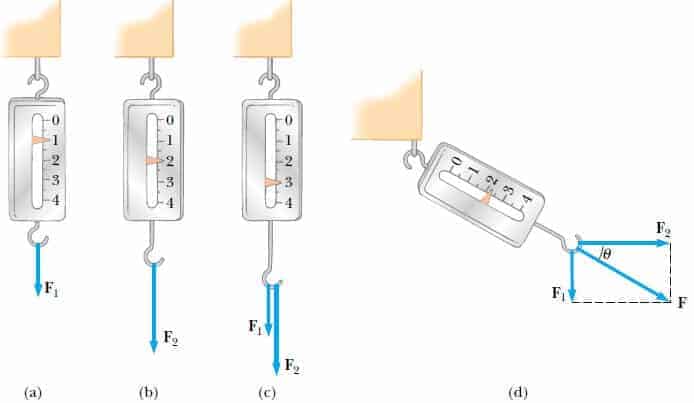
Şekil 2:Bir yaylı kantar ile bir kuvvetin vektörel özelliğinin denenmesi (a) Aşağı yönelmiş bir F₁ kuvveti yayı 1 cm uzatır, (b) Aşağı yönelmiş F₂ kuvveti yayı 2 cm uzatır, (c) F₁ ve F₂ kuvvetleri aynı anda aşağı yönde uygulandığı zaman yay 3 cm uzar, (d) F₁ kuvveti aşağı yönde, F₂ kuvveti yatay olarak uygulandığı zaman bu iki kuvvet yayı uzatır.

Bir yayda gözlenen şekil değişimini, kuvveti ölçmek için kullanmak uygundur. Şekil 2a da görüldüğü gibi üst ucundan tutturulmuş bir yaya düşey doğrul­tuda bir kuvvetin uygulandığını varsayalım. Kuvvet uygulanınca yay uzar ve öl­çek üzerindeki göstergeden kuvvet ölçülür. Göstergenin 1.00 cm uzama gös­terdiği F₁ kuvveti birim kuvvet olarak tanımlanarak yayı ölçekleyebiliriz (Kuv­vet vektörel bir nicelik olduğundan F₁ koyu yazıldı). Eğer şimdi 2 birim şidde­tinde bir F₂ kuvveti Şekil 2d de görüldüğü gibi uygulanırsa, gösterge 2.00 cm ye hareket eder. Şekil 2c; aynı anda iki kuvvetin etkisinin tek tek uygulanma­ları halindeki etkilerinin toplamına eşit olduğunu gösterir.

Şimdi Şekil 5.2d de görüldüğü gibi F₁, aşağı, F₂ yatay olarak aynı anda uy­gulanmış olsun. Bu durumda gösterge

yi gösterir. Yayda aynı uzamayı meydana getirebilecek tek bir F kuvveti Şekil 5.2d de görüldüğü gibi F₁ ve F₂ kuvvetlerinin vektörel toplamıdır. Büyüklüğü

birim ve doğrultusu 0 = arctan (-0,5) = -26,6⁰ dir. Kuvvetler vektörel nicelikler olduğundan, bir cisme etki eden bileşke kuvveti elde etmek için vektörlerin toplanması kuralım uygulamalıyız.