Kütle Çekim Potansiyel Enerjisi kavramını, yani, parçacığın konumuna eşlik eden enerjiyi ortaya koyduk. Çekim potansiyel enerjisi yalnızca çekim kuvvetinin sabit olduğu durumda; parçacık, Dünya yüzeyinin yanındayken geçerli olduğunu vurguladık. İki parçacık arasındaki kuvvet 1 / r ile değiştiğinden, Dünya yüzeyinin yakınında olma kısıtlaması olmaksızın geçerli olan daha genel bir potansiyel enerji fonksiyonunun, U = mg den önemli ölçüde farklı olmasını bekleriz.
Potansiyel enerji fonksiyonunun bu genel biçimini hesaplamadan önce, çekim kuvvetinin korunumlu olduğunu doğrulayacağız. Çekim kuvvetinin korunumlu tabiatını tanıtmak için, onun bir merkezi kuvvet olduğunu hatırlayalım. Tanım olarak, bir merkezi kuvvet, sabit bir merkezden çıkan bir radyal doğru boyunca yönelmiş ve büyüklüğü yalnızca radyal koordinat r’ye bağlı olan bir kuvvettir. Buradan, r gösterildiği gibi başlangıçtan parçacığa yönelmiş bir birim vektör olmak üzere, bir merkezi kuvvet F(r) r ile temsil edilebilir.
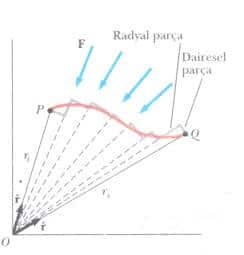
P’den Q’ya olan genel bir yol boyunca hareket eden bir parçacığın üzerine etki eden bir merkezi kuvveti düşününüz. P’den Q’ya giden yol aşağıdaki tarzda bir seri ışınsal (radyal) ve dairesel parçalarla temsil edilebilir. Kesikli çizgilerle gösterildiği gibi, belirli sayıda ince kama dilimleri çiziyoruz. Kamaların dış sınırları kısa radyal doğru parçalarıyla daire parçalarından (şekildeki gri kısımlar) meydana gelmiştir. Her bir kamanın radyal boyut uzunluğunu, kamanın geniş ucundaki kısa dairesel parçamız, parçacığın gerçek yörüngesini kesecek şekilde seçiyoruz. Bu taktirde, gerçek yörüngeyi, nöbetleşe olarak bir daire parçası ve radyal parça boyunca gidip gelen bir dizi zigzag hareketleriyle yaklaşık elde etmiş oluruz.
Tanımdan dolayı, bir merkezi kuvvet daima radyal parçalardan biri boyunca yönelmiştir; bu yüzden herhangi bir radyal parça boyunca F tarafından yapılan iş ile verilir.
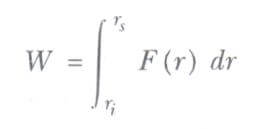
Tanım gereği, yer değiştirmeye dik bir kuvvetin yaptığı işin sıfır olduğunu hatırlayınız. Buradan, herhangi bir dairesel parça boyunca yapılan iş sıfırdır, çünkü F, bu parçalar boyunca olan yer değiştirmeye diktir. O halde, F tarafından yapılan toplam iş ışınsal (radyal) parçalar boyunca yapılan işlerin toplamıdır.
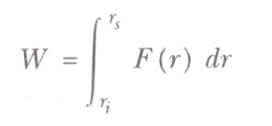
Burada i ve s alt indisleri başlangıç ve son konumu gösterir. İntegral yalnız konumun bir fonksiyonu olduğu için, bu integral’in sonucu sadece r’nin başlangıç ve son değerlerine bağlıdır. Böylece, P’den f’ye giden her yol boyunca yapılan iş aynıdır. Yapılan iş yoldan bağımsız olduğu ve yalnız uç noktalara bağlı bulunduğu için her merkezi kuvvetin korunumlu olduğu sonucuna varırız. Şimdi bir kez merkezi kuvvetin biçimi belirtildiğinde, potansiyel enerji fonksiyonunun elde edilebileceğinden emin bulunuyoruz.
Verilen bir yer değiştirmeye karşılık kütle çekim potansiyel enerjisindeki değişimin, bu yer değiştirme süresince çekim kuvvetinin yaptığı işin negatifi veya olarak tanımlandığını hatırlayız.
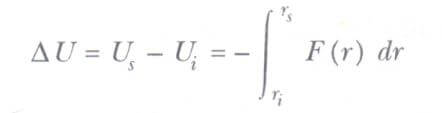
Bu sonucu, çekim potansiyel enerjisi fonksiyonunu bulmakta kullanabiliriz. Yer yüzeyinin yukarısında P ve Q noktaları arasında hareket eden m kütleli bir parçacık alalım. Parçacık, yukarıdaki formül’de verilen çekim kuvvetinin etkisi altındadır, m ’ye etki eden kuvveti aşağıdaki biçimde ifade edebiliriz.
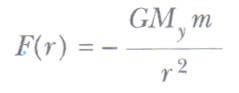
Burada eksi işareti kuvvetin çekici olduğunu gösterir. Bunu 2 üst formül’de yerine koyarak kütle çekimi potansiyel enerji fonksiyonundaki değişmeyi hesaplayabiliriz.
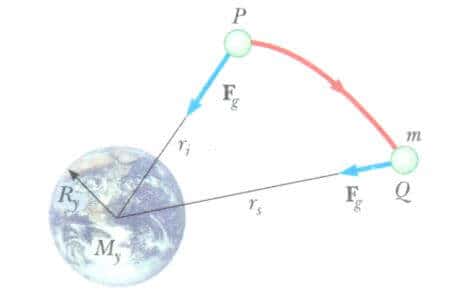
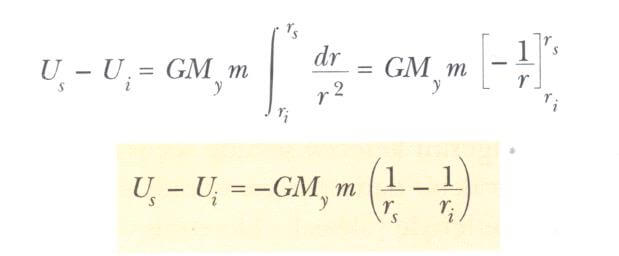

Her zaman olduğu gibi, potansiyel enerji için referans noktasının seçimi tamamen keyfidir. Referans noktasını, kuvvetin sıfır olduğu yerde seçmek adettir.
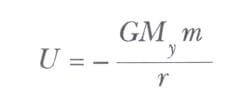
r > Ry olmak şartıyla, bu önemli sonuç r uzaklığı ile ayrılmış Dünya parçacık sistemi için geçerlidir. Bu sonuç r< Ry olan Dünya içindeki parçacıklar için geçerli değildir.
Her ne kadar hemen üstteki eşitliği parçacık Dünya sistemi için çıkartıldıysa da, herhangi iki parçacık için aynı şekilde geçerlidir. Yani, m1 ve m2 kütleli ve birbirinden r uzaklığıyla ayrılmış herhangi bir parçacık çiftine eşlik eden çekim potansiyel enerjisi aşağıdaki formül ile verilir.
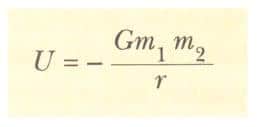
Bu ifade, herhangi bir parçacık çifti için çekim potansiyel enerjisinin 1/r şeklinde değiştiğini, öte yandan aralarındaki kuvvetin ise 1/r2 olarak değiştiğini gösterir. Bu eşitlikte, kuvvet çekici olduğu için potansiyel enerji negatiftir ve parçacıklar arası uzaklık sonsuz iken potansiyel enerji sıfır olarak alınmıştır. Parçacıklar arasındaki kuvvet çekici olduğundan, iki parçacık arasındaki uzaklığı arttırmak için bir dış etken pozitif iş yapmalıdır. İki parçacık ayrıldıkça dış etken tarafından yapılan iş potansiyel enerjide bir artış getirir. Yani, r arttıkça U daha az negatif olur.
İki parçacık durgun ve bir r uzaklığında bulunduğunda, bir dış etken parçacıkları sonsuz uzaklığa kadar ayırmak için en azından G.m1.m2/r ye eşit bir enerjiyi vermek zorunda kalır. Bu sebeple potansiyel enerjinin mutlak değerini, sistemin bağlanma enerjisi olarak düşünmek uygundur. Eğer dış etken, bağlanma enerjisi G.m1.m2/r den daha büyük bir enerji verirse, sisteme verilen fazla enerji, parçacıkların sonsuz uzaklıkta bulundukları zamanki kinetik enerjileri olacaktır.
Bu fikri üç veya daha fazla parçacığa genişletebiliriz. Bu durumda, sistemin toplam potansiyel enerjisi, bütün parçacık çiftleri üzerinden alınan toplamdır. Her bir çift, hemen üstteki eşitlik ile verilen biçimdeki bir terim kadar katkıda bulunur. Örneğin, sistem altta şekildeki gibi üç parçacık içerir ise alttaki formül ile buluruz.
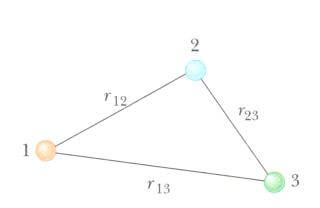
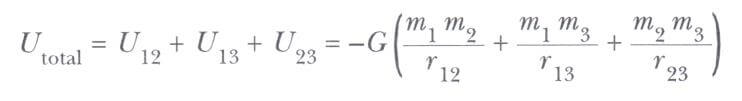
U toplam m mutlak değeri, parçacıkları sonsuz uzaklığa kadar ayırmak için gerekli olan işi temsil eder.
Bütün parçacık çiftleri için potansiyel enerji terimlerinin toplanabilmesi, kütle çekim kuvvetlerinin üst üste binme ilkesine uyması deneysel gerçeğinden kaynaklanır.


