Matematiğin önemli dallarından bir tanesi de topolojidir. Topoloji nesneleri yırtmadan kesmeden farklı farklı nesnelere dönüştürme işidir. 19 yy. temelleri atılsa da 20 yy. da bu alanda önemli çalışmalar yapılmış ve sağlam temellere oturtulmuştur. Topolojinin en kolay tarifi ise genelde matematikçiler tarafından “lastik geometri” olarak nitelendirilmektedir. Aşağıda bahsedeceğimiz problemler her tarafta bilinen problemlerdir. Bu yazıyla hem topolojiye giriş yapıp yeni nesneler yapacağız. Königsberg köprüsü problemi ile aslında topoloji başlamıştır.
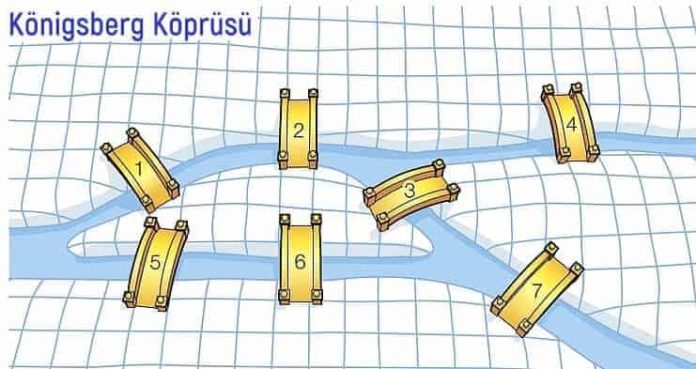
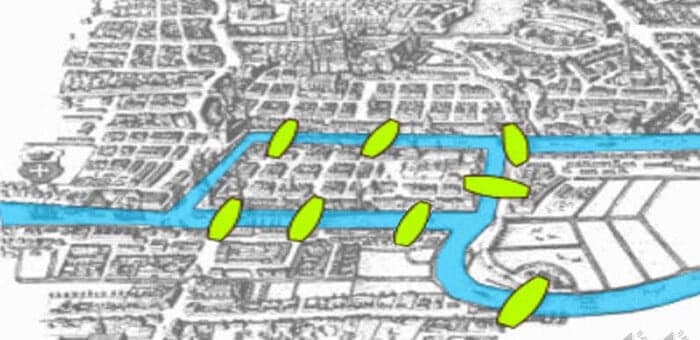
Köningsberg Eskiden Rusya’ya bağlı olmasına rağmen şimdi Almanya sınırları içerisinde bulunan bir kenttir. Fakat Königsberg bir ırmak üzerinde iki adadan oluşuyordu. Bu adalar ise birbirine yollar ile bağlıydı. Adalardan biri ırmağın iki kıyısına ikişer köprü; diğeri de birer köprü ile bağlanmıştır. Ayrıca iki adasında bir köprü vardır. Kentteki insanlar pazar günleri her köprüden yalnızca bir kez geçerek tüm köprülerden geçmeye çalışıyorlardı.
Bu gelenekselleşmiş olay Leonhard Euler’ın kulağına gider. Kimse tek seferde geçemediği için insanların kafasında hep bir merak konusu olmuştu. Euler işte bu problemin çözümüne uğraşırken aynı zamanda şimdiki Graf – Çizgeler Kuramının temelini atmıştır. Grafları kullanarak her köprüden bir kere geçmenin imkansız olduğunu gösterdi. Çözümün ardından Euler, “Solutio problematis ad geometriam situs pertinentis” isimli makaleyi yayımlamıştır.
Peki böyle bir gezinme nasıl mümkündür? Euler yazdığı makalede bu şekilde bir gezinti için graf düğümleri için bir kaç özellik vermiştir. Bunlar;
- Birleşik bir grafın bütün elemanlarını bir ve yalnız bir defa kullanarak dolaşmak için o grafın tek dereceli düğümlerinin sayısı eğer varsa iki olmalıdır.
- Tek dereceli düğümler dolaşmanın başlangıç ve bitiş düğümleridir. Grafta böyle düğümler yoksa dolaşmaya herhangi bir düğümden başlanabilir.
 Matematiksel Yaklaşımı Nasıl Yapacağız.
Matematiksel Yaklaşımı Nasıl Yapacağız.
Tanım. Birbirine bağlı eğriler veya doğrular (edges) ile noktalardan (vertices) oluşan şekle bir grafik denir.
Şimdi problem, bir çizgiden bir daha geçmeksizin ve kalemi kağıttan kaldırmaksızın bu şekli çizme problemine dönüşmüş olur.
Tanım. Eğer bir grafikte bir noktaya tek sayıda eğri bağlı ise bu noktaya tek mertebeden bir nokta denir aksi takdirde çift mertebeden nokta denir. Bu tanımları yapmazsak olmazdı.
Euler’in Königsberg köprüleri probleminin çözümünde grafiği çizerken işlemin ortasında bir noktaya gelindiğinde bu noktaya bir tane gelen bir tane de bu noktadan giden eğri olmalı böylece noktanın mertebesi çift olmalıdır. Bu bütün noktalar için doğru olmalı fakat biri çizime başladığımız diğeri de çizimi bitirdiğimiz nokta olmak üzere iki nokta dışında her noktanın mertebesi çift olmalıdır ve böylece ilgili grafiğin çizilebilir olması için gerek ve yeter koşul en fazla iki tane tek mertebeden noktasının olmasıdır. (Başlangıç ve bitiş noktasının aynı olabilir ki bu durumda her noktanın mertebesinin çift olması gerekiyor.) Şimdi yukarıdaki grafiğe baktığımızda ikiden fazla tek mertebeden nokta olduğunu görüyoruz ve böylece grafik çizilemez yani Königsberg deki yürüyüş turu imkansızdır. Burada çizimden kastımız bir çizgi ya da kenardan (veya eğri parçasından) bir daha geçmeksizin çizimin yapılması anlamındadır. Eulerin düşüncesi çözülebilir olan problemlerde başlangıç noktası tek ve bitiş noktasının tek mertebeden olması gerektiğini vermektedir.
En üsteki grafda her noktanın mertebesi yanında yazılı bulunmaktadır. Şekilde Königsberg köprüleri probleminde her bir noktanın mertebesini görmekteyiz.
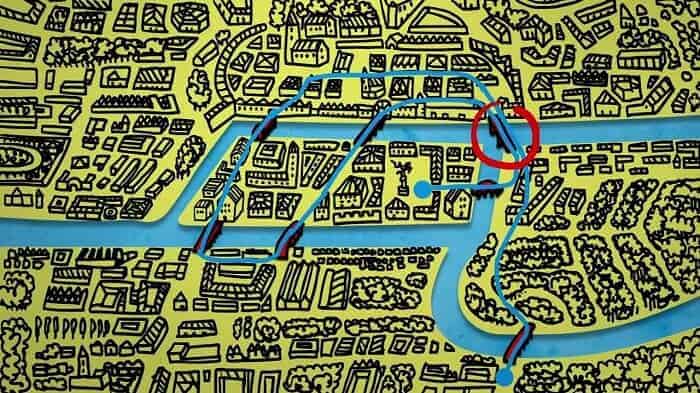
Königsberg’de aşağıdaki şekilde olduğu gibi bir tane fazla köprü yapıldığını yani sekiz tane köprü kurulduğunu varsayalım. Bu durumda bir köprüden (çizgiden) bir daha geçmeden bütün köprülerden geçilebilir mi? Evet geçilebilir.