Bir topolojik nesne olarak Möbius şeridi hakkında bize neler hissettirmesi gerektiğini öğrendik. Möbius şeridine benzer biçimde elde edilen bu şişe ise tek bir ağızdan oluşmaktadır. Yine aynı biçimde tek yüzü vardır, aslında bunun tek sebebi kapalı bir yüzey olmasındandır. Klein şişesinin bundan dolayı iç yüzeyi olmayıp sadece dış yüzeyi vardır. Yukarıda dediğimiz gibi tek ağzı olduğu, içine dökülen herhangi bir sıvı yine aynı açıklıktan dökülecektir. Yani sakın sürahi olarak kullanayım demeyin.
Möbius şeridi ve Klein şişesi için ortak hareketlerle yapıldığını söyledik. Aralarındaki fark ise Möbius şeridini üç boyutta gösterebilmemize rağmen, Klein şişesi için dört boyuta ihtiyacımız vardır.
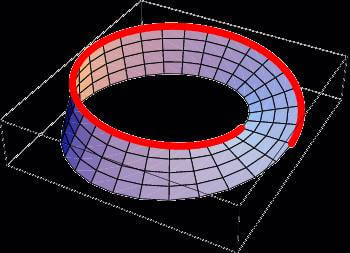Möbius Şeridini yaparken, dikdörtgen biçimindeki şeridi uçlarından 180 derece ters olacak şekilde yapıyorduk. Klein Şişesini yaparken ise bir silindiri aynı yukarıdaki biçimde 180 derece ters olacak şekilde birleştirilerek elde edilir.
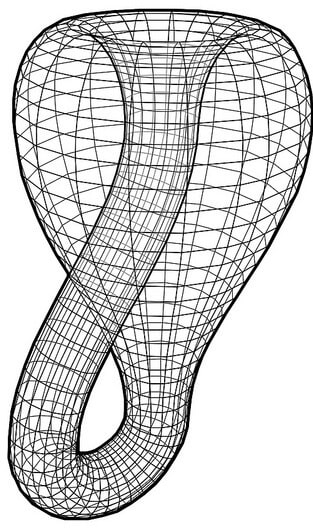Yukarıda boyutla ilgili açıklanan cümleler birçok kişi tarafından eleştirilebilir. Klein şişesine bakarken ona 4-boyutlu uzayda var olan bir varlığın 3-boyutlu uzaydaki yansıması olarak bakınız. Yani, Klein şişesi 4-boyutlu uzayda var olan bir nesnedir. Fakat üç boyutlu uzaydaki yansımasında bir kesik varmış gibi görünmektedir. Ancak, elinizle onun yüzeyini yokladığınızda kapalı ve sonlu fakat hudutsuz 2-boyutlu bir yüzey olduğu sonucuna varırsınız. İnanmayan varsa şayet, tam ortasından kestiğimizde iki adet Möbius şeridi karşımıza çıkacak. Biz bu şeridi 2 boyutta, 3.boyutun yansıması olarak olarak söylemiştik. Tek yüzü olmasına karşın (2 boyut) en, boy ve yükseklik biçiminde görülmesi olayı Klein şişesi için de geçerlidir.
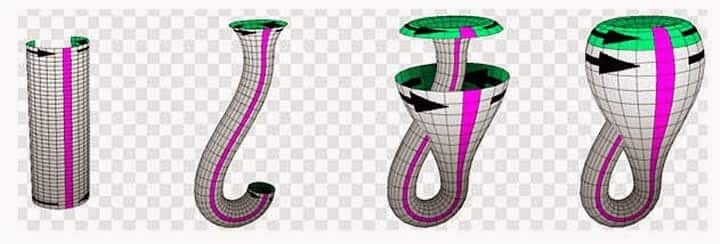Peki Klein şişesine baktığınızda kulpu varmış gibi görünüyor, değil mi? Sakın aldanmayın, bu geometrinin bize oynadığı bir oyundur bu bir yanıltıcı görüntüdür. Bu yanılgı 4-boyutlu Klein şişesini bilgisayarda programladığınızda açıkça ortaya çıkmaktadır. Görüntüde Klein şişesi hem kulplu hem de kulpsuz gözükür. (Bakmasını bilene!)