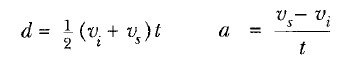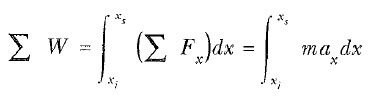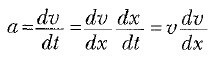Merhaba arkadaşlar bu yazımızda sizlere kinetik enerji nedir ve iş kinetik enerji teoremi konu başlıklarını anlatacağız. Karmaşık kuvvetler içeren hareket problemlerini çözmede Newton’un ikinci yasasını kullanmak zor olabilir. Başka bir yaklaşım, bir takım net kuvvetlerin etkisi altında hareket eden parçacığın süratini yer değiştirmeye bağlamaktır. Bir parçacık üzerinde net kuvvetin yaptığı iş, verilen bir yer değiştirme için hesaplanabilirse, parçacığın süratindeki değişme kolayca hesaplanabilir.
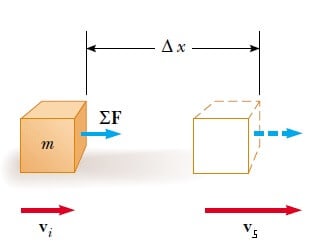
Şekil 1, sabit net bir ∑F kuvvetinin etkisi altında sağa doğru hareket eden m kütleli bir parçacığı göstermektedir. Kuvvet sabit olduğu için, Newton’un ikinci yasasına göre parçacığın sabit bir a ivmesiyle hareket edeceğini biliyoruz. Parçacık bir d uzaklığı kadar yer değiştirmişse, toplam ∑F kuvvetinin yaptığı iş
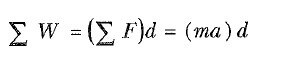
olur. Bir parçacık sabit ivme ile gittiğinde aşağıdaki bağıntıların geçerli olduğunu bilmemiz gerek;
Burada vi, t = 0 ‘daki sürat ve vs, t anındaki sürattir. Bu ifadeler. Eşitlik 1 e yerleştirilirse
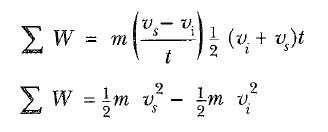
elde edilir.
1/2mv2 niceliği parçacığın hareketiyle ilgili enerjiyi temsil eder. Bu nicelik, kinetik enerji gibi özel bir isim verilecek kadar önemlidir. Bir parçacığa etkileyen net sabit bir ∑F kuvveti tarafından parçacık üzerinde yapılan iş, onun kinetik enerjisindeki değişime eşittir.
Genel olarak bir v süratiyle hareket eden m kütleli bir parçacığın K kinetik enerjisi:
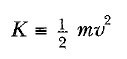
olarak tanımlanır.
İş Kinetik Enerji Teoremi
Kinetik enerji nedir; Kinetik enerji skaler bir nicelik olup, iş ile aynı birime sahiptir. Örneğin, 4 m/s’lik süratle giden 2 kg’lık bir kütlenin 16J’lük bir kinetik enerjisi vardır. Tablo 1’de çeşitli cisimlerin kinetik enerjileri verilmektedir.
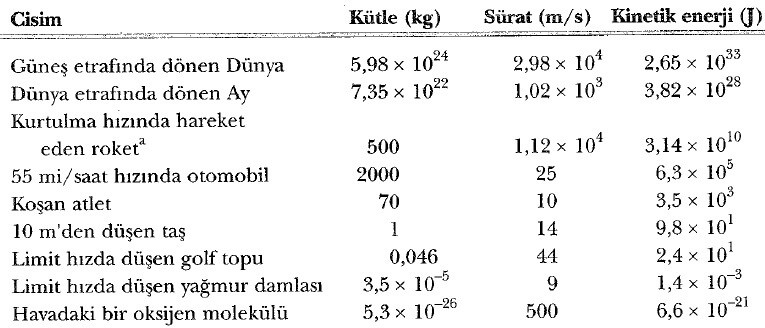
Genellikle, Eşitlik 2 ye
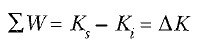
biçiminde yazmak uygun olur. Yani Ki + ∑W = Ks
Eşitlik 4, iş – kinetik enerji teoremi olarak bilinen önemli bir sonuçtur. Yapılan net işin hesabında, bu teoremi kullandığımız zaman parçacık üzerinde iş yapan tüm kuvvetleri almamız gerektiği unutulmamalıdır. Bu teoreme göre bir parçacığın üzerinde yapılan net iş pozitifse, süratinin artacağını görüyoruz. Çünkü, son kinetik enerji, ilk kinetik enerjiden daha büyüktür. Yapılan net iş negatifse, son kinetik enerji ilk kinetik enerjiden daha küçük olacağından parçacığın sürati azalır.
4 Eşitliğiyle ifade edilen iş-kinetik enerji teoriminde kinetik enerji bir parçacığın durgun hale gelmesi sonucu yapabileceği iş veya parçacıkta depo edilen enerji miktarı olarak düşünülebilir. Örneğin bir çekicin bir çiviye çarpmak üzere olduğunu varsayınız. Hareketli çekiç kinetik enerjiye sahiptir ve çivi üzerinde iş yapabilir. Çivi üzerinde yapılan iş, Fd ‘ye eşittir. Burada F, çekicin çiviye uyguladığı ortalama kuvvet ve d çivinin duvara girdiği uzaklıktır.
İş-kinetik enerji teoremini sabit bir net kuvvet varsayımı ile türettik, fakat sonuç kuvvet değişken olduğunda da geçerlidir. Bunu görmek için bir parçacık üzerine x yönünde etkiyen net kuvvetin X Fx olduğunu varsayınız. YJ’X -max şeklindeki Newton’tın ikinci yasasını kullanarak yapılan net işi
olarak ifade edebiliriz. Bileşke kuvvet x ile değişirse ivme ve hız da x’e bağlı olur. İvmenin normalde t nin bir fonksiyonu olduğunu düşündüğümüzden şimdi biraz farklı yolla a yı ifade etmek için aşağıdaki zincir kuralını uyguluyoruz:
a ‘nın bu ifadesini ∑W ‘de yerine koyarsak;
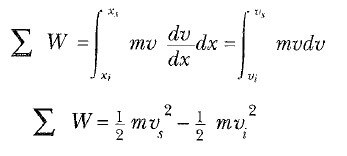
eşitliğini buluruz. Değişken x den v ye değiştiği için, integralin sınırları x değerlerinden v değerlerine değiştirildi. Buna göre, bir parçacığa etkileyen net kuvvetin, parçacık üzerinde yaptığı net işin, parçacığın kinetik enerjisindeki değişime eşit olduğu sonucunu çıkarıyoruz. Net kuvvet sabit olsa da olmasa da bu söz doğrudur.