Gezegenlerin, yıldızların, ve gökyüzündeki diğer cisimlerin hareketleri binlerce yıl insanlar tarafından gözlenmiştir. Tarihte ilk zamanlar bilim adamları, Dünyayı Evren’in merkezi gibi saydılar. Yer merkezli model de denilen bu model, Yunan astronomu Claudius Ptolemy (MS 100-170 yılları) tarafından Milattan sonra ikinci yüzyılda biçimlendirilmişti ve takip eden 1400 yıl boyunca kabul gördü. 1543 yılında Polonyalı astronom Nicolaus Copernicus (1473-1543) Dünyanın ve diğer gezegenlerin Güneş etrafında dairesel yörüngelerde dolandıklarını teklif etti (güneş merkezli hipotez).
Danimarkalı astronom Tycho Brahe (1546-1601), gökyüzünün nasıl kurulduğunu belirlemek istedi. Bu amaçla yıldızların ve gezegenlerin konumlarını belirlemek için bir program geliştirdi. Gezegenler ve çıplak gözle görülebilen 777 yıldız üzerinde yapılan bu hassas gözlemlerin, (henüz teleskop icat edilmediğinden), büyük bir yükseklik ölçer ve pusulayla yapıldığı dikkat çekicidir.
Brahe’nin asistanlığını yapan Alman astronom Johannes Kepler, hocasının astronomik verilerini kullanarak gezegenlerin hareketlerine ait bir matematiksel model çıkartmak için 16 yıl uğraştı. Dünya da Güneş’in etrafında hareket ettiği için bu tür verilerin düzenlenmesi zordur. Yorucu birçok hesaplamalardan sonra, Brahe’nin, Mars’ın güneş etrafındaki dönmesine ait bulduğu hassas verilerin cevabı sağladığını gördü. Kepler ilk önce, güneş etrafındaki dairesel yörüngeler fikrinin bırakılması gerektiğini gösterdi. Sonunda, Mars’ın yörüngesinin, bir doğru bir şekilde tarif edilebileceğini keşfetti.
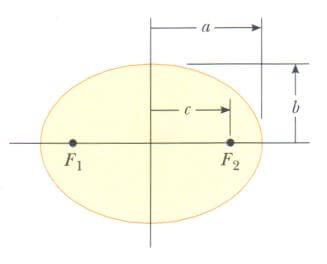
Şekildeki gibi bir elipsin geometrik tanımını vermektedir. En büyük boyutuna büyük eksen denir ve uzunluğu 2a’dır. a’ya da büyük yarı eksen denir. En küçük boyutu küçük eksendir, 2b uzunluğunda olup b’ye de küçük yan eksen denir. Ayrıca, elips merkezinden c uzaklığında odak noktası vardır, a^2 = b^2 + c^2 dir. Güneş, Mars yörüngesinin odaklarından birine yerleşmiştir. Daha sonra bu fikri bütün gezegenlerin hareketlerini kapsayacak şekilde genelleştirdi. Bunlar, Kepler yasaları diye bilinen, üç ifadede özetlenir:
Kepler Yasası
- Bütün gezegenler, odak noktalarından birinde güneş bulunan eliptik yörüngelerde dolanırlar.
- Güneşten herhangi bir gezegene çizilen yarıçap vektörü, eşit zaman aralıklarında eşit alanlar süpürür.
- Herhangi bir gezegenin yörünge periyotunun karesi, eliptik yörüngesinin büyük ekseninin yarısının küpüyle orantılıdır.
Gezegen yörüngelerinin çoğunun şekli daireye yakındır; örneğin, Mars’ın yörüngesinin büyük eksenin yarısı ile küçük eksenin yarısı yalnızca % 0,4 farklıdır. Merkür ve Plüton, dokuz gezegenden en eliptik yörüngeli olanlardır. Gezegenlere ilave olarak, Güneş’in etrafında dolanan ve Kepler yasalarına uyan daha bir çok küçük yıldızlar ve kuyruklu yıldızlar vardır. Halley kuyruklu yıldızı böyle bir cisimdir. Güneş’e yakın olduğunda her 76 senede bir kez görülebilir hale gelir. Yörüngesi çok eliptiktir ve küçük yarı ekseni, büyük yarı ekseninden % 76 daha küçüktür.
Her ne kadar burada ispat etmese de, Kepler’in birinci yasası, kütle-çekim kuvvetinin 1/r2 olarak değişmesinin doğrudan bir sonucudur. Yani, bir ters kare kütle çekim kuvveti altında, gezegenin yörüngesinin odak noktalarından birinde Güneş’in bulunduğu bir elips olacağı matematiksel olarak gösterilebilir.
Gerçekten Kepler’in bu yasaları bulmasından yarım asır sonra, Newton bu yasaların herhangi iki kütle arasında var olan kütle çekim kuvvetinin bir sonucu olduğunu gösterdi. Newton’un evrensel çekim yasası ve geliştirdiği hareket yasaları, gezegenlerin ve uyduların hareketinin tam bir matematiksel çözümünün temelini oluşturur.
Evrensel Çekim Kuvveti ve Gezegenlerin Hareketi
Newton, kendi evrensel çekim yasasını formüle ederken çekim kuvvetinin, uzaklığın karesinin tersiyle orantılı olduğunu telkin eden şu akıl yürütmeyi kullandı. Ay’ın merkezcil ivmesini, Dünyanın yüzeyine yakın bir yerden düşmekte olan hikayesi anlatılan elma gibi bir cismin ivmesiyle karşılaştıralım. Her iki ivmenin sebebinin aynı olduğunu, yani Dünya’nın kütle çekiminden kaynaklandığını kabul edelim. Ters kare yasasından Newton, Ay’ın Dünya’ya doğru olan ivmesinin (merkezcil ivme) 1 /rAy^2 ile orantılı olması gerektiğini buldu, burada rAy Dünya ile Ay’ın merkezleri arasındaki uzaklıktır. Bundan başka, Ry Dünyanın yarıçapı veya Dünya ile elmanın merkezleri arasındaki uzaklık olmak üzere, elmanın dünyaya doğru ivmesi 1 /Ry^2 ile orantılı olarak değişir. rAy = 3,84 х 10^8 m ve Ry = 6,37 x 10^6 m değerlerini kullanarak Ay’ın aAy ivmesinin, elmanın g ivmesine oranını aşağıdaki gibi tahmin etti.
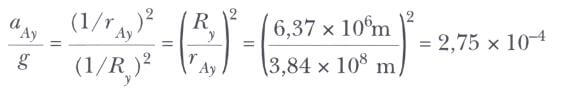
O halde Ayın merkezcil ivmesi:
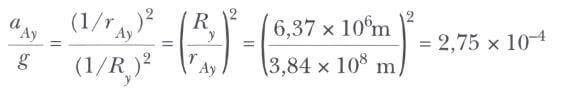
Newton aynı zamanda Ayın merkezcil ivmesini, yörüngesel periyodu T = 27,32 gün = 2,36 x 10^6 s ve Dünya’ya olan ortalama uzaklığını kullanarak kinematik olarak ta hesapladı. Bir T zamanı içinde Ay 2πrAy uzaklığı kadar yol alır, bu onun yörüngesinin çevresidir. Bu sebeple, ayın yörüngesel hızı 2πrAy/ T ve merkezcil ivmesi aşağıdaki gibidir.
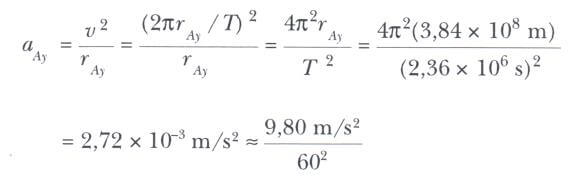
Başka bir deyişle, Ay kabaca 60 Dünya yarıçapı kadar uzakta olduğundan bu uzaklıktaki kütle-çekim ivmesi, Dünyanın yüzeyinde’kinin yaklaşık 1/60^2 kadarı olmalıdır. Bu da tam olarak Ayın dünya çevresindeki dairesel hareketi için gerekli olan ivme kadardır. Bu değerle Newton’un g’yi kullanarak elde ettiği değer arasındaki mükemmele yakın bu uyuşma, ters-kare kuvvet yasasının doğruluğu hakkında kuvvetli delil sağlar.
Bu sonuçlar, Newton için çok teşvik ediciyse de, çözümleme sırasında yaptığı bir kabulden dolayı derin rahatsızlık duyuyordu. Dünya yüzeyinde bulunan bir cismin ivmesini hesaplamak için, Dünya’yı sanki bütün kütlesi merkezinde toplanmış gibi işleme sokmuştu. Yani Newton, Dünya’yı, kendi dışında bulunan bir cismin üzerine etkisi bakımından noktasal bir kütle gibi kabul etmişti. Birkaç yıl sonra, 1687’de Newton bu kabulün geçerli olduğunu ve evrensel kütle çekimi yasasının doğal bir sonucu olduğunu, matematik analizin gelişmesine öncülük eden eserinde ispat etti.
Kepler’in Üçüncü Yasası
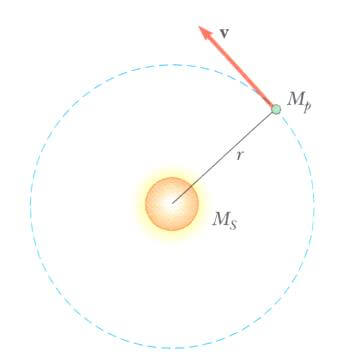
Keplerin üçüncü yasasının, dairesel yörüngelere ait ters-kare yasasından çıkabileceğini göstermek aydınlatıcıdır. Kütlesi Ms olan güneşin etrafında dairesel bir yörüngede Şekil’deki gibi hareket eden Mp kütleli bir gezegen alalım. Gezegenin üzerine Güneş tarafından uygulanan kütle çekim kuvveti, gezegenin hareketini sağlayan yarıçap boyunca yönelmiş bir kuvvet olduğundan, gezegene Newton’un ikinci yasasını (∑F = ma) uygulayabiliriz.
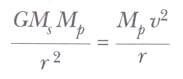
Fakat, T gezegenin dönme periyodu olmak üzere, gezegenin yörüngesel hızı basitçe 2πr/ T’dir, bu yüzden yukarıdaki ifade aşağıdaki hale getirilir.
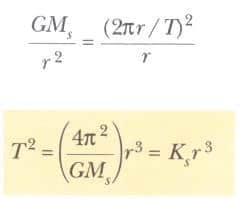
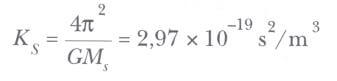
Yukarıdaki eşitlikler, Kepler’in üçüncü yasasıdır. Eğer r ’yi elipsin büyük ekseninin yarısı olan a ile değiştirirsek, yasanın eliptik yörüngeler için de geçerli olduğu gösterilebilir. Orantı sabiti Ks, gezegenin kütlesinden bağımsızdır. Bu yüzden eşitliği herhangi bir gezegen için de geçerlidir.
Dünya çevresindeki bir uydunun yörüngesini dikkate alırsak, örneğin Ay gibi, o zaman, Güneş’in kütlesi Dünya’nın kütlesiyle değiştirileceğinden, sabit, farklı bir değer alacak ve bu durumda orantı sabiti olacaktır.
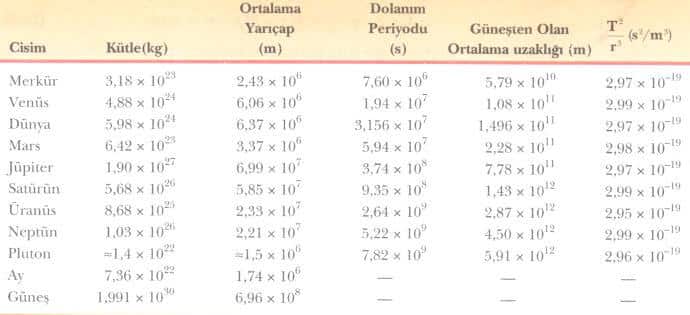
Kepler’in İkinci Yasası ve Açısal Momentumun Korunumu
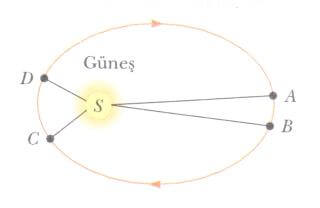
Güneşin çevresinde eliptik bir yörüngede hareket eden m kütleli bir gezegen alalım. Gezegenin üzerine etki eden çekim kuvveti daima yarıçap vektörü boyuncadır ve güneşe doğru yönelmiştir (Şekil a). Sabit bir noktaya veya ondan uzağa doğru yönelmiş, sadece r’nin fonksiyonu olan bir kuvvet merkezi kuvvet adını alır. Bu merkezi kuvvetten dolayı gezegenin üzerine etkiyen döndürme momenti (tork), F kuvveti r ’ye paralel olduğundan açıkça sıfırdır.
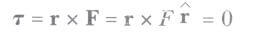
Bir gezegenin üzerine Güneş tarafından uygulanan kütle-çekimi kuvveti, gezegen üzerinde hiç bir döndürme momenti (Tork) oluşturmaz ve gezegenin L açısal momentumu sabittir.
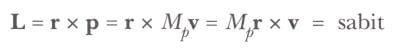
L bir hareket sabiti olduğu için, gezegenin herhangi bir andaki hareketi; r ve v tarafından oluşturulan düzlem üzerindedir.
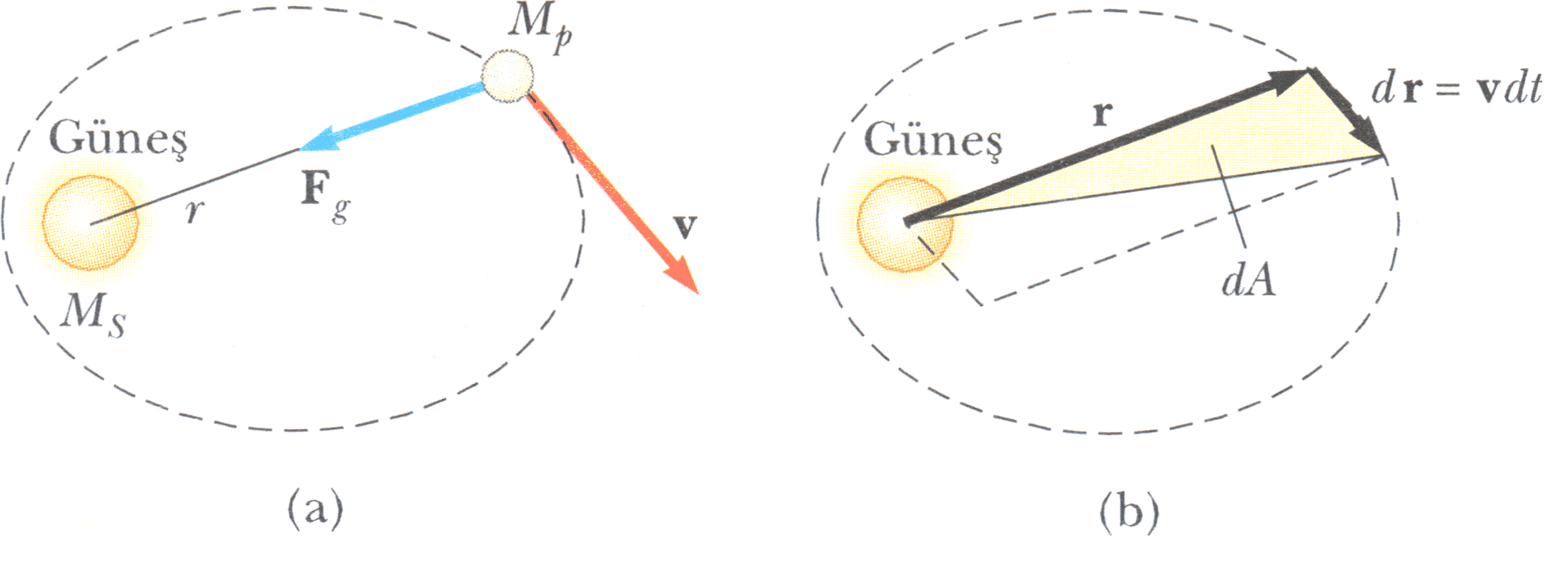
Bu sonucu şu geometrik düşünceyle anlatabiliriz. Şekil b’deki r yarıçap vektörü, bir dt zamanında dA alanını süpürür. Bu alan r ve dr vektörlerinin oluşturduğu paralel kenarın | r x dr | alanının yarısına eşittir. Gezegenin bir dt zamanındaki yer değiştirmesi dr = v dt ile verildiğinden aşağıdaki durumu elde ederiz.
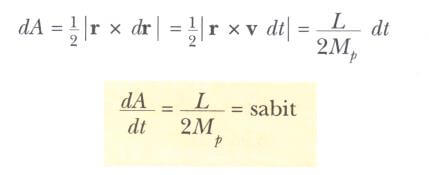
Burada L ve Mp nin her ikisi de sabittir.
Böylece:
“Güneş’ten herhangi bir gezegene uzanan yarıçap vektörü, eşit zamanlarda eşit alanlar süpürür.”
sonucuna varırız. Kepler’in ikinci yasası olan bu sonucun, çekim kuvvetinin bir merkezi kuvvet oluşundan kaynaklandığı ve onun da dolaylı olarak açısal momentumun korunumunu ifade ettiğini kavramak önemlidir. Bundan dolayı Kepler’in ikinci yasası, ister ters kare olsun isterse olmasın bir merkezi kuvvet ihtiva eden herhangi bir durum için geçerlidir.


