Kaos Teorisi’nin Ölçme ve Metroloji’ye Etkileri

Kaos ilk başlarda Çin Mitolojisi’nin ve Yunan Mitolojisi’nin yaradılış efsanelerinde kullanılmıştır. Çin Mitolojisi’nde, Kaos’tan (kargaşa) düzene (kozmos) geçişten bahsedilmiştir. Yunan Mitolojisi’nde yine aynı şekilde Kaos ve kozmos birbirinin zıttı olarak yer almıştır. Latince kökenli olan bu kelime “chaos” olarak kullanılmaktadır. İngilizcede de doğrudan bu şekilde kullanılmaktadır. Türkçe ’ye “kaos” olarak kazandırılan bu kelime “kargaşa”, “karmaşıklık”, “keşmekeş” anlamlarını karşılamaktadır.

Her ne kadar milattan önceki süreçte Yunan ve Çin mitolojilerinde Kaos’a benzer şekilde yaradılış efsaneleri yer almış olsa da; Kaos’la ilgili elle tutulur ilk veri 1889 tarihinde Astronomi ile alakalı olarak sorulan “üç cisim problemi’’ ile ortaya çıkmıştır. Güneş siteminin gerçekten kararlı olup olmadığına ilişkin merakı gidermek adına ortaya atılan bu soruya Norveç Kralı’nın ödül koymasıyla ilgi ve alaka artmıştır. Karaçay’a göre Henri Poincaré güneş sisteminin çözümünün başlangıç koşullarına hassas bağımlı olduğunu ve haliyle evrenin başlangıç koşullarını bilemeyeceğimizden güneş sisteminin de kararlı olup olmadığının asla öngörülemeyeceğini ispatlamıştır ve teknik anlamda ilk defa “Kaos” terimini kullanmıştır [1]. Problemi Poincaré çözememiştir; fakat çözülemeyeceğini ispatlamış olması da ödülü elde etmesine yetmiştir.

Ele alınan cisim sayısı iki veya daha çok olduğunda sistemin başına neler geleceğini tahmin etmek imkânsız bir hal almaktaydı. Yani ikiden çok daha fazla cismi içinde barındıran güneş sisteminin ileride başına neler geleceğini bulmak imkansız bir durum olarak nitelendirilebilir. Bu durum bir basit örnekle ele alınabilir. Bir kabın içinde düzensizce çarpışan gaz molekülleri ele alınırsa ve bu gaz moleküllerinin başlangıç noktası bilinirse ayrıca çarpıştıkları açıyı, çarpıştıkları hızı, … gibi sayısız değişkenle beraber ortamı etkileyen faktörleri de ele alarak bir işlem yapılırsa gaz moleküllerinin bir sonraki adımı tamamıyla kestirilebilir fakat burada önemli olan nokta başlangıç koşullarına hassas bağlılıktır ve başlangıç noktasının kestirilebilmesi mümkün değildir bununla beraber sistem içindeki değişkenlerin sayısı o kadar fazladır ki bunun hesabını tutabilecek bir program yahut bilgisayar mevcut değildir. Yeniden konuya dönülecek olunursa 1889 yılından sonra Kaos fikri akıllardan silindi ve gerçek manada Kaos tekrar Edward Lorenz’le beraber ele alındı David Ruelle Kitabında “Massachusetts Teknoloji Enstitüsü’nde meteoroloji uzmanı olan Edward Lorenz atmosferik konveksiyon olgusuna ilişkin bazı araştırmalar yapmıştır.(…) Lorenz’in zaman içindeki evrime ilişkin teorisi atmosferik konveksiyonun gerçekçi bir tanımlaması olmamakla birlikte atmosferin hareketlerinin önceden bilinmezliğe ilişkin görüşlere büyük ölçüde destek sağlamıştır. Bir meteoroloji uzmanı olarak bu bilim dalının uzun dönemli güvenilir tahminler yapamayışına bu yoldan geçerli bir neden bulmuştur. Henri Poincaré de aynı şeyleri söylemişti.” [2] yazmıştır.

Edward Lorenz’in çalışmalarından bahsedilmişti. Edward Lorenz’in çalışmalarını daha derinden incelemek; Kaos teorisinin nasıl gelişim gösterdiğini anlamak adına daha faydalı olacaktır.

Edward Lorenz havanın ısı değişimini belirlemek adına üç adet diferansiyel denklem yaratmıştır ve bu denklemde zaman değişkenine belli değerler vererek bir hava tahmin modeli oluşturmaya çalışmıştır. Denklemin oluşturduğu grafik o kadar farklı haldedir ki denkleme yeni değerler verilip grafik üç boyutlu uzayda (x,y,z) çizildikçe Edward Lorenz grafiğin sarmallaştığını ve hiçbir zaman birbirini kesmediğini görmüştür.

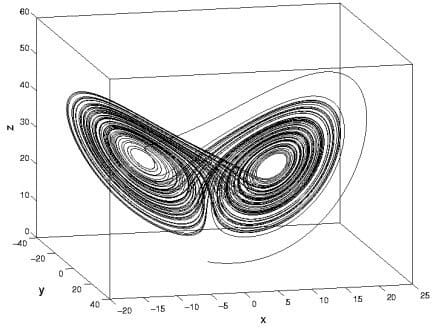
Edward Lorenz’in tekrardan gündeme getirdiği Kaos “çeker” diye nitelendirilen olguyu meydana getirmiştir. Çeker dinamik bir sistemin içinde bir yörüngenin hesaplanmasıyla, belli bir dönem yahut daima üzerinde hareket ettiği kümedir. Lorenz’in oluşturduğu hava tahmin modeli Lorenz Çekeri’ni meydana getirmiştir ve birçok bilim adamının dikkatini tekrar Kaos’a yöneltmeyi başarmıştır akabinde buna benzer birçok çeker meydana getirilmiştir (bkz. Julia ve Mandelbrot kümeleri). Matematik başta olmak üzere birçok bilim Kaos’tan yeni şeyler kazanmıştır. Çekerler tekrarlama(iterasyon) yöntemiyle meydana gelmektedir. Bu tekrarlamalarsa fraktalları meydana getirmektedir. Tekrar Lorenz Çekeri’ne dönülecek olunursa o meşhur metaforu anmadan geçmek Edward Lorenz’e saygısızlık olacaktır. Lorenz çekeri için denkleme verilecek sayılarda yapılacak ufak bir değişiklik iterasyonu tamamıyla farklı bir yöne sürükleyecektir ve oluşan grafik bambaşka olabilecektir. İşte bu olguya Kelebek Etkisi (başlangıç koşullarına hassas bağlılık) denmektedir. Yani Pekin’de kanat çırpan bir kelebek Washington’da kasırgaya sebep olabilmektedir. Çekerlerin oluşturduğu iterasyonlar Matematik biliminde yeni bir çığır açmıştır ve fraktallar konusu oluşum göstermiştir. Doğada tam manasıyla bir üçgen bile bulamazken fraktal yapılar maddeleri matematiksel olarak tanımlamamızda büyük rol oynamıştır. Bir kar tanesi büyütülerek incelendiğinde fraktallaşmayı görmek mümkündür ve hiçbir kar tanesi bilindiği üzere birbirinin aynısı değildir. Bu durumu da Kelebek Etkisi’yle açıklamak mümkündür şöyle ki; başlangıç koşullarında o kadar mikro düzeyde değişim meydana gelmektedir ki kar tanesini oluşturan fraktalların iterasyonları her birini farklı kılmaktadır. Durumlar bu derece karmaşıkken çalışmanın amacını açıklamak ve adım adım kaosu daha derinden irdelemek isabet olacaktır. Bu çalışmada Kaos Teorisinin mesafe ölçümü kapsamında “ölçme ve metroloji” üzerine etkisini spesifik olarak inceleyerek Kaos Teorisinin ne olduğuna ölçme ve metrolojinin ne olduğuna ayrıca nasıl olur da kaos teorisi ölçme ve metrolojiyi etkisi altına alır saptanacaktır. Bunlar saptanırken kaynak taraması yaparak bilgileri belli kaynaklara dayandırmak ve karmaşıklığından dolayı aşama aşama yapmak bu makaleyi oluşturan metod olacaktır.

Kaos Teorisi ve Kelebek Etkisi

Herhangi bir sistemde oluşturulan etkiye binaen vukuu bulabilecek tepkilerin belirsizlikleri ile ölçümlerin belirsizlikleri (net ölçümlerinin ve doğru tahminlerinin kestirilememesi), Kaos diye adlandırılabilir. Bu bağlamda “Kaos Teorisi’nin”, Fizik Bilimi’nde “belirsizlik” adıyla oluştuğu ve ilerlediği, sonrasında ise çoğu bilimde “Kaos” olarak ön plana çıktığı belirtilebilinir.

Karaçay’a göre doğrusal olmayan hareket sistemlerinin çoğu için öngörü yapmaya engel olan üç neden vardır: Birincisi bu sistemin analitik çözümü yoktur. İkincisi herhangi bir başlangıç koşulunu kesinlikle belirleyemeyiz. Üçüncüsü başlangıç koşullarında meydana gelen çok küçük değişim(ler) sonuçta çok büyük farklara neden olabilir [3]. Buna bağlı olarak “sistemlerin başlangıç noktası” ile ilgili verilerin elde edilememesi, analitik anlamda çözümlerinin olmaması ve nasıl meydana geldiğiyle alakalı bir formülün ortaya konulamamış olması, ayrıca sistemin devam etme sürecinin belirsizliği ortaya çıkardığı görüşü savunulabilir. Başlangıç koşullarındaki çok ufak farklılıkların bile sonuçta büyük değişimlere sebep olabilme ihtimali Kaos’un temel ilgi alanı olup Kelebek Etkisi diye adlandırılmaktadır.

Kelebek etkisi “başlangıç koşullarına hassas bağlılık” olarak tanımlanabilir. Ertürk’e göre bu örnek Edward Lorenz tarafından yapılandırılmıştır ve Lorenz bu örneği “Pekin’de kanat çırpan bir kelebeğin havada oluşturduğu hava dalgalarının gelecek ay New York’ta fırtınaya neden olabileceği” şeklinde ifade eder [4]. Çobanoğlu’na göre, sistemleri kararlı halden uzaklaştıran faktör kelebek etkisi faktörüdür. Kelebeğin kanat çırpması gibi birçok küçük değişiklik artarak devam etmesi durumunda sistemleri statik durumundan çıkarır. Bu durum olumlu ya da olumsuz yönde sistemlerde sürükleyici etki yapar [5].

Kaos Teorisi’nin ilgilendiği diğer bir problem ise Kaos’un düzenidir. Gleick’e göre Kaos teorisinde, tüm karmaşık, düzensiz ve formüle edilemeyen veriler içinde güzel, düzenli ve sağlam bir yapı vardır [6]. Bu yapıları fraktallar olarak adlandırmak mümkündür. Düzensizliğin oluşturduğu karmaşa ortaya bir resim çıkarmaktadır ve bu resim iterasyonlardan ibarettir. Her bir tekrar oluşan karmaşayı anlamlandırmakta ve iterasyonların devamında oluşan fraktal geometrisi bize doğadan herhangi bir cismin manzarasını çağrıştırabilmektedir. Bir örnek vermek gerekirse, Koch’un “kar tanesi fraktalı” örnek verilebilir. Doğada birebir karşılaşabilinecek kar tanesini, denklem oluşturup fraktala dönüştürerek gözlemlenebilmesi mümkündür. Geometrik cisimlerin neredeyse hiçbirinin doğada bire bir bulunması mümkün değilken; fraktallarla bunun çözülmesi mümkündür. Doğada hangi dağın; bir düzlemsel üçgen veya küresel üçgen şartlarını sağlayan üçgen olduğu, hangi taşın birebir kare olduğu gözlemlenmiştir? Gözlemlenmesi pek olası görünmemektedir. Doğadaki düzeni tanımlanabilmesinin tek yolu fraktallardan geçmektedir ve bu konuya dair tek örnek kar tanesiyle sınırlı değildir. Birçok örnek mevcuttur. Başka bir örnek vermek gerekirse doğada bulunan bir ağacın dallarını fraktallarla göstermek mümkündür. Bir düz çizgiyle başlanılan, çizginin üst ucuna arası 300 olacak şekilde ilk çizginin yarısı uzunluğunda iki çizgi çizilecek olunursa ve bu adımlar tekrar ettirilirse ortaya aşağıdaki görüntü çıkacaktır. Sonbaharda yapraklarını dökmüş herhangi bir ağacın bu fraktalla birebir örtüşmesi imkânsız bir olay değildir.

Ölçme ve Metroloji

İnsan var olduğu andan itibaren sürekli insanoğlu olarak bir şeyleri merak etmiş ve daima birbiriyle iletişim halinde olmuştur. Bu iletişim zamanla diğer insanlarla ilişkiye dönüşmüş ve ticari boyutlara da varmıştır. Yapılan ticaretlerde ve diğer ilişkilerde uzunluk ölçümlerine ihtiyaç duyulmuş ve bu ihtiyacı genellikle kendi vücut uzuvlarını kullanarak belirlemişlerdir. Kol, ayak, parmak gibi uzuvların her birini uzunlukla ilişkilendirip ölçüm konusunu bu uzuvları kullanarak halletmişlerdir. Her milletin yapısal farklılıklar gösterdiği dünyada özellikle uluslararası ilişkilerin de başlamasıyla, ölçümde yapılan farklılıklar sorun haline gelmeye başlamıştır. Ticaretin, bilimin ve uluslararası ilişkilerin gelişmesiyle beraber bu sorunun belli bir sisteme kavuşturulup her yerde aynı ölçümün yapılabilmesi ve haksızlıkların önüne geçilmesi ihtiyacı hissedilmiştir. Daha öncesinde basit aletlerle ölçüm yapılıyor olsa da herkesin kabul ettiği ve metrolojinin bir bilim haline gelerek, tek sistemin oturtulması ancak18. Yüzyılın sonlarına doğru mümkün olmuştur. 1700’lü yılların ortalarına gelindiğinde öncelikle Fransa’da politikacılar ve bilim adamlarının bu konudaki çalışmaları hızlanmış, doğal görüngüleri temel alan bir birim sisteminin oluşturulması için girişimler başlatılmıştır [7].

Yapılan ölçümlerde bir çeyrek meridyen uzunluğunun 10 milyonda biri “1 metre” olarak kabul edilmiştir fakat o zaman ölçüm yapılan Borda’nın tekrarlayan dairesi (repeating circle) aletinin hassaslığı ve yapılan ölçümün doğruluğu bilim adamlarını düşündürmüş ve daha geçerli bir durumu 1 metre olarak tanımlamak kararını vermişlerdir. Metre Konvansiyonu olarak adlandırılan antlaşma 17 ülke ile arasında imzalanmış ve kabul görmüştür.

İlk defa 1889 senesinde bir araya gelen Uluslararası Tartılar ve Ölçüler Konferansı hassasiyetin artmış olması ve teknolojinin de imkân verdiği düzeyde doğruluğa sahip olması, aranan doğruluk ihtiyacını karşılayacak bir metre ölçütü belirlemiştir. 1960 yılında toplanmalarının 11.cisinde astronomik ve atmosferik etkilerden dönemin imkân verdiği ölçütte uzak olarak yapılan ölçüme binaen, getirilmiş tanımlama şöyledir: “1 metre, boşluktaki (vakum altında) Kripton 86 atomundan yayılan turuncu ışınımın dalga boyunun 1650763,73 katı” [8].

Aradan zamanın geçmesiyle yapılan diğer bir konferansta metrenin tanımı şu şekilde yenilenmiştir. “Boşluktaki (vakum altında) ışığın; saniyenin 1/299 792 458’i kadar sürede kat ettiği mesafenin uzunluğu” [9] ve halen günümüzde metre olarak bildiğimiz şey bu tanımlamayla açıklanmaktadır ayrıca bu açıklama yapılan en güncel açıklamadır.

Metroloji esasında ölçüm bilimi olarak tanımlanabilir. Bu bilim dalının çalışma konusunun ölçüm olmasından kaynaklı olarak bu şekilde tanımlanması mümkündür. Yapılan en temel ölçümün de mesafe olmasından dolayı bu bilimin ilgilendiği en temel birim metredir. Bundan farklı olarak birkaç farklı birimle daha ilgilenir ve bu temel birimlerin bileşimiyle oluşan “türetilmiş birimler” i inceler. Örnek olarak yerçekimi ivmesi “g=9,80665 metre bölü saniyenin karesi”. Burada temel birimler metre ve saniyedir. Metrolojinin kelime kökü metredir. Adı üstünde deyimiyle açıklanabilecek bu bilimin temel konusunun metre olmasından dolayı ve bu çalışmada irdelenen konunun mesafeye dayanmasından dolayı metrenin incelenmesi bu çalışma adına daha yararlı olacaktır.

Metrolojinin ilerlemesiyle beraber nitekim ölçme de bu durumdan kendine düşen payı almış ve daha hassas ölçümler yapmak mümkün olmuştur. Bununla beraber yapılan ölçümlerin hassasiyeti arttıkça sonuçlar da ciddi boyutta doğruya yaklaşmıştır. Ölçmeye kısaca değinilecek olunursa “aranan bir büyüklüğün tercih edilen ölçme biriminin katları cinsinden bulunması” diye tanımlanabilir. Dünyada bir kenar yahut bir açı defalarca ölçüldüğünde bulunan her değer arasında küçük farklılıklar olduğu görülür. Yapılan her ölçümün sonucunu bire bir aynı bulmak imkânsız bir şeydir. Ölçme hataları diye adlandırılan bu farklar ölçü aletlerinin iyi kalibre edilememesinden, ölçüm yapan kişinin becerisinden ve çevresel şartların değişkenliğinden kaynaklanabilir. Hâlbuki haritaların yapılma amacına göre gereken hassasiyeti sağlaması gerekir. Bu bağlamda belirli hataların çıkarılması belirli hatalarınsa ölçüme etkisinin az olması için elimine edilmesi gerekir. Yani ölçme işleminde ortaya çıkan hataların iyi anlaşılması ve derinden incelenmesi azami derecede önem arz etmektedir.

Ölçmede Hata ve Sebepleri

Ölçmede yukarda kaynakları belirtilen hataların çeşitleri mevcuttur ve bu hataları sınıflandırarak üzerinde işlem yapılır. Genellikle dikkatsizlikten doğan, ölçüm iterasyonunda kendini bariz belli eden hatalara “kaba hatalar” denir. Çözüm olarak o ölçümün yerine daha dikkatli bir ölçüm yaparak veriyi yenilemek suretiyle veya direk o veriyi işleme sokmadan hesap yapmak usulüyle kaba hatadan kurtulmak mümkündür.

Diğer bir hata çeşidiyse “sistematik(düzenli) hatalar”dır. Bu hatalar ölçüyü aynı yönde ve aynı miktarda etkileyen hatadır. Ölçüme ne kadar etki ederse etsin hata aynı kalır ve her ölçmede o hata elde edilen verilere yapışık olarak bulunur.

Sistematik hatalardaki bu durum fraktal yapılara benzetilebilir. Bilindiği üzere fraktal yapılarda verilen oranda ve miktarda tekrar etmek suretiyle bir yapı oluşur, keza ölçmede de bu durum geçerlidir. Hata değeri, verilen orana; doğru sonuca varmak için yapılan tekrarlarsa, fraktaldaki iterasyonlara çok benzerdir. Fraktallarda ne kadar iterasyon meydana gelirse o kadar da dallanma gerçekleşir. Ölçmede ise aynı durum sistematik hatalar için bu dallanmalardan farksızdır. Bu hata türünün üstesinden gelmek adına yapılan işlemlerde mevcuttur.

Diğer bir türse “düzensiz (rastlantısal) hatalar”dır. Hemen hemen yazılmış bütün kaynaklarda en tehlikeli hata türü olarak bahsedilir. Küçük miktarda oluşum gösteren hatalardır. Ölçüleri bazen artı(+) bazense eksi(-) yönde etkiler. Bu hatalar genellikle insan becerisinin sınırlarıyla alakalıdır veya aletin tam yapılamayan ayarlarından kaynaklanır. Bu hataların, diğer iki yöntemde kullanılan yöntemleri kullanarak düzeltilmesinin imkânı yoktur fakat bu hataların belli sınırlar içinde tutulması mümkündür. Hatanın dağıtılması suretiyle aşılabilir.

Sonuç olarak,

1. Bir ölçü ile bir bilinmeyenin gerçek değerine ulaşmak mümkün değildir.
2. Yapılan her ölçüm içinde hata barındırır.
3. Mevcut hatalardan belli bir bölümü önlememektedir.
4. Bir ölçümle gerçek değer değil, birçok ölçümle kesin değer belirlenebilir.

Çıkarımları yapılabilir.

Ölçme ve Kaos

Yapılan ölçümler bir sistem gibi düşünülürse bu sisteme etki eden birçok hata türü vardır. Ölçmede her zaman aranılan ölçüt doğruya en yakın olan sonuçları bulmaktır. Zaten bu durum Kaos’un kendisini bilfiil açıklamaktadır çünkü bunun adı belirsizliktir ancak bu durumda “hiçbir ölçüm işe yaramaz, doğru değil” gibi çıkarımlar yapılması da anlamsız olacaktır. Önemli olan şey ölçmede hata sınırına bağlı kalınıp kalınmadığı ve bu ölçümün yapılma sebebidir. Eğer topçu birliklerinin kullanımına sunulacak bir harita yapılması maksadıyla ölçüm yapılıyorsa, yapılacak santimetre, desimetre düzeyinde hataların çok bir etkisi olmayacaktır çünkü top mermisi 2 metrelik bir hataya göre atılsa bile tesir alanından kaynaklı olarak, istenilen bölgeyi de etkisi altına almış olacaktır. Fakat ölçüm tektonik hareketler için yapılıyorsa yapılan ölçüm o kadar hassas olmalıdır ki santimetre değil milimetre hatta milimetre altı seviyede doğruluk bile önem arz etmektedir. Çünkü tektonik hareketlerin tespitinde yapılan ölçümler fay hareketlerinde, yer kabuğunun hareketlerinde elde edilen verilerse deprem tahmininde aşırı derecede işe yaramaktadır ve hareketler çok küçük boyutta meydana gelmektedir. Ufak hatalar bile ölçmeyi çok yanlış sonuçlara götürebilmektedir. Bu durumu kelebek etkisiyle ilişkilendirmeden geçmek yanlış olur. Ölçümde yapılacak çok küçük bir yanlış, deprem tahmininin belki çok daha ileri tarihlerde tahmin edilmesine, bu da önlem alınmamasına ve bir sürü can ve mal kaybına sebebiyet verebilecektir. Kelebeğin çırptığı kanat kadar küçük bir yanlış, fırtınaların meydana getirdiği hasar kadar kayba sebebiyet veren büyük bir depremle, büyük zararlara neden olacaktır. Ölçümlerde hata kaynaklarından bahsedilmişti. Çelik şerit metreyle ölçüm yaparken ortamdan kaynaklanan faktörler ele alınacak olunursa sıcaklık, basınç, çelik şerit metrenin yapıldığı materyal, vs. birçok bağımsız değişken vardır ve yapılan ölçümler de bu değişkenlere bağımlı olan değişkendir. Kaos teorisine göre sistemde ne kadar çok değişken varsa o sistemin çözümü bir o kadar da imkânsızdır. Kaos teorisi eğer ölçmeyle ilişkilendirilecek olunursa çevresel faktörler sistemi etkileyen değişkenler gibi düşünülebilecektir ve ölçümlerin tam manasıyla doğru (hatasız) çıkması imkânsız olacaktır(sistemin çözümü imkânsız). Doğru yani tam manasıyla, ölçümde her seferinde aynı değer çıkması için gereken şartlar bilindiği kadarıyla hava basıncının hep aynı olması, sıcaklığın hiç değişmemesi veya ölçüm yapılan aletin sıcaklık gibi çevresel faktörlerden hiç etkilenmemesiyle mümkün olabilir. Ölçüm yapan personele de başarmasının imkânsız olduğu, yetenekleriyle alakalı birçok görev düşmektedir. Bu imkânsızlıklar çerçevesinde ölçmenin hatasız olamayacağı Kaos Teorisi’yle açıklanmıştır.

Sonuç

Kaos Teorisi birçok bilim dalını etkilemiştir. Başta fizik kimya gibi sayısal bilimler olmak üzere sosyal bilimlere bile sıçrayan geniş yelpazeli bir kuramın ölçme bilgisi ve metroloji üzerine etkisinin olmayacağını veya ilişkilendirilemeyeceğini düşünmek çok büyük bir yanlış olacaktır. Kaos Teorisi bu konuda bazı dersler çıkarılması için yardımcı olabilir. Ölçmede kesin ve net sonucun bulunamayacağını, hatasız ölçümün olmadığı belirtilmiştir. Yani ölçümde doğru olan değeri bulmak için vakit kaybetmenin anlamsız olduğunu, sadece daha hassas sonuçlar bulunması gerektiğini ders almak gerekmektedir. Kaos Teorisi’ne göre “sistemin çözümü imkânsızdır.” yargısı aynen ölçme adına da içinde çok değişken bulunduğundan geçerlidir. Aynı zamanda yapılan hataların tekrar edilmesi fraktalın adımını artıran iterasyonlara benzetilebilir ve bu fraktalı dallandırır. Ölçümün doğruya daha yakın yapılabilmesi için “hata fraktalının” iterasyonunun durdurulması ve dallanmanın engellenmesi gerekir. Hassasiyet gerektiren ölçümlerde çok küçük detaylara bile dikkat edilmelidir yoksa bu durum çok büyük felaketlerin ortaya çıkmasına, ölçümün çok farklı yerlere sapmasına sebep olabilecektir. Kelebek etkisi konusu hassasiyet isteyen ölçümlerde çok önemlidir. Sonuç olarak Kaos, insanlık ve ölçümleri var olduğu sürece insanlıkla beraber varlığını sürdürecek ve birden fazla değişkenin olduğu bütün sistemleri içine alıp etkileyecektir. Bu durum da Kaos’u daha “kaotik” hale getirecektir.

Kaynakça

1. KARAÇAY, T. (2004). Determinizm ve Kaos. Mantık, Matematik ve Felsefe 2’nci Ulusal Sempozyumu (s. 6). Ankara: Başkent Üniversitesi.
2. RUELLE, D. (1998). Rastlantı ve Kaos. (s. 60-61). Ankara: TÜBİTAK Popüler Bilim Kitapları.
3. KARAÇAY, T. (2004). Determinizm ve Kaos. Mantık, Matematik ve Felsefe 2’nci Ulusal Sempozyumu (s. 6). Ankara: Başkent Üniversitesi.
4. ERTÜRK, A. (2012). Kaos Kuramı: Yönetim ve Eğitimdeki Yansımaları. Kastamonu Eğitim Dergisi, 849-868.
5. ÇOBANOĞLU, F. (2008). Değişim mantığını anlamak: Akış ve dönüşüm olarak örgüt. Pamukkale Üniversitesi Eğitim Dergisi, 23.
6. GLEICK, J. (2000). Kaos: Yeni Bir Bilim Teorisi (F. Üçcan, Çev., s. 25). içinde İstanbul: Tübitak Popüler Bilim Kitapları.
7. METRE’NİN GEÇMİŞİNDE BİR KÜÇÜK GEZİNTİ. (2016, Mart 9). Metroloji Okulu: metrolojiokulu.com/metroloji.htm adresinden alındı.
8. METRE’NİN GEÇMİŞİNDE BİR KÜÇÜK GEZİNTİ. (2016, Mart 9). Metroloji Okulu: metrolojiokulu.com/metroloji.htm adresinden alındı.
9. METRE’NİN GEÇMİŞİNDE BİR KÜÇÜK GEZİNTİ. (2016, Mart 9). Metroloji Okulu: metrolojiokulu.com/metroloji.htm adresinden alındı.