Liseyi okuyupta Logaritma hesabına yabancı olan pek nadirdir. Özellikleri, işlemleri ve bazı ispatları hem zevkli bir o kadar da düşündürücü… Logaritmanın kurucusu John Napier 1550 yılında İskoçya’da doğdu. Ailesi varlıklı ve saygındı. Belki de matematik ile uğraşması bu yüzdendi. Eskiden elit bir uğraştı. Din ile çok yakından ilgilenmiş daha çocuk yaşlarda İskoçya’da gittiği kolejde birçok din kitabını okumuştur. İlk yayınlanan eseri de bu bağlam doğrultusunda bir din kitabı olmuştur. 13 yaşında girdiği kolejde okuduktan sonra Andrew Üniversitesine girdi. Fakat girdiği bölüm matematik üzerine değil, din felsefesi üzerineydi. Napier, matematiği hayatı boyunca amatör bir şekilde oluşmuştur. Zaten matematiği hep bir macera olarak tanımlamış ve bulduğu tüm matematiksel icatların ya da keşiflerin (Matematik Felsefesindeki büyük bir sorun Matematiğin keşif mi icat mı olduğu sorusudur.) bir merak sonucu ortaya çıktığını söylemiştir. (AMS – Reference)
John Napier Avrupa’da eğitim için bir çok yere gittiği söylenmektedir. 22 yaşında Avrupa’dan İskoçya’ya döndüğünde hemen evlendi. Evlendiği kadın İskoç Matematikçi James Sterling’in kızı Elizabeth Stirling olmuştur. Fakat bu evlilik eşinin vefatı nedeniyle fazla uzun sürmemiştir. 2 çocuğu ilk evliliğinden, 10 tane de ikinci evliliğinden çocuğu olmuştur.
Babasının soylu olması ve “Baron” dediğimiz elit bir kesimi temsil ettiği için politika ile de yakından ilgilenmiştir. Fakat herşey üzerinde çalıştığı sayı sistemlerinde bir fikir patlaması sonucu değişti.
1 – 2 – 3 – 4 – 5 – 6
10 – 100 – 1000 – 10000 – 100000
şeklinde bir dizgi onu logaritma denilen bir matematiksel ifadenin çıkmasına zorladı. Birinci dizi aritmetik dizi biçimde iken ikinci dizi geometri bir diziydi. Bunun üzerine John Napier bu bulduğunu iki üniversiteye gönderdi fakat red cevabı aldı. Ama bu işin peşini hiç bırakacak bir insan da değildi. Yukarıdaki sistemi biraz daha geliştirdi ve “Logaritma cetvelini” hazırladı. Bu detaylı cetveli ve bazı açıklamaları ifade eden çalışmasını bir kez daha gönderdi. İşte şimdi başarmıştı. Çalışmayı kontrol eden matematikçilerin çok hoşuna gitmiş, ilk göndermesinin başarısız sayılmasının nedeninin ise “Anlaşılamamış” olmasından kaynaklandığını belirtmişlerdir.
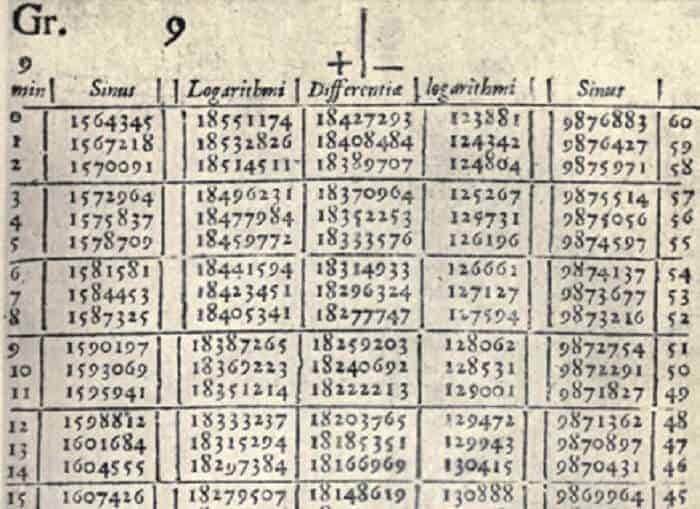İlerleyen yıllarda “Logaritma Cetveli” çok büyük ve çok küçük sayıları kullanan bilim insanlarının geçim kaynağı haline gelecekti. Kopernik (Copernius) gibi bir astronom, Logaritmik cetvelin olmaması halinde büyük bir çalışmasının olamayacağını ifade etmiştir. İlerleyen yıllarda oluşan depremler ile ilgili de logaritma baz alınarak hesaplama olanağı oluşacaktır.
Bir logaritma taban ve kökten oluşur. Bir örnek verirsek 1000 sayısı 3 tane 10 sayısının çarpıdır. 10 tabanında 1000 sayısı ise 3 eşit olacaktır. Yani üstel fonksiyonun tersi biçiminde algılanabilir ki yanlış da sayılmaz. Daha detaya girmemize gerek yok… Matematiksel olarak ise;
biçiminde ifade edilir ve buradaki
eşitliği söz konusu olacaktır. Dolayısıyla;
olacaktır ve
eşitliğinden c=3 çıkacaktır. (Pek ilginç değil sanki)
Ayrıca John Napier evde (ev dediğimiz bir kaledir. Zengin olduklarından dolayı kendilerinin kalesi vardır. Kimseye kısmet olmaz.) kimseye göstermediği, tahtların üzerine bir takım çarpma bölme gibi basit işlemleri gösteren ifadeler yapıyordu. Bunlar ölümünden sonra bulunmuş ve kendisinin ismine atfedilip “Napier Kemikleri – Napier Bones” ismiyle yerini almıştır. Belki üst düzey matematikçiler için pek bir araştırma konusu açacağını tam bilmesek de matematiği yeni öğrenen çocuklar için güzel bir matematiksel nesnedir.
Napier Kemiklerinde 10’a kadar sayılar yazar. Aslında bakarsanız bir abaküsten farkı yoktur. Fakat genel anlamda tüm işlemleri yapabilirsiniz. Abaküs, bir tahta ve bir çerçeveden oluşur. Tahtanın sol kenarı 1’den 9’a kadar sayıları içeren 9 kareye bölünmüştür. Napier’in ahşap çubukları (kemikleri) üzerinde 9 kare vardır. En üstteki kare hariç diğer kareler köşegenleri çizilerek ikiye ayrılmıştır. En üstteki karede tek rakam vardır. Diğer karelerde en üstteki rakamın 2, 3, 4, 5, 6, 7, 8 ve 9 katı yer alır. Bu nedenle bu karelerde iki rakam bulunur. Bu kareler, köşegenleri yardımıyla ikiye ayrıldığından bu iki rakam, biri köşegenin üstünde diğeri altında olacak şekilde yazılır. Ve bu set, 0 ve 9 arasındaki sayıları içerdiğinden 10 çubuktan oluşur. (Napier’in Kemikleri’nin güncel versiyonunda tüm kareler ikiye ayrılmıştır. Tek basamaklı sayılar başlarına 0 eklenerek karelere yazılır.)
Napier ise bu matematiksel buluşların ardından 1617 yılında yine İskoçya’da ölmüştür. Ölüm nedeni ise “Gut” hastalığı denilen ve halk arasında “Kral hastalığı ya da Zengin hastalığı” şeklinde bilinen hastalıktan kaynaklanmıştır. Aileye yakışan bir ölüm…