İmpuls ve Momentum Nedir

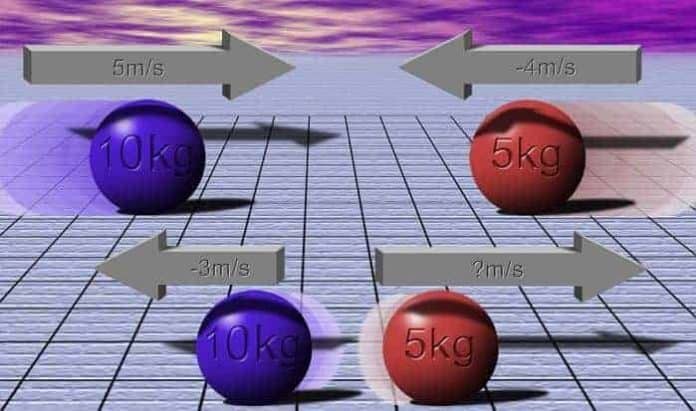
Merhaba arkadaşlar bu yazımızda sizlere impuls ve momentum kavramlarını anlatacağım, bunun yanısıra impuls ve momentum teoremi olarak bilinen bu ifadenin newtonun ikinci yasası ile bağını örneklerle açıklayacağım. Üzerine kuvvet uygulanan bir parçacığın momentumunun değiştiğini gördük. Bunu bilmek, pek çok problemin çözümünü kolaylaştırır. Bir parçacık üzerine zamanla değişen bir F kuvveti uygulanırsa bu önemli kavramı daha iyi anlayabiliriz. Newton’un ikinci yasasına göre F = dp/dt veya

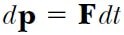
olur. Kuvvet belli bir zaman aralığında uygulanmış ise, momentum değişimini bulmak için bu ifadelerin integralini alırız. Parçacığın momentumu t_i anındaki p_i değerinden t_f anında p_f değerine değişirse, 1 Eşitliğin integrali aşağıdaki şekli alır:

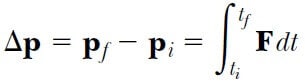
İntegrali hesaplamak için kuvvetin zamanla nasıl değiştiğini bilmemiz gerekir. Bu eşitliğin sağ tarafındaki niceliğe, Δt= t_f – t_i zaman aralığında parçacığa et­kiyen F kuvvetinin impulsu denir. İmpuls, aşağıdaki şekilde tanımlanan bir vektördür:

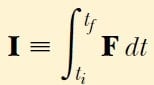
Bir parçacık üzerine etkiyen F kuvvetinin impulsu, bu kuvvetin sebep olduğu parçacığın momentumundaki değişime eşittir.

İmpuls ve Momentum Teoremi

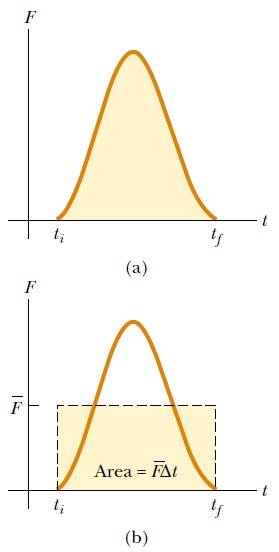
İmpuls ve momentum teoremi olarak bilinen bu ifade, Newton’un ikinci yasası­na eşdeğerdir. Bu tanıma göre, Şekil 1a’da belirtildiği gibi impulsun, kuvvet- zaman eğrisi altındaki alana eşit büyüklükte bir vektörel nicelik olduğunu gö­rürüz. Bu şekilde gösterildiği gibi, kuvvetin zamanla değiştiği ve Δt= t_f – t_i zaman aralığında sıfır olmadığı varsayılıyor, impuls vektörünün yönü momen­tum değişiminin yönü ile aynıdır. Boyutu da ML/T şeklinde momentum boyutundadır. İmpuls, parçacığın kendi başına bir özelliği olmayıp, uygulanan dış kuvvetin, parçacığın momentumunu değiştirmesiyle ilgili bir niceliktir. O halde, parçacığa bir impuls verilmesi, kuvvet uygulayan kaynaktan parçacığa mo­mentum aktarılması demektir.

Genel olarak kuvvet zamanla değişebildiğinden, aşağıdaki şekilde ortala­ma bir F kuvveti tanımlamak uygun düşer:

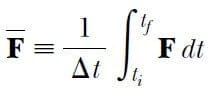
burada, Δt= t_f – t_i dir. (Bu, yüksek matematikteki ortalama değer teoreminin bir uygulamasıdır). 3. Eşitlik şu şekilde yazılabilir:

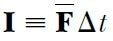
Şekil 1b’de tanımlanan bu ortalama kuvvet, parçacığa Δt zaman aralığında değişen gerçek kuvvetin impulsuna eşit impuls veren sabit bir kuvvet olarak düşünülebilir.

İlke olarak, F zamanın fonksiyonu olarak bilinirse; impuls, 3.Eşitlikten hesaplanabilir. Parçacığa etkiyen kuvvetin sabit olması halinde hesaplama ol­dukça basit olur. Bu durumda F = F dir ve 5. Eşitlik şu hale gelir:

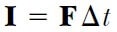
Pek çok fiziksel durumda, impuls yaklaşımı ifadesini kullanacağız. Bu yaklaşımda, bir parçacık üzerine uygulanan kuvvetlerin birinin kısa bir süre etki ettiği, fakat mevcut diğer kuvvetlerden daha büyük olduğunu varsayarız. Bu yaklaşım, özellikle çarpışma süresi çok kısa olan çarpışma olaylarında kullanışlıdır. Bu yaklaşımda kuvvete, impulsif kuvvet deriz. Örnek olarak, bir beysbol topunun beysbol sopasına çarpma süresi 0,01 s civarındadır ve bu zaman aralığında, sopanın topa uyguladığı ortalama kuvvet birkaç bin newton kadardır. Bu da kütle çekim kuvvetinden daha büyüktür ve böylece impuls yaklaşımı da doğrulanır. Bu yaklaşım kullanılırken p_i ve p_f’nin çarpışmadan hemen önce ve sonraki momentumlar olduğuna özellikle dikkat etmek gerekir. Bu nedenle impuls yaklaşımında, çarpışma sürecince parçacığın hareketi çok küçük olur.

Bu yazımızda sizlere impuls ve momentum kavramlarını anlattım. Diğer yazımızda bu konunun devamı olan çarpışmaları anlatacağım. Diğer yazımızda görüşmek üzere.