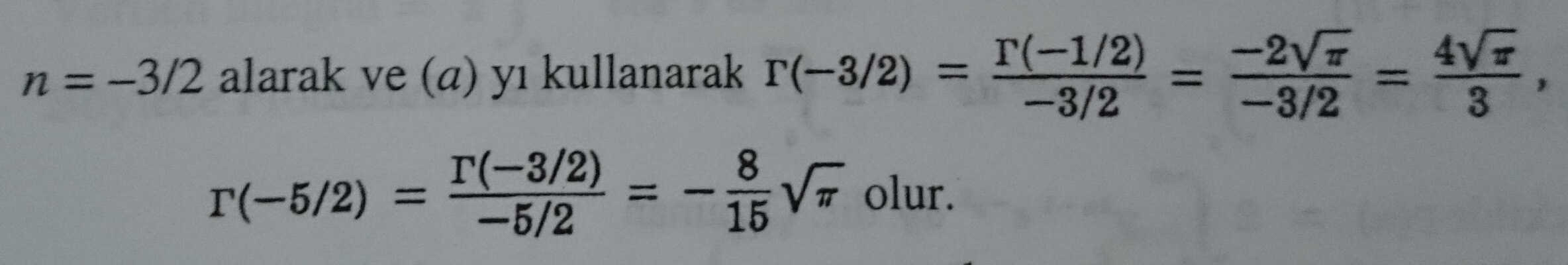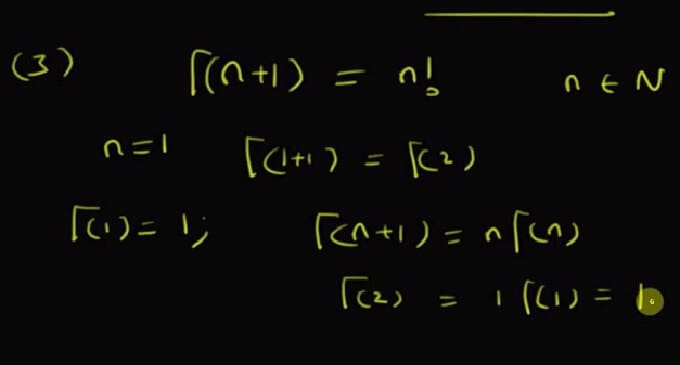Gama Fonksiyonu ve Özellikleri

Bu yazımızda sizlere gama fonksiyonu ve özelliklerini anlatacağız. Bunun yanı sıra konuyu daha iyi kavraya bilmek için gama fonksiyonu ile ilgili çözümlü örnekler çözeceğiz. Γ(n) ile gösterilen Gama fonksiyonu.

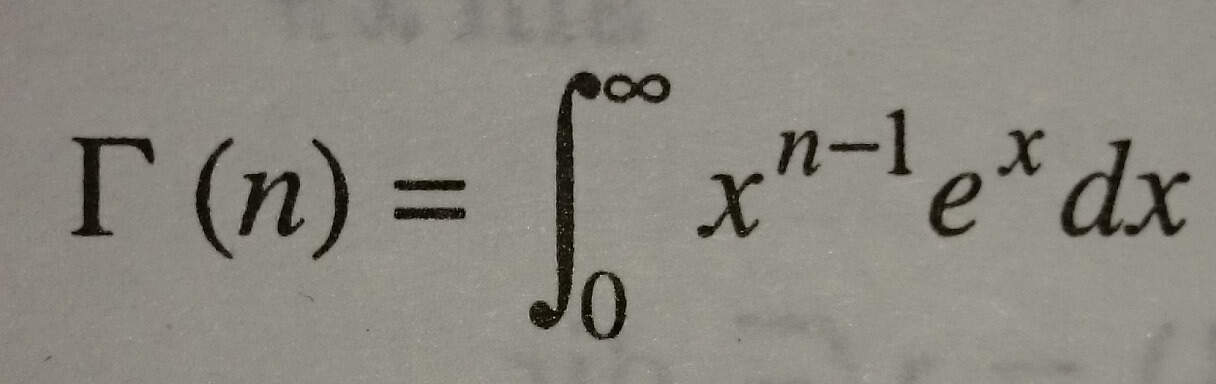
ile tanımlanır ve n>0 için yakınsaktır.

Gama fonksiyonu için yenilenim formülü

Γ(n + 1) = n Γ(n)   (Eşitlik 2)

dir. Burada Γ(1) = 1 dir. 1 ≤ n < 2 için (veya birim uzunluklu herhangi bir aralık) değerleri bilindiği zaman (2) den Γ(n) tüm n>0 için belirlenebilir (aşağıdaki tabloya bakınız). Özel olarak, eğer n bir pozitif tamsayı ise, o zaman

Γ(n+1) = n!  n = 1, 2, 3 … (Eşitlik 3)

olur. Bu nedenle bazen Γ(n) faktöriyel fonksiyonu olarak adlandırılır.

Γ(2) = 1! = 1 , Γ(6) = 5! = 120

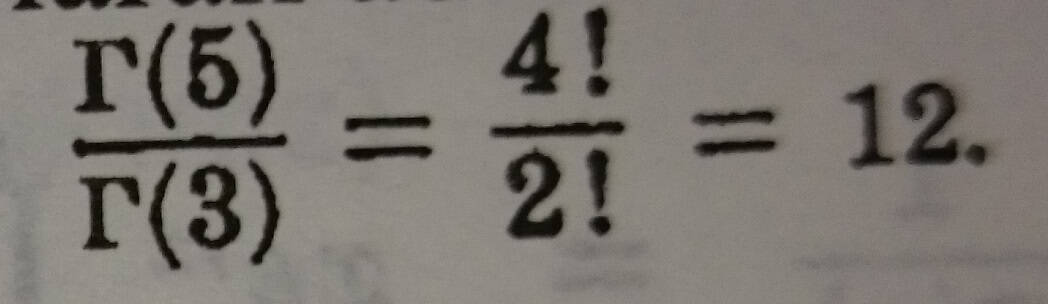
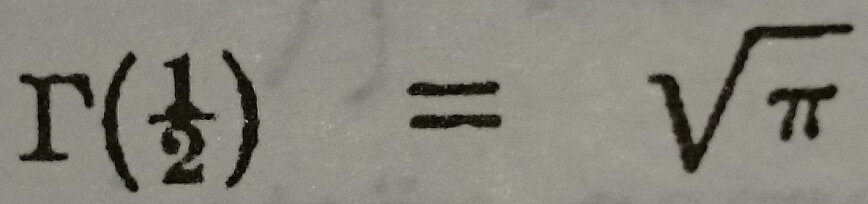
olduğu gösterilebilir.

Eşitlik 2 yenilenim bağıntısı bir fark denklemi olup çözümü Eşitlik (1) dir. n > 0 için Eşitlik (1)’ i Γ(n) nin tanımı alarak ve Eşitlik (2) yi

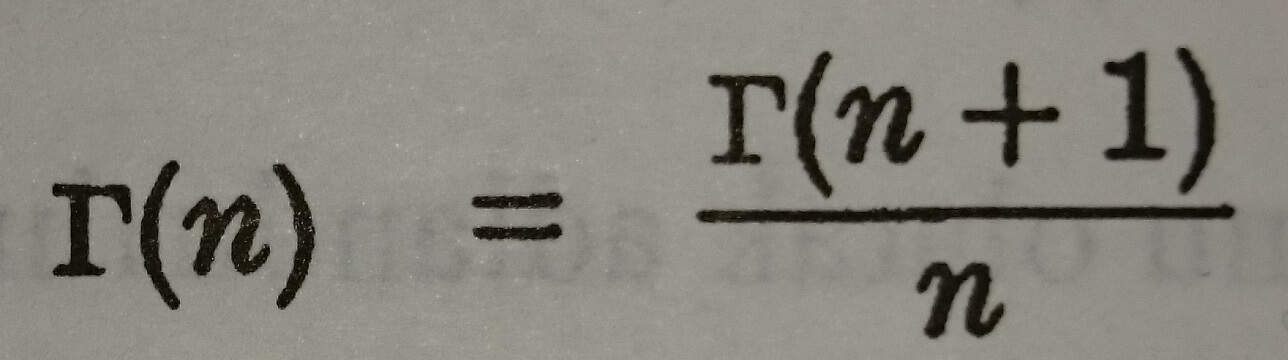
şeklinde kullanılarak gama fonksiyonunu n < 0 a genişletebiliriz.

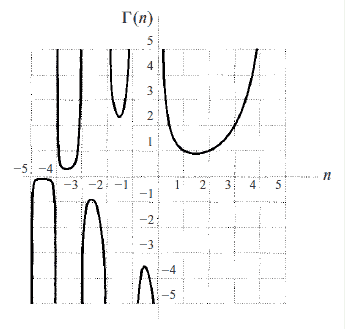
Gama Fonksiyonunun Değerler Tablosu ve Grafiği

Γ(n) İçin Asimtotik Formül

Eğer n büyük ise Γ(n) nin hesaplamasındaki zorluklar belirgin olarak ortaya çıkar. Böyle bir durumda kullanışlı bir sonuç

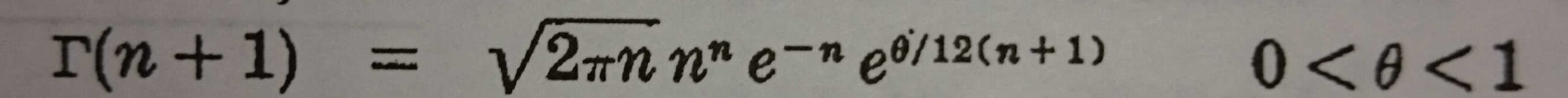
bağıntısıyla sağlanır. Pek çok pratik amaçlar için, n büyüdükçe 1’e yaklaşan son çarpan ihmal edilebilir. Eğer n bir tamsayı ise

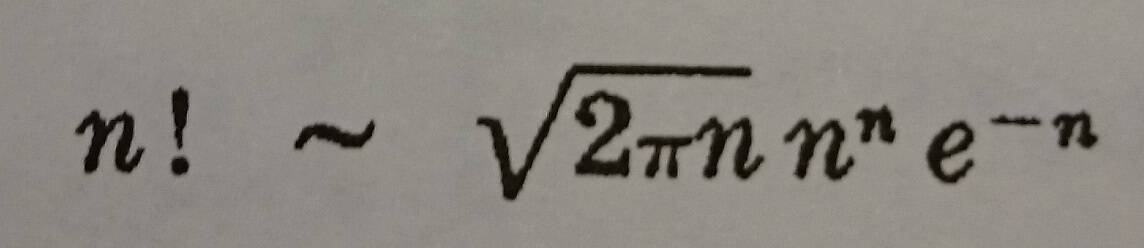
yazabiliriz. Burada ∼ nin anlamı “büyük n için yaklaşık olarak eşit” anlamını taşır. Bu bazen Stirling yaklaşık faktöriyeli veya n! için asimtotik formülü olarak adlandırılır.

Gamma Fonksiyonunu İçeren Çeşitli Sonuçlar

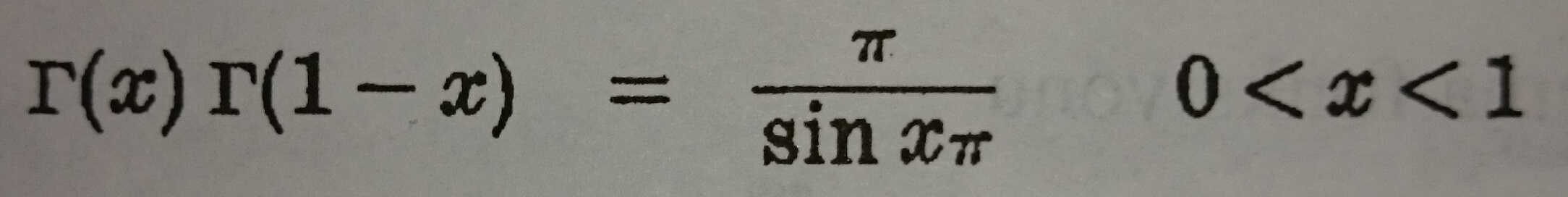
Özet olarak eğer x = 1/2, ise

dir.

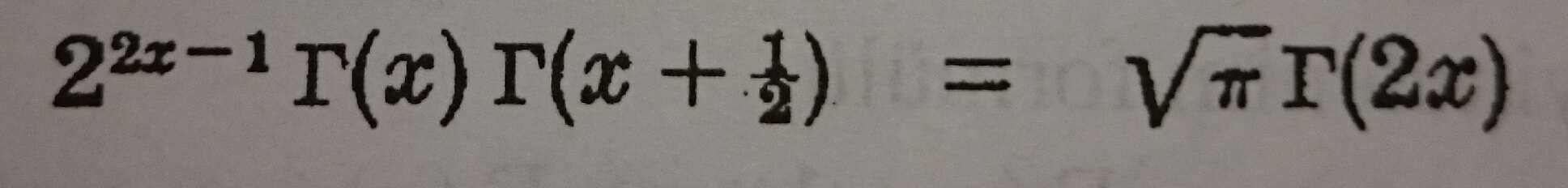
Bu, gama fonksiyonu için çoğaltma formülü olarak adlandırılır.

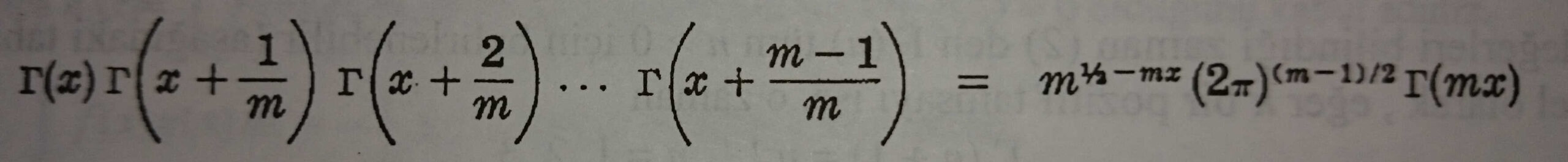
Eşitlik (9) sonucu Eşitlik (10)’ un m = 2 için bir özel durumudur.

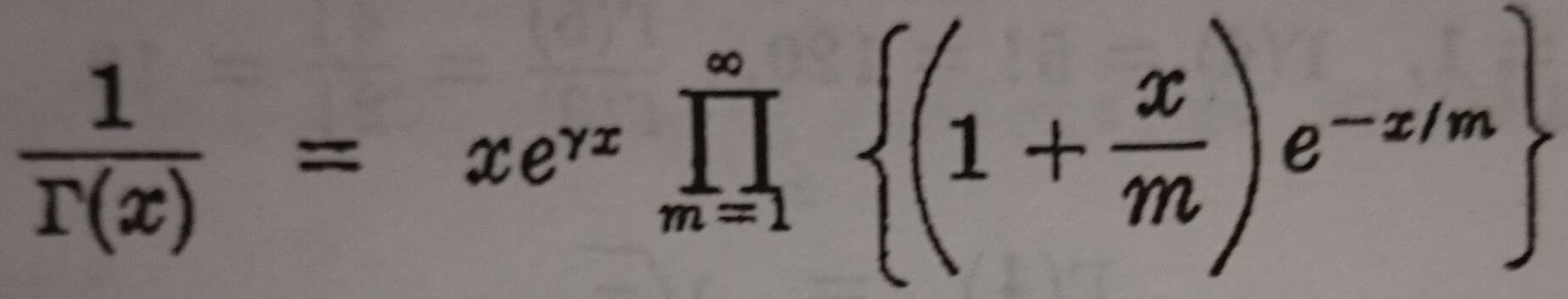
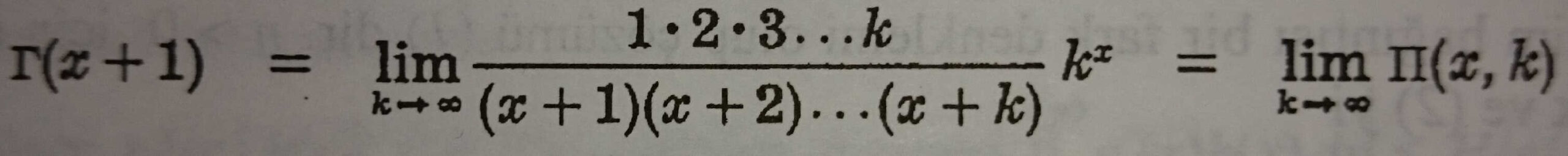
Bu, gama fonksiyonu için bir sonsuz çarpan gösterimidir. γ sabiti Euler sabitidir.Burada ∏ (x, k) bazen Gauss ∏ fonksiyonu olarak adlandırılır.

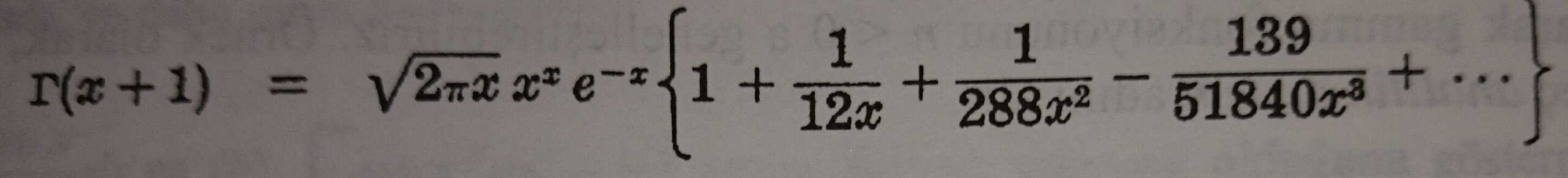
Bu seriye gama fonksiyonu için Stirling asimtotik serisi denir. Parantez içindeki seri bir asimtotik seridir.

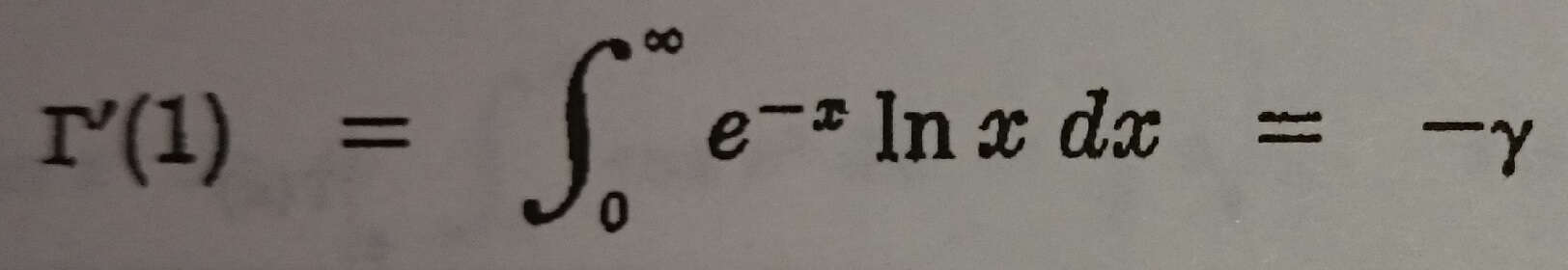
burada γ Euler sabitidir.

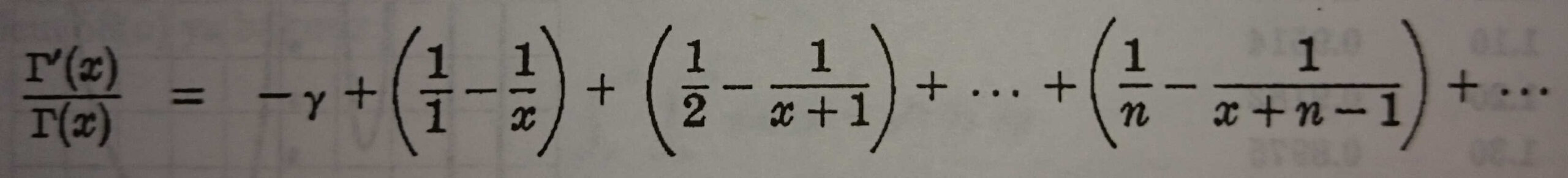
Gama Fonksiyonu İle İlgili Çözümlü Örnekler

1. (a) Γ(n+1) = n Γ(n), n > 0; olduğunu ispatlayınız.

Eğer n>0 ise;

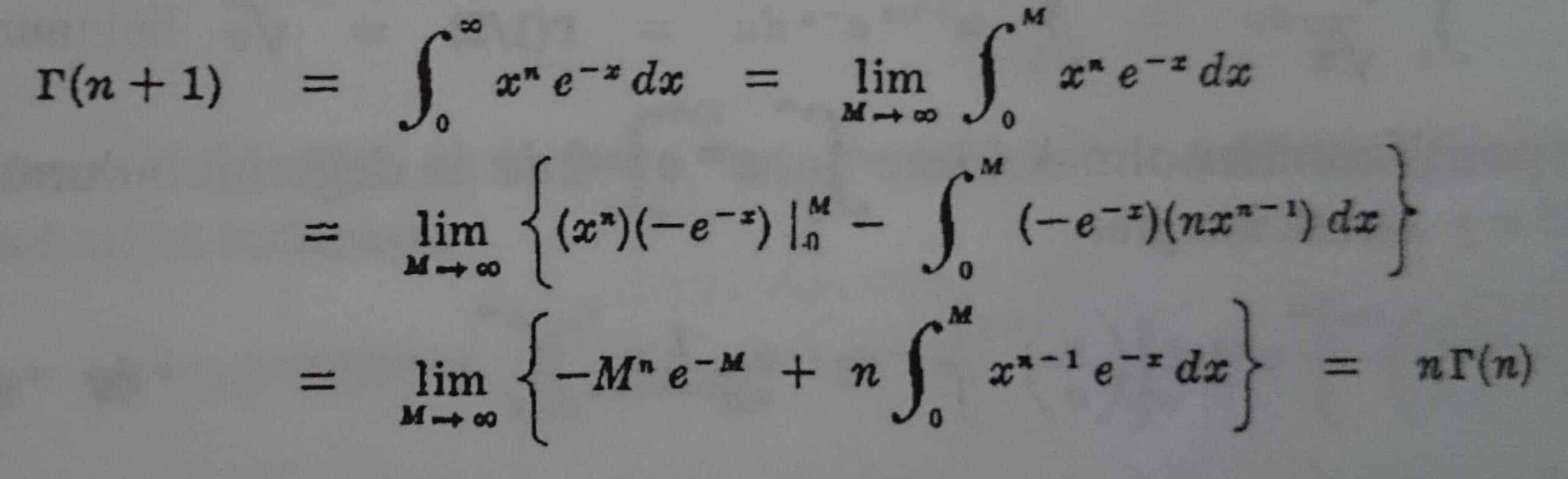
olur.

(b) Γ(n+1) = n!, n = 1, 2, 3 … olduğunu ispatlayınız.

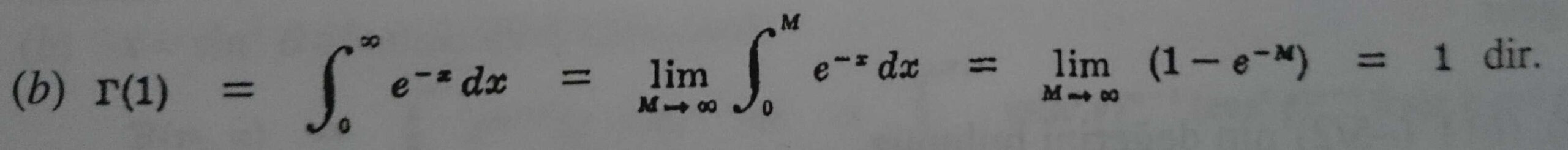
Γ(n+1) = nΓ(n) ‘de, n = 1, 2, 3 …koyunuz. O zaman

Γ(2) = 1Γ(1) = 1, Γ(3) = 2Γ(2) = 2.1 = 2!, Γ(4) = 3Γ(3) = 3.2! = 3!

Genel olarak, eğer n bir pozitif tamsayı ise Γ(n+1) = n! dir.

2.Aşağıdaki herbirinin değerini bulunuz.

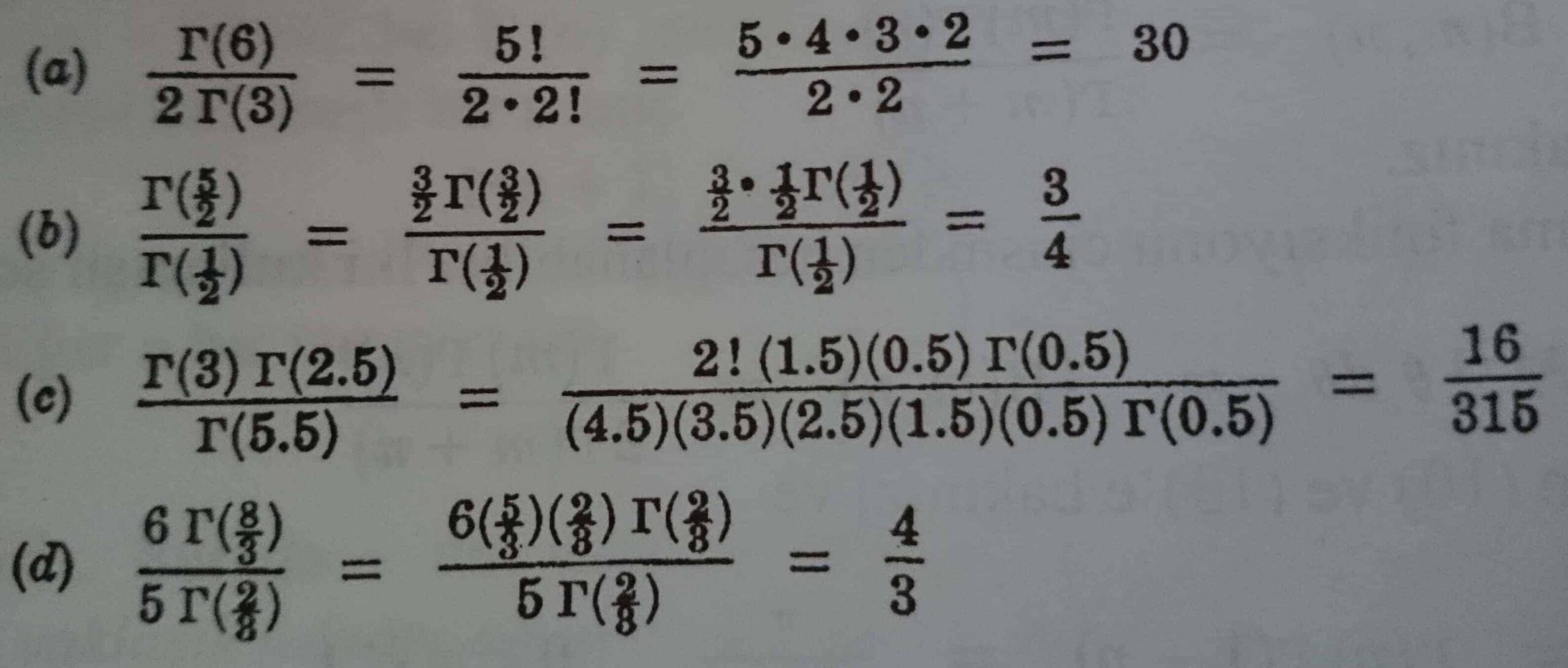
3. Aşağıdaki her bir integralin değerini hesaplayınız.

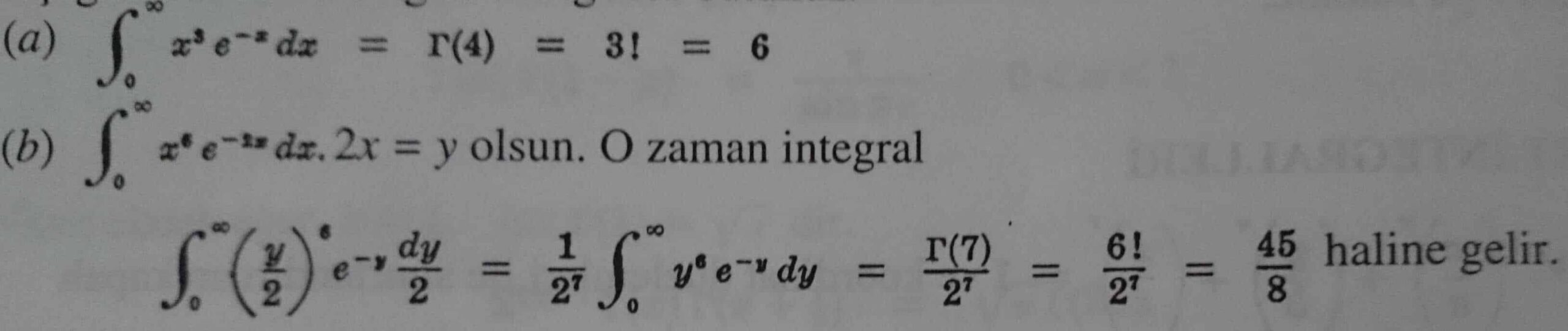
4.  ‘yi ispat ediniz.

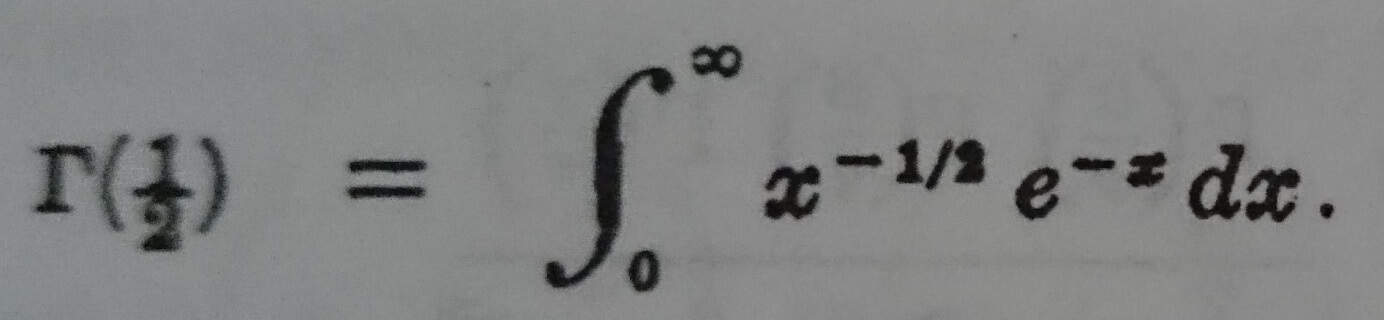
x = u² alınırsa bu integral

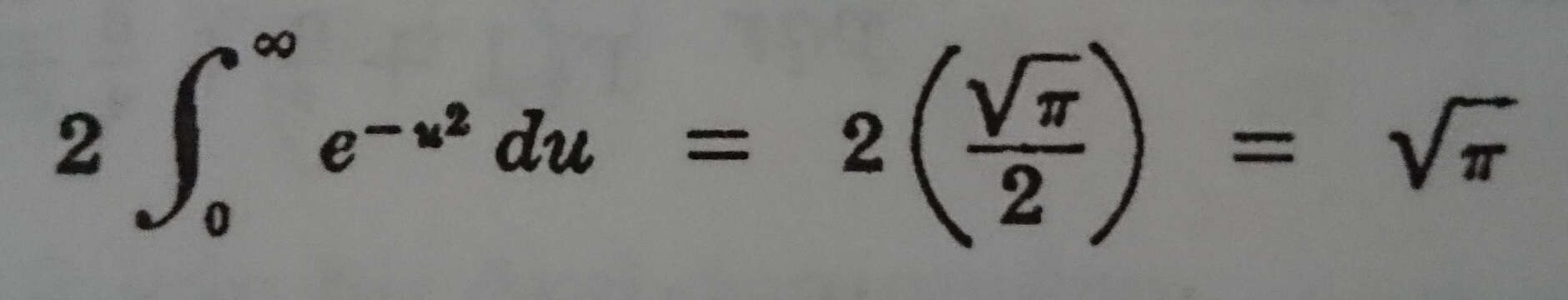
haline gelir.

5. (a) Γ(-1/2) değerini bulunuz.

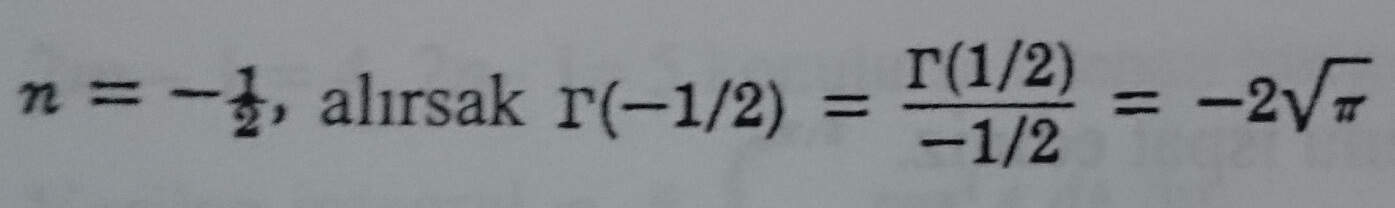
bulunur.

(b) Γ(-5/2) değerini bulunuz.