Fraktal geometri artık matematiğin estetik boyutunu gözler önüne seren sanatsal olduğu kadar matematiksel ifadeleri de içinde barındıran bir matematik dalıdır. Genellikle ilköğretim düzeyindeki öğrencilerin çalışma konusu olsa da aslında bu konu matematikçilerin çok önemli bir çalışma alanıdır. Fraktal, iç içe geçmiş sonsuza uzayan nesneler olarak tanımlanır.
Bu şekiller öklid geometrisi ile açıklanamadığından dolayı, matematikçiler farklı bir modelleme getirerek anlama uğraşına girmişlerdir. Fraktalı sonsuza giden ve kendini yenileyen nesneler olarak bilsek hiçbir sorun oluşturmaz. Fraktallar ile ilgili önemli bir açıklama ise sanatçı Escher’in yaptığı devasa (Büyüklük olarak değil) yapıtlar ile karşımıza çıkmaktadır. Ona göre bir nesnenin fraktal olabilmesi için gerek ve yeter şart nesnenin büyütüldüğünde aslına benzer olmasıdır. Fraktalların başlangıcı Escher ile başladığı varsayılsa da eski yunan matematiğinin, bazı çalışmalarında bu işlerle uğraşıldığı tahmin edilebilmektedir. Asıl mucidini aşağıda açıklayacağız.
Doğadaki Fraktallar
Doğada birçok kez karşımıza çıkan fraktal örneklerin sadece bir tanesi eğrelti otlarıdır. Bir eğrelti otunu alıp mikroskop ile bir parçasına baktığınız zaman, görünen resim bir eğrelti otunun yaprağının aynısıdır. Mikroskopta incelediğiniz o yapının bir parçasını biraz daha büyük bir mercek ile baktığınız da o parçanın da aynı biçimde ilk parçaya benzediği görülmektedir.
Sanki aynı şeyleri söyleyip duruyor gibi görünsekte fraktal geometri belki de yaratıcının doğaya bıraktığı izlerin yansımasıdır. Genellikle sorulan sorulardan bir tanesi olan doğada matematik var mıdır sorusu bu uğraşın yadsınamaz bir parçasıdır. Matematiği matematik yapan da budur işte!
Bilgisayarın gelişmesi ile insanlar bilgisayarlar üzerinden kendi fraktallarını yapmaya başladılar. Bunu yapması zor mudur kolay mıdır en ufak bir fikrim yok fakat bu yapılan fraktalları matematiksel sonsuz seriler ile harmanlayıp matematiğin analiz kısmına göndermişlerdir. Iraksak dizi hesaplayan birçok kişi bu serilerin ne anlam ifade ettiğini hemen anlayabilir.
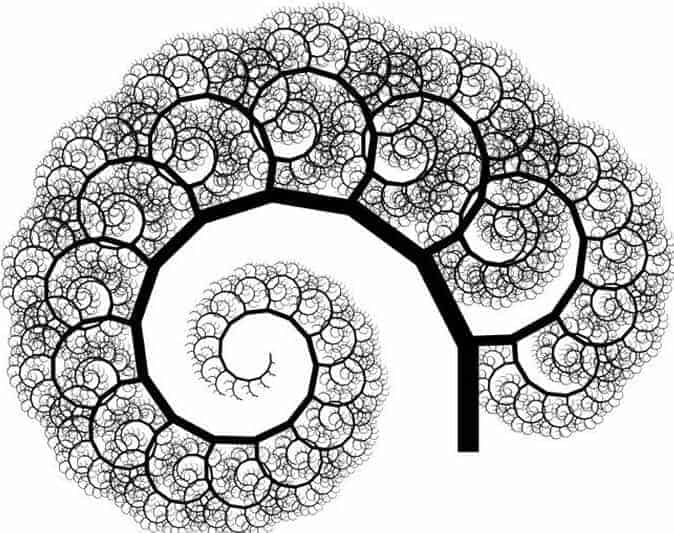Dikkat edilmesi gereken diğer husus ise “sonsuz sarmal” olarak belirtilen şekillerin bir fraktal belirtmediğidir. Bu nesneler iç içe geçmiş çember formatının sonsuza gitmesi ile açıklanır fakat bir fraktal belirtmez evet bir sonsuzluk söz konusu fakat içteki nesne asıl nesneye benzememektedir.
Fraktal ne zaman ortaya çıktı? İlk kim uğraştı? Nasıl bir şekilde ortaya çıktı? gibi soruları yanıtlamaya çalışalım. Aslında fraktalın geçmişi çok da uzun yıllar evveline dayanmaz. 1975 yılında Polonya asıllı matematikçi Benoit Mandelbrot ( asıl mesleği mühendis ) çalıştığı işyerinde bazı veri iletim hatalarını günlük, yarım günlük, saatlik, dakikalık, saniyelik, saliselik zaman kavramlarına böldüğünde sorun çıkaran hataların aynı biçimde tekrar karşısına çıktığını görmüştür. Bu şekilde fraktal tanımı ortaya yapmıştır.
Fraktalların boyutu ile ilgili çok derin konular işlenmekte olup okurla daha ileri seviye fraktal geometrinin matematiksel işlemlerine girmeyi uygun bulmadım. Fakat Kendisinin tam bir kopyasını daha küçük boyutlarda içeren fraktallar için fraktal boyutu ve kendine benzerlik boyutu değerleri aynıdır. Bu bizim için yeterli olacaktır. Fraktal geometrisi artık topoloji bilimi ile de (topolojiyi daha derin işleyeceğiz ) iç içe geçmiş ve bazı önemli kümelerin fraktal boyutları logaritma ile hesaplanmıştır. Örneğin; Cantor Kümesi…