Duyduğunuz sesler – kulaklarınızın algıladığı en minimal ve maksimal sesler de dahil doğada titreşimlerin bir ürünü olarak dalgalanan ses dalgalarının kulaklarımızda bulunan salyangozda aktif hale gelmesi ile sürece girdikten sonra beyne giden sinyallerden sonra da algılama ile bitmektedir. Bu durum aslında birçok kişi için sıradan bir olaydan başka bir şey değil. Dalgalar ve titreşimler üzerine çalışan matematikçiler Fourier dönüşümleri ile çok yakından ilgilenmektedir. Bu konu analiz ve diferansiyel dallarını çalışanların göz bebeği olsa da matematikçi kimliği olan herkesin de ayrıca bildiği bir konudur.
Bu fotoğrafın aslında ne anlatmak istediğini hemen ekranda beliren dalgaların matematiksel olarak okurda ne anlam ifade ettiği ile bağlantılı olacağına eminiz. Lise de öğretilen bir sin(x) fonksiyonun grafiğidir. Elimizde tuttuğumuz demir ve vida biçiminde oval yapı bir ses dalgası üretmeye yarayan yapıdır. Cihaz ise bu oluşan ses dalgalarını ekrana ileterek frekans ayarını ya da şiddetini anlamımıza yarayan iletkendir. Bu yaptığımız aslında en basit ve düzgün Fourier oluşumudur. Fakat bu böyle her zaman kolay olmamaktadır. Daha karışık dalgalar ve titreşimler için matematikçiler nasıl bir yol izliyor?
18. yy‘da Fransa devrim yapan matematikçilerden bir tanesi de hepinizin yakından tanıyacağı – en azından üniversite okurken etrafta bir yerde dedikodusunun geçtiği kişi – Joseph Fourier dalgalar kuramı ile yakından ilgilenmiş basit dalga modellerini trigonometrik fonksiyonların grafiklerine benzetmeye çalışmış, çok daha karmaşık olan diğer titreşimlerin grafiklerini parçalayarak anlamaya çalışmıştır. 100’lerce çalışmanın ardında karmaşık dalgaların modellemesinin parçalayarak daha rahat anlaşılacağını görmüştür ve ölümüne yakın zamanlarda kendi adıyla anılan “Fourier Dönüşümü” adlı makalesini yayınlamış ve resmen matematik dünyasına roket gibi girmiştir. ( Tabir de hiçbir abartı yok). Makaleyi ise önemli kılan şu açıklamadır. “Bir ses dalgasının ifadesi veya zamana bağlı olarak değişen herhangi bir sinyalin, oluşturan sinüs dalgalarının toplamı, o sinyalin Fourier dönüşümü olarak nitelendirilecektir.” Bu çok kesin bir bilgiydi ve zamanla da doğruluğu kabul edilir.
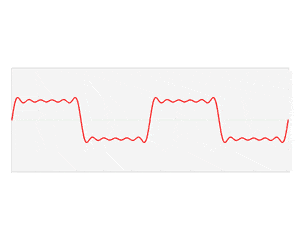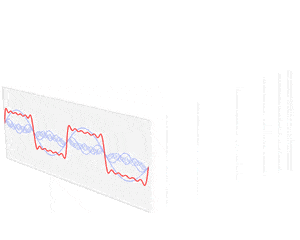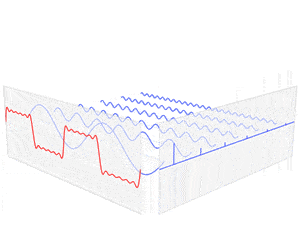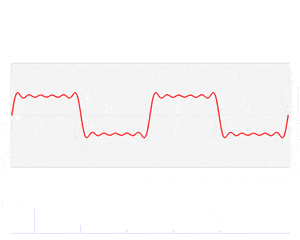
Yukarıda bir dönüşüm görüyorsunuz. F fonksiyonu zaman içinde değişir – bir ses dalgasını temsil eder. Fourier dönüşümü işlemi f’yi alır ve belirli frekanslar ve amplitüdler ile onu oluşturan sinüs dalgalarına dönüştürür. Fourier dönüşümü, frekans alanındaki sivri uçlar olarak temsil edilir; sivri uç yüksekliği, frekans dalgasının genliğini gösterir.
Bununla birlikte, bir görüntüyü değişen bir işlev olarak düşünebilirsiniz; Değişim ise zamana bağlı olarak görüntünün iki boyutlu aralığında değişir. Gri skala sayısal görüntüde, piksellerin her biri 0 ile 254 arasında bir değere sahiptir ve bu pikselin koyuluk derecesini temsil eder. O pikselin karanlığı veya yoğunluğu, o pikselin konumunu veren yatay ve dikey koordinatların bir fonksiyonudur. Görüntüyü piksel değeri ile verilen manzara yüksekliği ile dalgalı bir manzara olarak düşünebilirsiniz.
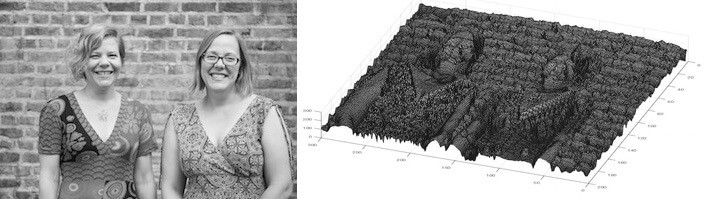Mesela iki araştırmacı olan matematikçilerin sağda dönüşümünü yaptım. Koyu olan yerleri siz yorumlayabilirsiniz.
Görüntüler aynı zamanda sinüs dalgaları toplamı olarak da ifade edilebilir, ancak bu kez tek boyutlu dalgalar yerine iki boyutta dalgalanan dalgalar, örneğin bir sayfadaki dalgalar gibi.
İki boyutlu sinüs dalgaları şu şekilde yazılır:
Z = a sin (hx + ky)
Burada x ve y, “tabaka” üzerindeki noktalara ait koordinatları verir; z, o noktadaki dalganın yüksekliğidir veya yoğunluğudur; a dalganın genliğini (maksimum yükseklik) verir ve h ve k, Zaman zaman dalga sırasına göre x ve y yönlerinde tekrarlanır (bunlar x ve y frekanslarıdır).
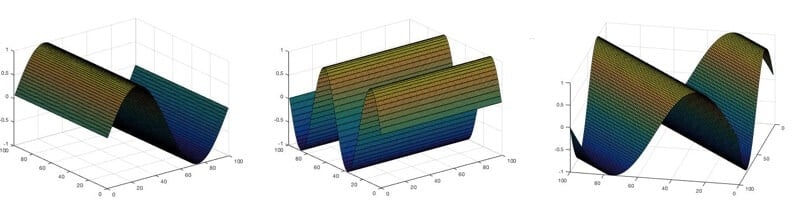Birinci grafik sin(x) grafiği ikinci sin(2x) ve en sağda bulunan son grafik sin(x+y) grafiğidir. Yukarıda bahsettiğimiz değişim meselesini grafikle daha iyi sezebiliriz.
K = 0 olduğunda, sinüs dalgası yalnızca x-ekseni boyunca dalgalanır. H = 0 olduğunda, yalnızca y ekseni boyunca dalgalanır. Ancak hem k hem de h sıfırdan farklıysa, sinüs dalgası sayfanın çapraz olarak hareket eder ve dalgalar eğik h / k ile açılı yönde (dalga ceplerine dik) yönelir.
Bu dalgaları bir araya getirmek sadece her pikseldeki dalgaların ilgili değerlerini veya yüksekliklerini eklemeyi içerir. Dalgalar, o noktada daha yüksek bir değere sahip nihai bir dalga yaratmaya müdahale de edebilir.
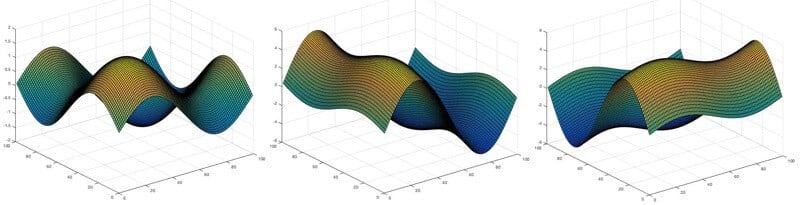Bu grafikler de yukarıda K=0 yada H=0 olayını anlamımıza yardımcı olabilir. Soldaki grafik sin(x+y), ortadaki grafik sin(x)+5sin(y) ve en sağdaki grafik 5sin(x) + sin(y) grafiğidir.
Bir görüntünün Fourier dönüşümü, görüntü fonksiyonunu (dalgalı peyzaj), oluşturan sinüs dalgalarının toplamına bölünür. Bir ses dalgasında olduğu gibi frekansa karşı Fourier dönüşümü çizilir. Fakat bu durumun aksine, frekans alanı, x ve y boyutlarındaki dalgaların h ve k frekansları için iki boyuta sahiptir. Dolayısıyla bir seri sivri uç olarak değil, orijinal görüntü ile (kabaca) piksel cinsinden aynı boyutta bir resim olarak çizilir.
Fourier Dönüşümleri tüm görüntülerin izlerini, tüm ses titreşimlerinin bir matematiksel uyarlamasıdır. Peki nerde kullanılır? Tek bir örnek ise yeter! Böbrek taşlarının kırılması için kullanılan ses titreşimleri Fourier dönüşümü ile hesaplanan ve üretilen bir titreşimdir. Hastanın taş kalınlığı ve tabakasının saptanması ile bu fonksiyonun genlik ve frekans değerleri değiştirilerek yeni bir dalga üretilir. Titreşimler böbrekte bulunan taş için uyarıcı nitelik taşır ve belli bir tedavi sürecinden sonra sağlığına kavuşur. Yaşasın Matematik!