Ford Fulkerson Algoritması Tarihi; Çizge Teoreminin tarihi, 1736 yılında ilk kez Leonhard Euler tarafından çözümlenen, Königsberg’ in 7 köprüsü (graf teorisi nedir) problemi ile başlamaktadır. Birçok problem Euler tarafından bulunan bu teorem üzerinden çözümlenmektedir. Bunlardan birisi de azami akış (max flow) problemidir.
Herhangi bir başlangıç noktasından hedef noktasına olan azami akışı belirlemek için kullanılan Ford Fulkerson Algoritması 1956 yılında L.R Ford ve D.R Fulkerson tarafından bulunmuştur. Günlük hayattaki önemi çok büyük olan bu algoritma kullanıldığı bazı yerler; elektrik devreleri, bilgisayar ağ sistemlerinin optimizasyonu, trafik akışını yönlendirme, elektrik, su ve atık su akışını yönlendirmede kullanılmaktadır.
Algoritmanın sözde kodu (pseudo code):
- İlk artık çizgeyi oluştur (residual graph).
- Residual graph’ ta başlangıç noktasından bitiş noktasına ulaşan yol olduğu sürece
aşağıdaki adımları yap:
a) Başlangıç noktasından bitiş noktasına olan yolu belirle
b) Yol üzerindeki maximum kapasiteyi (δ ) belirle
c) Yol üzerindeki akışı δ değerince arttır
d) Geri dönüş yolundaki akışı δ değerince azalt
Ford Fulkerson Algoritması örnek:
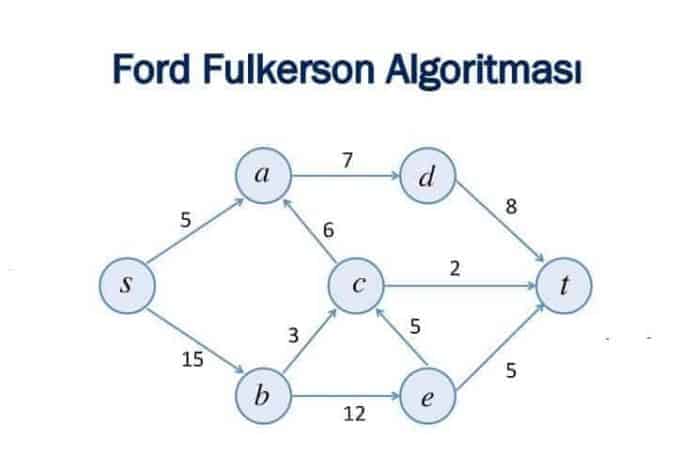
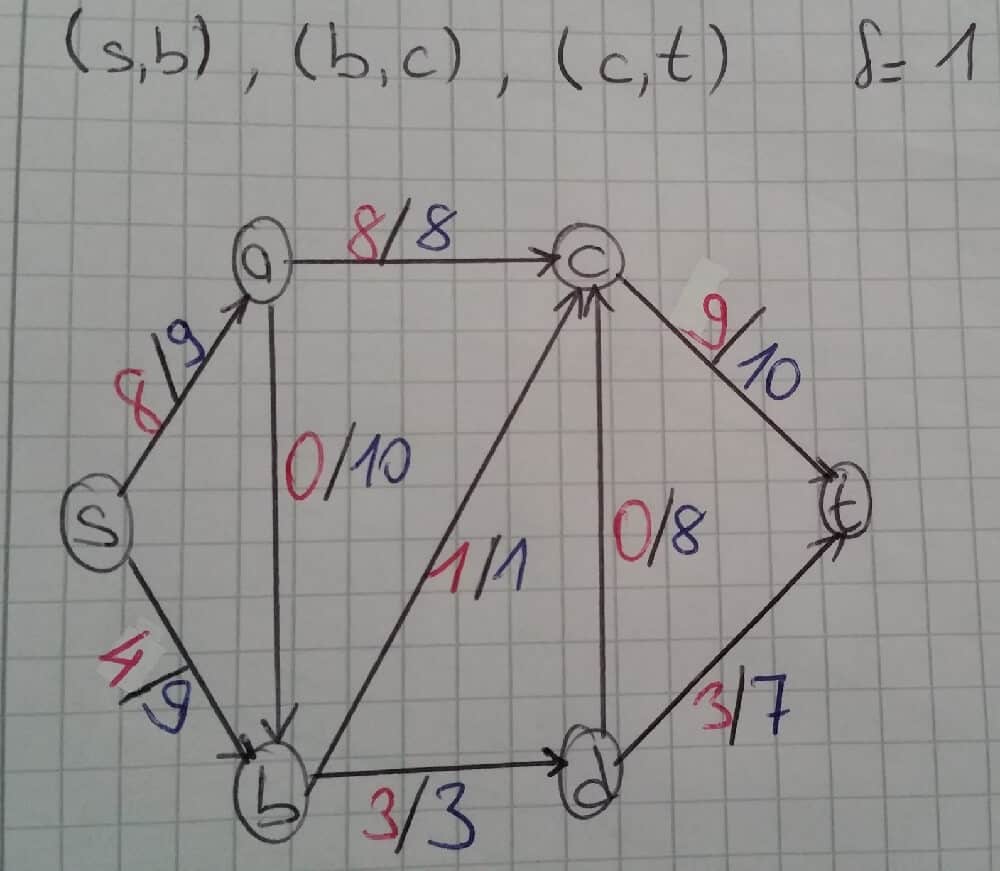
Bir örnek ile algoritmanın çalışmasını inceleyelim. Verilen çizgede s noktasında bulunan arıtma merkezinden t noktasına akan maximum su miktarını bulalım.
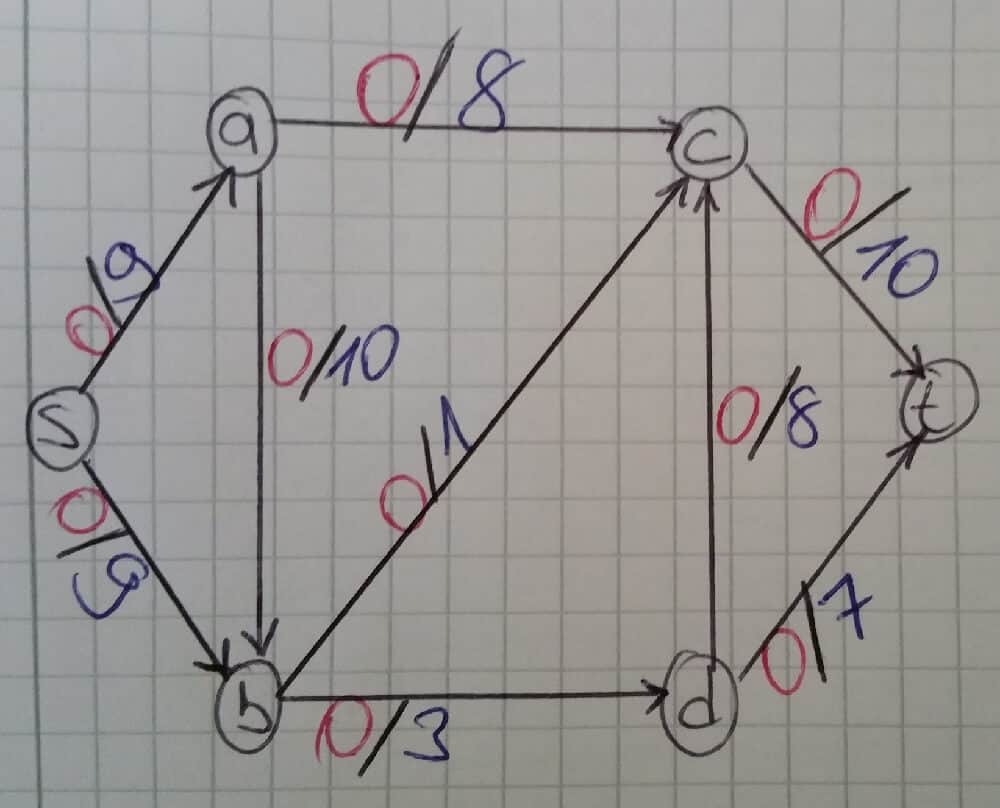
Resimde oklar üzerinde görünen kırmızı değer o anki yol üzerinde bulunan su miktarını, mavi renkli rakamlar ise yolun kapasitesini belirtmektedir. Yani s noktasından a noktasına maximum 9 birim su göderilebilir ancak şuan yol üzerinde bir akış bulunmamaktadır. Aynı şekilde, a-c yolunun kapasitesi 8 birimdir ve bu yol üzerinde de henüz bir akış yoktur. Algoritmanın birinci adımında ilk residual graph belirlenir.
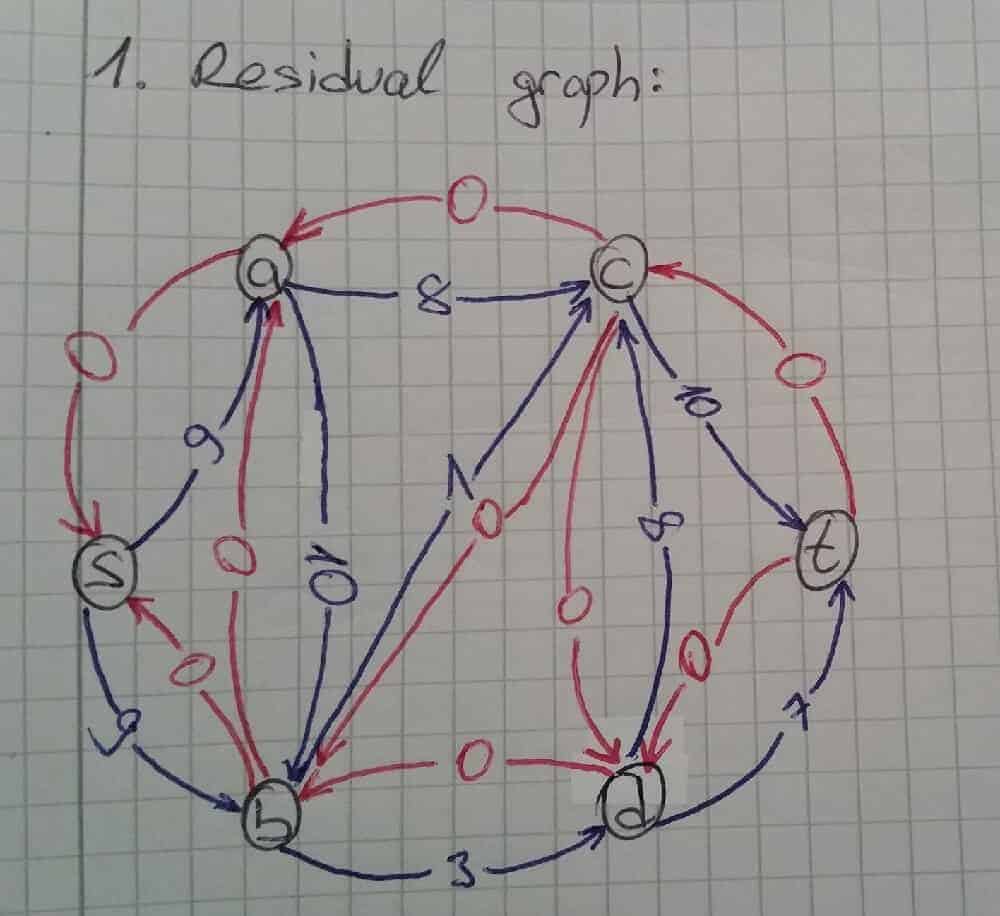
Residual graph belirlenirken güncel çizge baz alınır. Şuan ki güncel çizgede s-a kapasitesinin 9 birim olduğu ancak henüz bir akış olmadığı görülmektedir. Bu yüzden s-a yolunun kapasitesi 9-0 = 9 (kapasite – akan değer) birimdir ve herhangi bir akış olmadığı için a noktasından s noktasına dönüş yolu 0 birimdir. Aynı şekilde s noktasından b noktasına herhangi bir akış yoktur ve yolun kapasitesi 9 birimdir. Bu sebepten dolayı s noktasından b noktasına giden yolun değeri 9-0 = 9, b noktasından s noktasına dönen yolun değeri 0 birimdir. Aynı şekilde a-c yolu incelendiğinde yolun kapasitesinin 8 olduğu ve yol üzerinde bir akış olmadığı tespit edilir. Bu sebepten ötürü a-c değeri 8, c-a değeri 0 birimdir. Bu şekilde tüm noktaların gidiş ve dönüş değerleri belirlenir.
Residual graph oluşturulurken değeri 0 olan yolların çizilmesine gerek yoktur. İlk residual graph’ tan değeri 0 birim olan yollar çıkartılıp sadeleştirildiğinde aşağıdaki şekil ortaya çıkmaktadır.
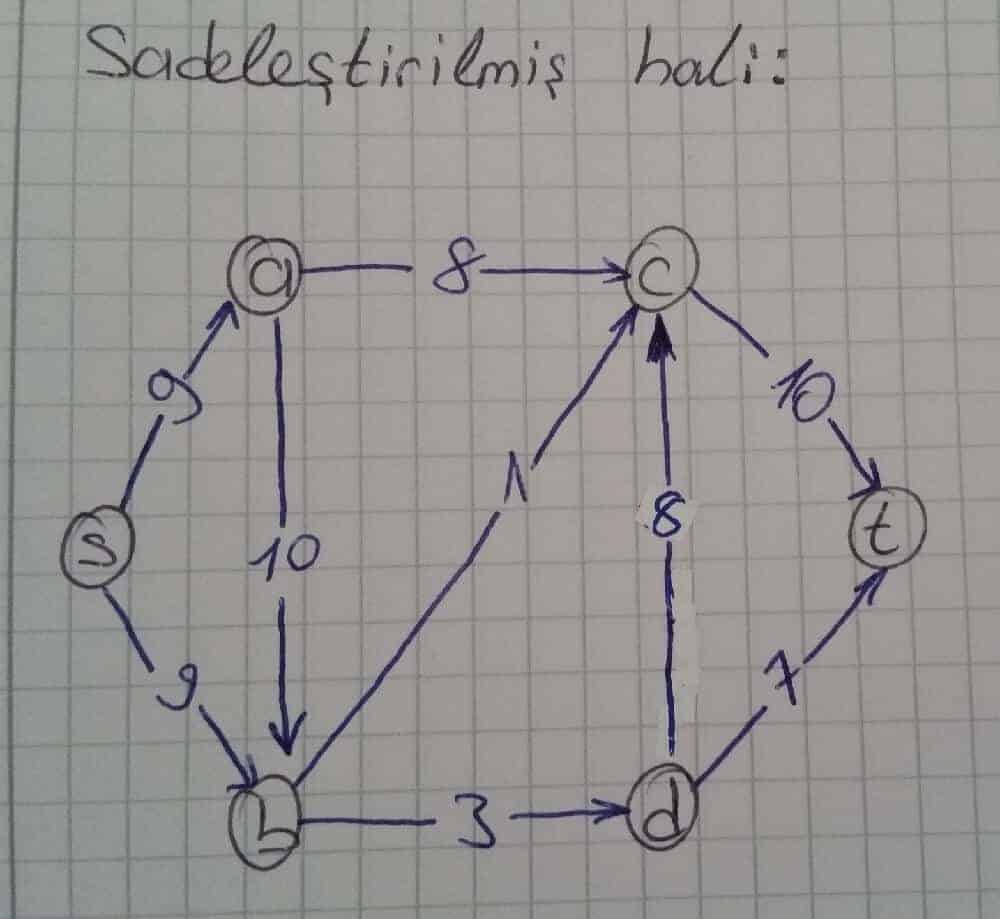
Algoritmanın bir sonraki adımında residual graph üzerinde, başlangıç noktasından bitiş noktasına ulaşan herhangi bir yol aranmaktadır. Bunu mümkün kılan birden fazla yol vardır. Bunlardan bazıları:
s→a→c→t
s→b→d→t
s→a→b→c→t
Bu yollardan herhangi birisi seçilir ve seçilen yolun maximum kapasitesi belirlenir. Seçilen bu yolun kapasitesi yol üzerindeki en düşük kapasiteye eşittir.
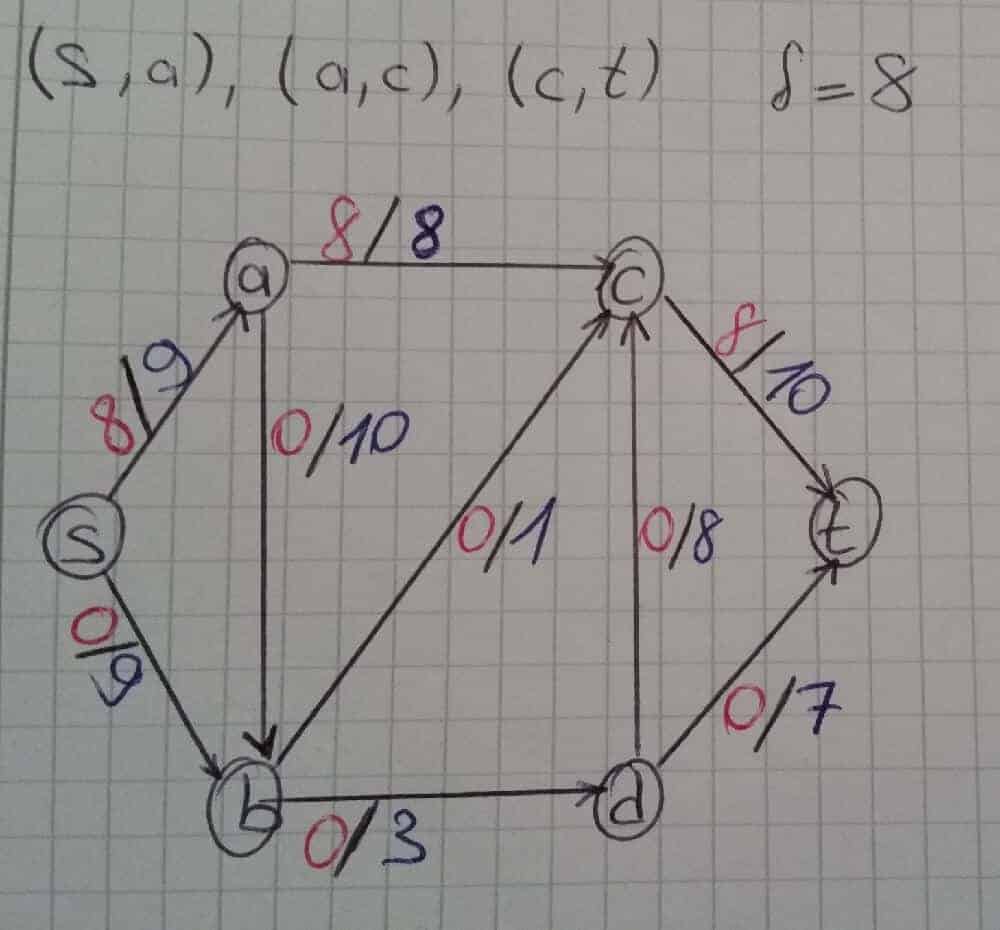
İlk olarak s→a→c→t yolu seçilsin. Bu yolun kapasitesi min{9, 8, 10} = 8 birimdir. Bir sonraki adımda başlangıç çizgesi yenilenir ve seçilen yoldaki akış değerleri güncellenir. Bir sonraki adıma geçmeden önce güncellenen çizgeye ait yeni bir residual graph oluşturulur.
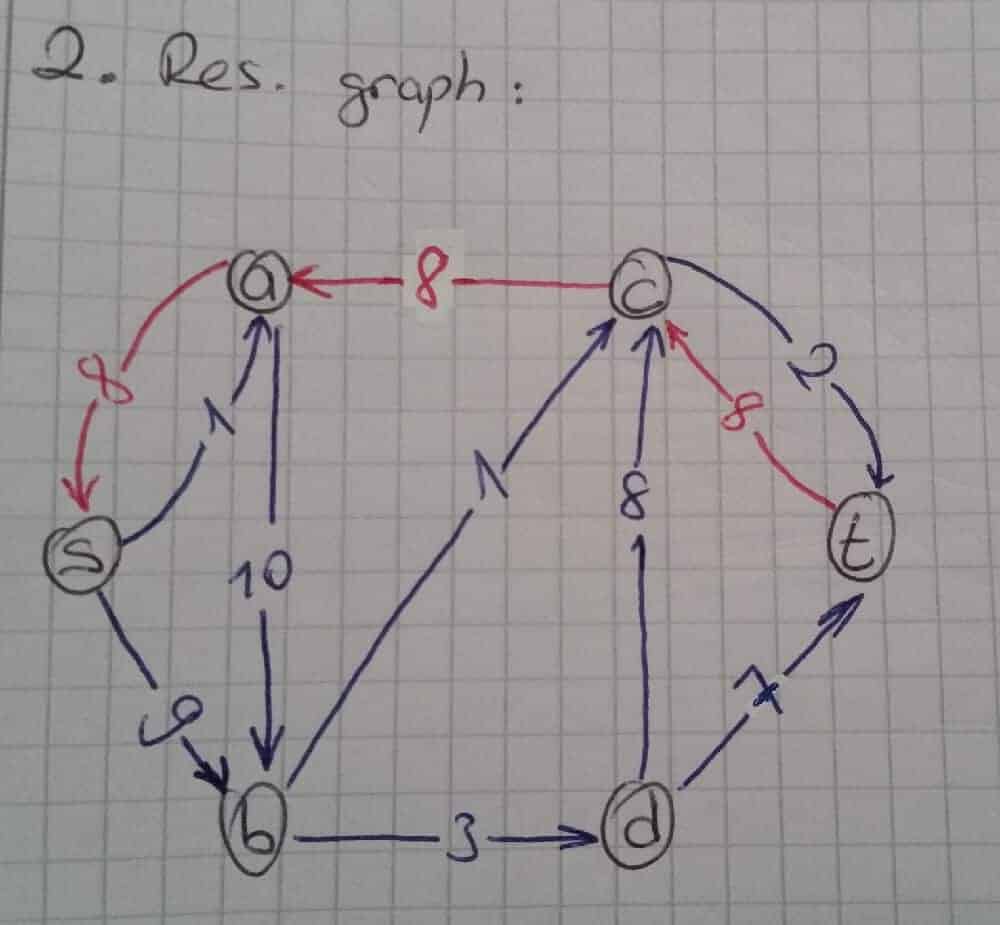
Oluşturulan çizgede s→a→c→t yoluna ait gidiş ve dönüş değerleri güncellenir. s-a yolunun kapasitesi 9 birimdi ve yol üzerinde herhangi bir akış yoktu. Bir önceki adımda bu yol üzerinden bitiş noktasına 8 birimlik bir akış sağlandı. Bu sebepten ötürü s-a yolunun yeni akış değeri 8, kapasite değeri ise 9-8 = 1 birim olmuştur. Aynı şekilde a-c ve c-t yollarının değerleride güncellenmelidir. Güncellenen çizgede bu yola 8 birimlik akış kazandırıldığı için residual graph’ ta a-c yolunun yeni kapasitesi 8-8 = 0 birim ve akış değeri 8 birimdir. Başlangıçta belirtildiği üzere değeri 0 birim olan yolun çizilmesi mecburi değildir. Bu yüzden sadece iki nokta arasındaki akış 8 birim olarak gösterilmiştir. Son olarak, güncellenen c-t yolunun yeni değerleri ise 10-8 = 2 birimlik kapasite ve 8 birimlik akıştır.
Algoritmaya göre oluşan yeni residual graph’ta başlangıç noktasından bitiş noktasına yeni yol aranır. Yeni bulunan yollar:
s→a→b→c→t
s→b→c→t
s→b→d→t
Bu yollar arasından tekrar birisi seçilir. Yeni seçilen yol s→b→d→t olsun.
Bu yolun maximum kapasitesi min{9, 3, 7} = 3 birimdir. Bir önceki güncel çizge tekrardan yenilenir, seçilen yol üzerinden 3 birimlik akış sağlanır ve oluşan bu yeni
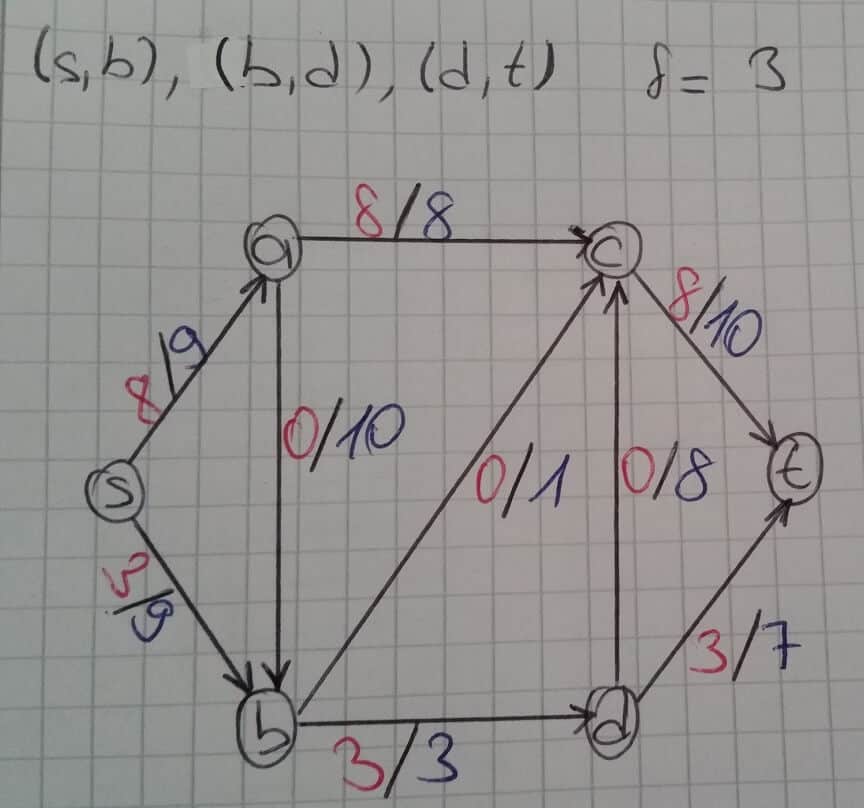
çizgeye ait residual graph çizilir.
Bir önceki residual graph’ ta olduğu gibi burada da seçilen yol üzerindeki kapasite ve akış değerleri yenilenir. s-b yolunun kapasitesi 9 birimdi ve herhangi bir akış yoktu. Çizgeye kazandırılan yeni akış sayesinde s-b yolunun yeni kapasite değeri 9-3 = 6 birim ve akış değeri 3 birim olarak geçilir. Aynı şekilde b-d yolu için hesaplanan yeni değerde kapasite 3-3 = 0 birim ve akış değeri 3 birim olarak bulunur. Son olarak d-t yolunun sahip olduğu 7 birimlik kapasite 7-3 = 4 birime düşer. Algoritma tekrardan güncel residual graph üzerinden yeni yol arar. Yeni bulunan iki farklı yol vardır. Bunlar
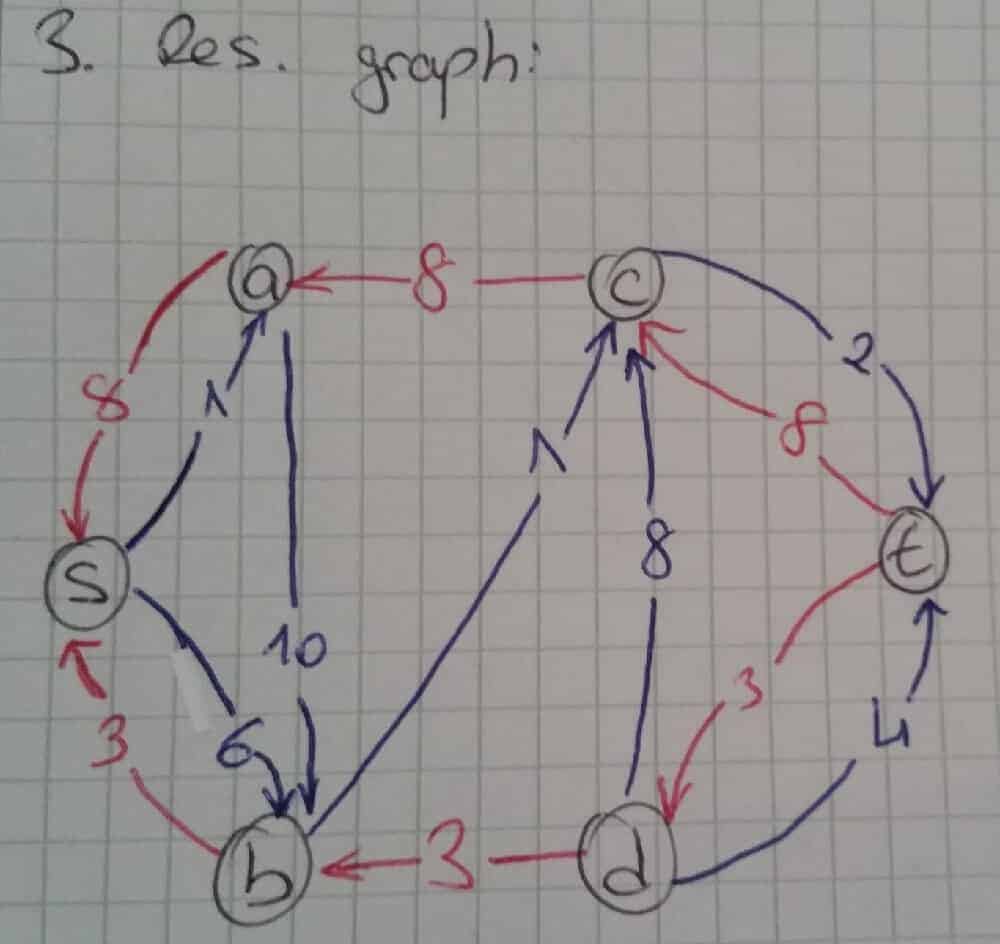
s→a→b→c→t
s→b→c→t
Yeni seçilen yol s→b→c→t olsun.
Son güncel residual graph’ tan bu yolun maximum kapasite değerinin min{6, 1, 2} = 1 birim olduğu görülür ve bu yol üzerinden fazladan 1 birimlik akış sağlanır. Güncellenen s-b yolunun yeni akış değeri 4, b-c yolunun 1 ve c-t yolunun ise 9 birimdir. Başlangıç noktasından bitiş noktasına yeni yol bulmak için tekrardan residual graph çizilir.
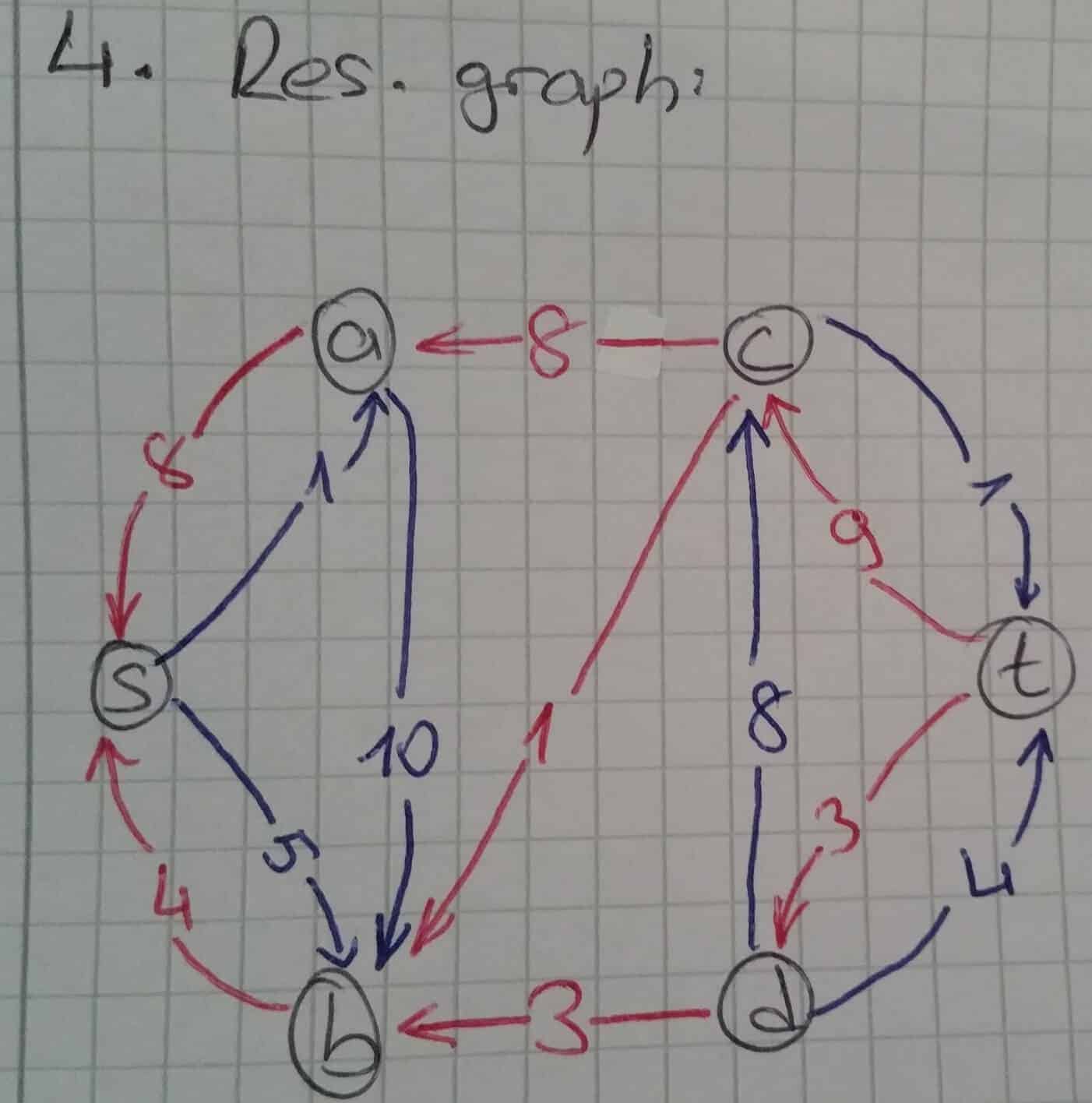
Yeni çizilen residual graph’ ta da akış ve kapasite değerleri güncellenir. 6 birimlik kapasiteye sahip olan s-b yolunun yeni kapasitesi 6-1 = 5 birime düşerken 3 birimlik olan akış değeri 3+1 = 4 birime yükselir. Aynı şekilde b-c yolunun yeni kapasite değeri 1-1 = 0 birim olurken akış değeri 0+1 = 1 birim olur ve son olarak c-t yolu 2-1 = 1 birimlik kapasite ve 8+1= 9 birimlik akış değerine sahip olur.
Yeni yol bulmak için son güncel residual graph incelendiğinde başlangıç noktasından sadece a ve b noktalarına ulaşılabildiği görülür. Bitiş noktasına ulaşılamadığı için algoritma tamamlanır.
Son olarak maximum akış değeri hesaplanır. Bu değer residual graphta başlangıç noktasına akan değerlerin toplamına yada bitiş noktasından çıkan değerler toplamına eşittir. s noktasına giren değerlerin toplamı 8+4 = 12 birim t noktasından çıkan değerlerin toplamı 9+3 = 12 birimdir. Yani s noktasında bulunan bir arıtma merkezinden t noktasına en fazla 12 birimlik su pompalanabilir.