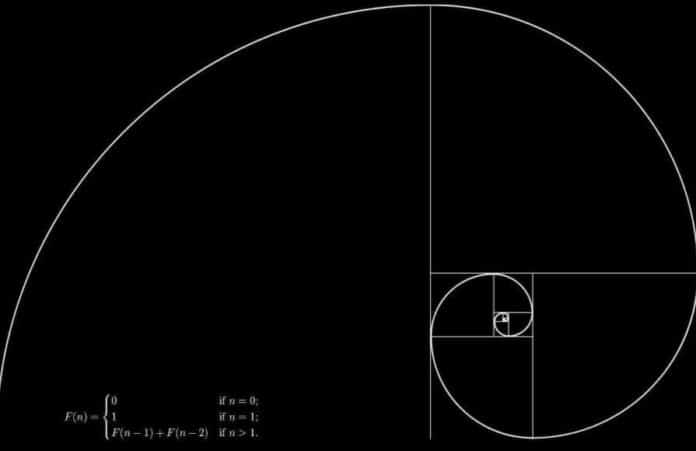
İdeal güzelliğin matematiği olarak karşımıza çıkan altın oran 1205 yılında İtalyan Matematikçi Leonardo Fibonacci “Liber Abaci” adlı kitabında tavşan problemi ile oluşan bir sabiti “Golden Ratio” olarak tanımlamıştır. Genel anlamda ilk tanım bu kitapta veriliyor olsa da M.Ö 3000’li yıllara kadar yapılmış yapılarda bu oranı görmek mümkün. Fibonacci serilerinin tanımı ile başlayalım.
Tanım: Fn olarak gösterilen bir dizide her terim kendinden önceki iki terimin toplamı ile oluşan dizilere Fibonacci dizisi denir. Bu dizide ilk iki terim F1=1 ve F2=1 olmak üzere iki sabit üzerine kurulmuştur.
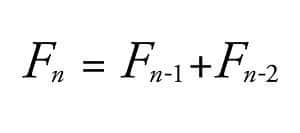
Dizinin terimleri: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
Fibonacci bu serinin her bir terimini evinde beslediği tavşanların çoğalmasına göre oluşturmuştur. Aldığı tavşanlar aylara göre ilk başta anlamsız bir şekilde çoğalıyor gibi görünmesine rağmen aslında arkasında esrarengiz bir matematik vardı.
Bu oluşan serinin terimlerinin birbirine oranı belirli bir müddet sonra (limiti) 1.618 sayısına yakınsıyordu. İlk başta anlam veremeyen Fibonacci bu sayının alınan herhangi bir doğrunun keyfi bir noktasından alınan sabitin oranlarıyla ilişkili olduğunu gözlemledi.
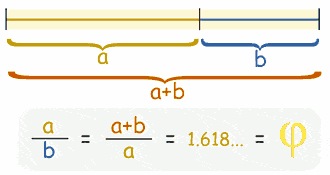
İşte bu noktada bu sayının hiç de hafife alınacak bir sayı olmadığı gözlemlenmiş oldu. Fibonacci bu eşitliğin 1.618 sayısına denk gelmesinden sonra “İlahi Oran” olarak tanımlamış daha sonraları bu sabitin en önemli savunucusu Leonardo Da Vinci “İlahi Oranın Yansımaları” adı altında birçok eser ortaya çıkarmıştır. 17. yüzyılda ise biraz daha matematik kokusu barındıran bir diskriminant köklerine sahip denklemin çözümleri tanımlandı ve bu çözümlerin altın oran sabitine eşit olduğu görüldü.
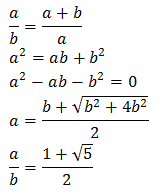
Yunan Alfabesinin 16. harfi olan phi harfi ile gösterilmektedir. Bugün kullanılan antik eserlerin birçoğunda, sanatçıların sanat eserlerinde bu matematiksel güzelliği görmekteyiz.
Fibonacci daha sonra bu dizedeki sayıları bir dikdörtgenin içine yerleştirmiş ve sarmal biçiminde alanlarına göre büyüdüğünü farketmiş bunu ise etrafındaki salyangoz kabuklarının tıpkı aynısı gibi olduğunu keşfetmiştir. “Altın Oran Spirali” olarak matematik tarihine geçen bu sarmal matematikçilerin güzellik olgusunu bir anda değiştirmiştir.
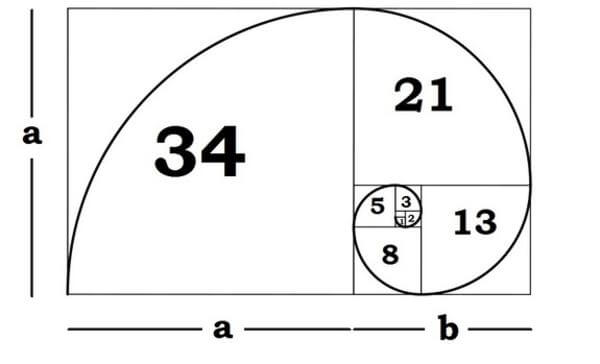
Bu spiral altın oran bahsedildiğinde aklımıza gelmesi gereken yapıdır. Yukarıda sözü edilen doğru parçasının bir dikdörtgen biçimine getirilmiş halidir. Uzun kenarı a+b, kısa kenarı ise a olan bir dikdörtgenin içerisindeki sarmal sadece Fibonacci dizisine göre yerleştirilebilir. Sizlerinde göreceği üzere uzun kenarın kısa kenara oranı burada 1.618 olacaktır.
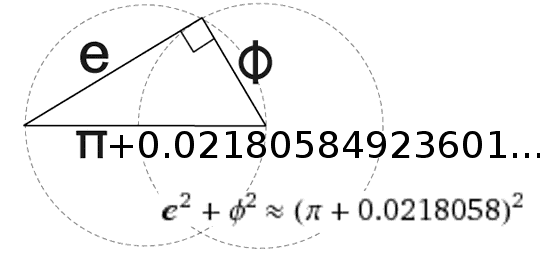
Bir dik üçgende e sayısı ile phi sayısı Pisagor teoreminin yardımı ile pi sayısının karesi ile yakından ilişkilidir. Bu matematiksel bağıntı matematik felsefesinin önemli sorularından bir tanesi olan “Matematik bir buluş mu yoksa icat mı?” sorusuna bir nebze cevap vermektedir.
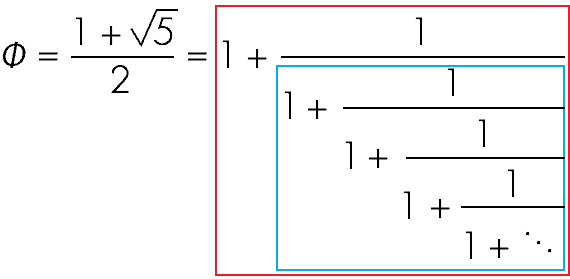
Matematiksel olarak phi sayısının açılımı sürekli kesirlerle de ilgilidir. Sürekli kesirlerin girdileri 1,1,1,1,… olarak alındığında bu sayı direkt olarak altın oran olarak bilinen 1.618 sayısına yakınsamaktadır.
Matematikçilere göre ideal güzelliğin matematiği olarak tasvir edilse de bu siz değerli okuyucuların insiyatifine kalmıştır.