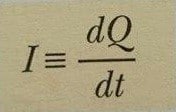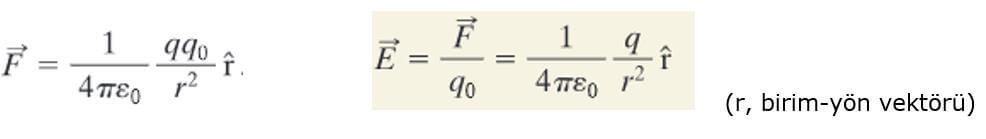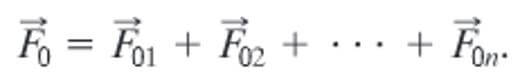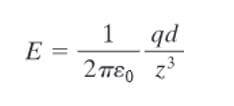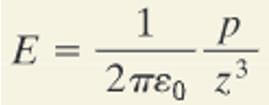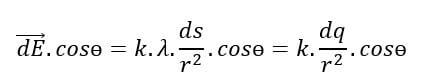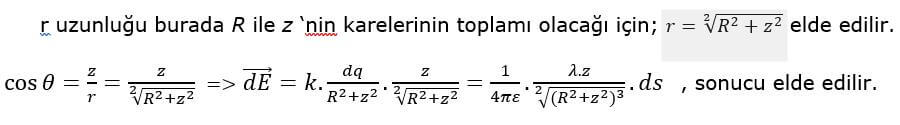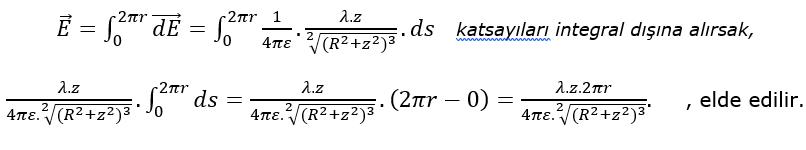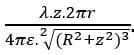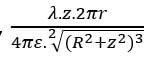Elektrik yükleri birbirlerine karşı itme ve çekme kuvveti uygularlar. En temelinde aynı cins yüklerin birbirini ittiğini, zıt yüklerin ise çektiğini biliyoruz. Yükler birbirilerine bu kuvvetleri nasıl uygular? Hatta bazı yükler aralarında çok uzak mesafeler olmasına rağmen birbirilerinden etkilenmektedir. Herhangi bir temas olmamasına rağmen biri diğerini nasıl etkiler? Cevabımız, Elektrik Alanı. Evet arkadaşlar belki birçoğumuz elektrik alanı terimini çok kez duyduk. Yükler arasındaki kuvvet bağıntısını açıklamak için ihtiyaç duyduğumuz bu terimin akıllarda daha anlaşılır olması için açıklamak istedik.
A ve B adını verdiğimiz iki yük düşünelim. A yükü, B yükünü etkileyebilmesi (herhangi bir kuvvet, hareket uygulayabilmesi) için B, A yükünün oluşturduğu elektrik alanı içerisinde olmalı, o alanın etki alanında bulunması gerekir. Bildiğimiz üzere bir yükün etrafında elektrik alan çizgileri vardır. Bulunduğu konum itibari ile kendi kapsama alanında başka bir yükü etkileyebilir. Özetle, yüklerin oluşturdukları elektrostatik kuvvet elektrik alan aracılığı ile ortaya çıkmaktadır.
Gauss yasası ile Newton’un kütle çekim yasası birbirlerine çok benzerlik gösterir aralarındaki fark ise kütle çekiminde kütleler birbirlerine sadece çekme kuvveti uygularken Gauss yasasında cisimler hem itme hem de çekme kuvveti uygulayabilirler. Birim zamanda hareket eden yük miktarına akım denilmektedir. (amper)
Yük birimi Coloumb olduğuna göre amper, coloumb/saniye öyleyse 1C=1A x 1 Sn olarak ifade edilir.
Milikan, yağ damlacıkları deneyinde elektronun yük miktarını bulduğu zaman maddeyi oluşturan temel yükün elektron olduğunu da kanıtlamıştır. Madde, kendisini oluşturan yapı taşlarından, temel birimlerden meydana gelmiştir. Temel yükten meydana gelen madde kesiklidir (kuantize) ve e– ‘nun n katı şeklinde ifade edilir. Temel yük, e– =1,602 x 10-19 C değerindedir. Parçacıklar da aslında birer maddedir. Ancak yükler, tıpkı kütle gibi maddenin bir özelliğidir.
Noktasal Yükün Elektrik Alanı
Şimdiye kadar bir yükün çevresinde elektrik alan oluşturduğunu ve bu alan aracılığı ile diğer yükler üzerinde elektrostatik kuvvet uyguladığını öğrenmiş olduk. Pozitif ya da negatif fark etmeksizin yükün uyguladığı kuvvet ve elektrik alan;
Kuvvet, yüklere ve aralarındaki mesafeye bağlı iken elektrik alan, yükün kendisine ve etki ettiği alanın mesafesine bağlıdır. Elektrik alanı q yükü kendisi oluşturur. q0 yükü q yükünün alanına dahilse bir F kuvveti doğar.
Bir test yükü birden fazla yük etkisinde kalırsa her bir yükün test yükü üzerinde oluşturduğu kuvvet hesaplanır ve süperpozisyon yöntemi ile toplanarak bulunur.
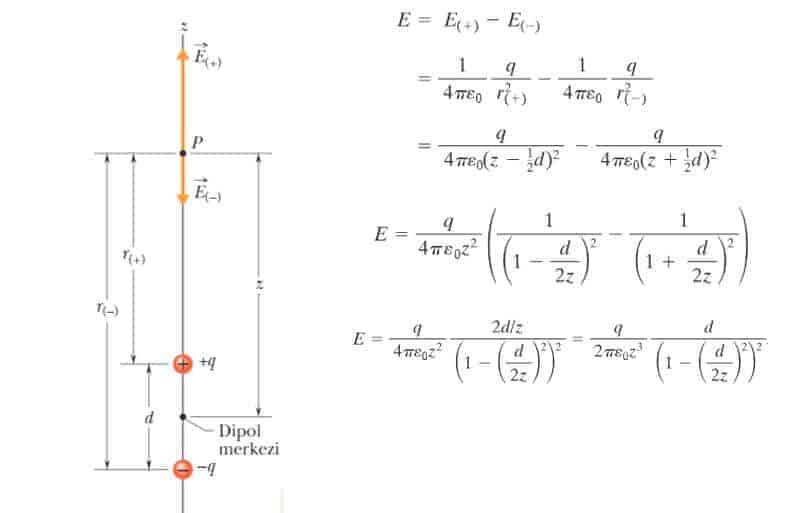
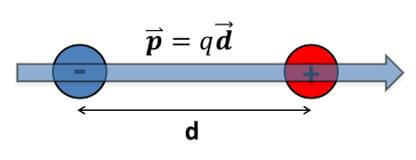
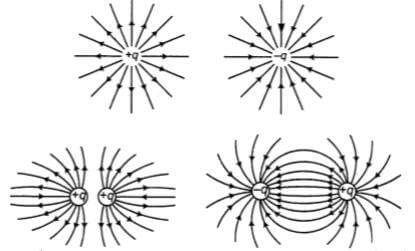
Birden fazla yük demişken elektrik dipolü kavramını tanımlamamız sonraki aşamalar için isabetli olacaktır. Elektrik dipolü; birbirilerine zıt aynı büyüklükteki yüklere denir. Örneğin aralarında d mesafesi olan +q ve -q yükü hayal edebiliriz.
Elektrik dipolleri, dipol merkezlerinden z mesafesindeki bir P noktasında elektrik alanı oluştururlar.
Çok uzaktaki bir z noktası için d mesafesi (z>>d) ihmal edilebilir. Öyleyse, şeklinde yazılır.
Elektrik dipollerinin momentleri ise dipol yüklerine ve aralarındaki mesafeye bağlıdır.
Elektrik dipol momentinin yönü ise negatif yükten pozitif yüke doğrudur ve p vektörü ile gösterilir. P vektörü ile dipolün konumunu kolaylıkla belirleyebiliriz.
Aynı elektrik alan ifadesini dipol momenti cinsinden ifade etmek istersek aşağıdaki gibi olur.
Yük Topluluklarının Elektrik Alanı: Çizgisel, Yüzey ve Hacim Yük Yoğunlukları
Çok miktardaki yükün elektrik alanını tek tek bulmak zor olacağı için yük yoğunluklarından istifade edilir. Bir yükün elektrik alanını bulabiliyorsak etrafındaki diğer yüklerin örneğin çizgisel bir hat üzerinde ya da bir yüzey üzerindeki yüklerin de elektrik alanını integral ile hesaplayabiliriz.
Hacim, alan ve uzunluk başına düşen yük miktarına sırasıyla; hacim yük yoğunluğu, alan yük yoğunluğu ve çizgisel yük yoğunluğu denir. Hesap edilecek yüzeye ve konuma göre kullanılacak yük yoğunluğu belirlenir. Örneğin, çok ince uzunlukta bir yüzeyde çizgisel yük yoğunluğunu ya da belirli bir et kalınlığına sahip dairinin hesabında yüzey yük yoğunluğu kullanabiliriz.
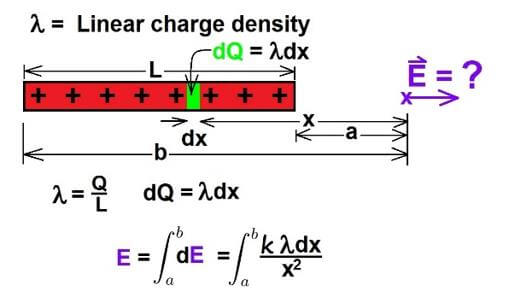
Yandaki şekilde görüldüğü gibi çizgisel hat üzerinde bulunan yüklerden çok küçük bir nokta için elektrik alanın bulunması yol boyunca toplam elektrik alanını bulmamızı sağlayacaktır. Seçmiş olduğumuz diferansiyel elemanın (yay parçası) yük miktarı; dq=dx.λ olacaktır. dx, diferansiyel parça uzunluğu ve çizgisel yük yoğunluğudur. Çarpımları diferansiyel parçanın toplam yük miktarını verir. Noktasal yükün elektrik alanı; ise çizgisel yüzeyin elektrik alanı B noktasından A noktasına kadarki yolun integrali alınarak bulunur.
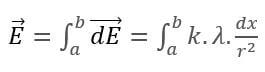olarak elde edilir. Aynı işlemi halka şeklindeki bir parça için yapmak istersek;
diferansiyel elemanın (yay parçası) yük miktarı; dq=ds.λ olacaktır.
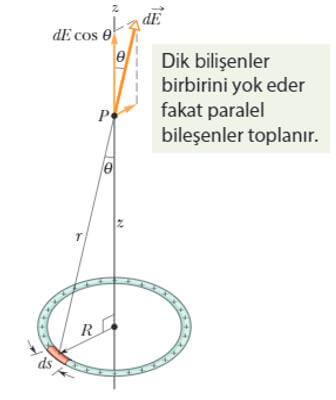
dS elemanın P noktasındaki elektrik alanı belirli bir açıya sahip ve yatay-dikey bileşenleri mevcuttur. Yatay bileşenler halkadaki tüm elemanlar için aynı yönde olmayacağı için birbirilerini sönümlerler. dS’nin karşısında dS’ adında başka bir diferansiyel parça aldığımız zaman bu kez yatay bileşen batı yönünde olacaktır. dS nin yatay bileşeni ise doğu yönündedir. Halkanın 180°’lik dilimi için yatay bileşenler doğu diğer 180°’lik dilimi için batı yönünde olacağı için elektrik alan hesabında dE’nin dikey bileşenini kullanmamız yeterli olacaktır.
Halkadaki toplam elektrik alan ise;
Sonuç olarak halkanın P noktasındaki meydana getirdiği elektrik alanını aşağıdaki gibi bulduk. Peki çok uzaktaki başka bir nokta için halkanın elektrik alanını bulmak isteseydik; z=∞ ya da z≫R için R değeri ihmal edilebilir ve bağıntımız,
ifadesi aslında halkadaki toplam yükü verdiği için bu kısma “q” denilebilir. Ve z’ler birbirini götürürse; q/(4πε.z^2 ), halka merkezinden çok uzaktaki bir noktada oluşan elektrik alanı verir.
q/(4πε.z^2 ) elde edilen bu ifadeyi daha öncesinden noktasal yükün elektrik alanı olarak bulmuştuk. Buradan anlaşılan çok uzaktaki bir noktadaki elektrik alan büyüklüğü ile noktasal yükün elektrik alan büyüklüğü aynıdır. Açıklaması ise halkaya çok uzaktan bakıldığında zaten bir nokta gibi görüneceği için oluşturduğu elektrik alan da noktasal elektrik alanın büyüklüğü ile aynı büyüklüktedir.
Eğer bu P noktasını halka merkezinde seçmiş olsaydık sonuç nasıl değişirdi bir de ona bakalım. Halka merkezindeki nokta için, olacaktır. Öyleyse
payda kısmı 0 olacak ve sonuç E ⃗=0 olacaktır. Formül üzerinde 0 değerini görsek de bunun açıklaması merkezdeki noktaya halka üzerinde eşit büyüklükte bir elektrik alan etki edecektir ve net elektrik alan büyüklüğü sıfır olmuş olur.
Stay with science!