Elektrik Alan Konu Anlatımı

Bu yazımızda elektrik alan konu anlatımı yapacağız ve elektrik alan soruları çözeceğiz, bunun yanı sıra dipol elektik alan konusuna değineceğiz. Şimdiye dek kütle çekim kuvveti ve elektrik kuvveti olmak üzere, tartışmalarda iki alan kuvveti tanıttık. Bundan önce değinildiği üzere, alan kuvvetleri, uzayda cisimler birbirlerine fiziksel olarak değmeseler bile etkileşebilirler. Uzayda bir noktadaki, g kütle-çekim alanının, m deneme kütlesine etkiyen F , kütle çekim kuvvetinin, deneme kütlesine bölümüne eşit olduğu tanımlanmıştı: g = F_g/m. Elektrik kuvvetlerine benzer bir yaklaşım Michael Faraday tarafından yapılmıştır. Bunun pratik önemi nedeniyle gelecek birkaç bölümde de değinilmiştir. Bu yaklaşımda elektrik yüklü bir cismi saran uzay bölgesinde elektrik alanının bulunduğu söylenir. Bu alana başka bir yüklü cisim girdiğinde buna bir elektrik kuvveti etkir. Örneğin, küçük bir artı q₀ deneme yükünün daha büyük artı yük taşıyan ikinci bir cismin yakınında bulunduğu Şekil 1 da göz önüne alınsın. Deneme yükünün konumundaki elektrik alanın şiddeti (başka deyişle büyüklüğü) birim yük başına elektrik kuvveti olarak tanımlanır. Daha kesin bir anlatımla,uzayda bir noktadaki E elektrik alanı, o noktaya konulan artı bir deneme yüküne etkiyen Fe elektrik kuvvetinin deneme yükünün q0 büyüklüğüne bölümü olarak tanımlanır:

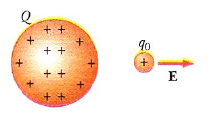
Şekil 1 Çok daha büyük artı Q yükü taşıyan bir cismin yakınına konulmuş küçük bir artı q₀ deneme yüküne gösterilen doğrultuda bir E elektrik alanı etkir.

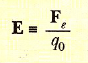
E, deneme yükünce oluşturulmayıp deneme yüküne dışarıdan etkiyen bir alandır. Ayrıca elektrik alanının varoluşu, kaynağının bir özelliğidir. Örneğin, her elektronla birlikte kendi alanı da vardır.

E vektörünün SI sistemindeki birimi coulomb başına newtondur (N/C) ve Şekil 1’deki gibi doğrultusu, alana konulan artı bir deneme yüküne etkiyen kuvvetin doğrultusudur. F nin artı bir deneme yüküne etkidiğini varsaydığımızdan E, F doğrultusundadır. Buna göre, durgun bir deneme yükü bir noktaya konulduğunda elektrik kuvvet etkisinde kalırsa, o noktada bir elektrik alanı vardır denir. Bir noktadaki elektrik alanın doğrultu ve büyüklüğü bir kez bilindikten sonra, o noktaya konulan yüklü herhangi bir parçacığa etkiyen kuvvet Eşitlik 1’den hesaplanabilir. Bunun yanında, bir noktada deneme yükün bulunup bulunmadığına bakılmaksızın (boş uzayda bile) o noktada elektrik alanının bulunduğu söylenir. (Bu, bir cismin oluşturduğu kütle-çekim alanına benzerdir. Bu alanın o noktada, alanı algılaması için başka bir cismin bulunup bulunmamasına bakılmaksızın, var olduğu söylenir.) Çeşitli kaynakların elektrik alan büyüklükleri Tablo 1’de verilmiştir.

Eş. (1) kullanılırken, q₀ deneme yükünün elektrik alanı oluşturan yük dağılımını bozmayacak kadar küçük olduğu varsayılır. Şekil 2a daki gibi düzgün yüklü bir metal küre yakınına son derece küçük bir q₀ deneme yükü konulduğunda, elektrik alanını oluşturan metal küredeki yük düzgün dağılımını korur. Deneme yükü Şekil 2b deki gibi yeterince büyük olduğunda (q’₀>>q₀), metal küredeki yük, yeni bir düzenlemeye uğrar ve kuvvetin deneme yüküne oranı farklı olur: (F’e/q’₀ ≠ Fe/q₀). Bu durumda, metal küredeki bu yük dağılımının yeniden düzenlenişi nedeniyle, oluşturduğu elektrik alanı, çok daha küçük q₀ bulunması durumunda oluşturulan alanlardan farklıdır.

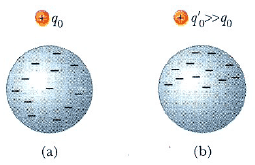
Bir elektrik alanının doğrultusunu belirlemek için Şekil 3’deki gibi bir P noktasındaki bir q₀ deneme yükünden r uzaklığında bulunan bir q nokta yükünü ele alalım. Coulomb yasasına göre q yükünün deneme yüküne uyguladığı kuvvet;

dir. Burada r (şapkalı) , q dan q₀ ‘a yönelik birim vektördür. Deneme yükünün bulunduğu konumda elektrik alanı E = Fe/q₀ ile tanımlandığından, q nun P de oluşturduğu elektrik alanı:

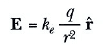
dir. Şekil 3a daki gibi, q artı ise, alan, bu yükten yarıçap boyunca dışarı doğru yönelmiştir. Şekil 3b deki gibi q eksi ise, alan, yüke doğru yöneliktir.

Nokta yükler topluluğundan ileri gelen elektrik alanını hesaplamak için, Eş. 2 kullanılarak P noktasındaki elektrik alan vektörleri tek tek bulunup vektörel olarak toplanır. Başka bir deyişle, yükler topluluğunun herhangi bir P noktasında oluşturduğu toplam elektrik alanı, bütün yüklerin elektrik alanlarının vektörel toplamına eşittir.

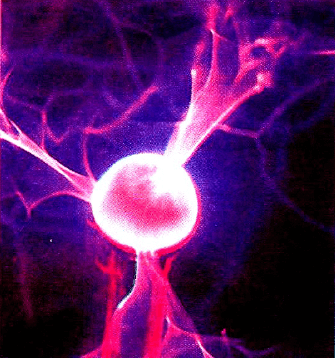
Şekli 4:Bir üreteçle yüklenen bu metal küre net bir elektrik yükü taşımaktadır. Küredeki yük yoğunluğu, çevresinde şiddetli elektrik alanı oluşturur. Böylece yükler küreyi saran gazdan kaçarak pembe ışıklamaya yol açarlar. (E.R. Deggjiner/H. Arrmtrong Roberts)

Alanlara uygulanan bu üstüste binme ilkesi, elektrik kuvvetlerinin üst üste binme özelliğinin doğal bir sonucudur. Buna göre, yükler topluluğunun elektrik alanı

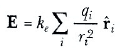
şeklinde belirtilebilir. Burada,r_i, i inci q_i yükünden P noktasına (deneme yükünün bulunduğu yer) olan uzaklık ve r_i(şapkalı), q_i: den P ye yönelmiş bir birim vektördür.

Elektrik Alan Soruları ve Çözümleri

Örnek1: Bir q₁ = 7,0 μC yüklü başlangıç noktasında, ikinci bir q₂ = -5,0 μC yükü x ekseni üzerinde başlangıçtan 0,3 m uzakta bulunmakladır (Şekil 5). (0, 0,40) m koordinatlı P noktasındaki elektrik alanını bulunuz.

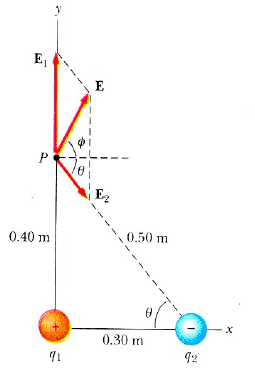
Şekil 5: P deki E toplam elektrik alanı E₁ + E₂ vektör toplamına eşittir. Burada E₁ ,q₁ artı yükünden, E₂, ise eksi q₂ yükünden ileri gelen alanlardır.
Çözüm: Önce, her bir elektrik yükünden ileri gelen elektrik alanlarının büyüklüklerini bulalım. Pnoktasuıdaki 7,0 yükünden ileri gelen E₁ ve -5,0 μС yükünden ileri gelen E₂ alanları Şekil 5 te gösterilmiştir. Bunların büyüklükleri

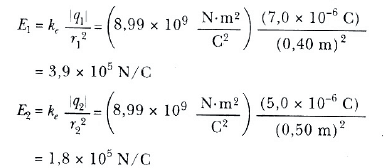
E₁, vektörünün yalnız у bileşeni vardır. E₂; vektörünün cosθ = (3/5)E₂ verilen x bileşeni, -E₂sinθ = (-4/5)E₂, ile verilen eksi у bileşeni bulunmaktadır. Böylece vektörleri,

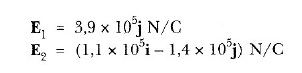
şeklinde ifade edilebilir. P deki E bileşke alanı, E₁ ve E₂ nin üstüste binmesiyle oluşur:

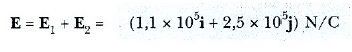
Bu sonuçtan, E nin 2,7 х 10⁵ N/C büyüklüğünde ve artı x ekseniyle 66° lik Φ açısı yaptığı bulunur.

Örnek2: Bir elektrik dipolü, aralarında belli bir uzaklık bulunan artı ve eksi -q yük çiftinden oluşur. Şekil 6 deki dipol için P noktasında bu yüklerin oluşturduğu E elektrik alanını bulunuz. Burada P, başlangıç noktasından y>>a uzaklığındadır.

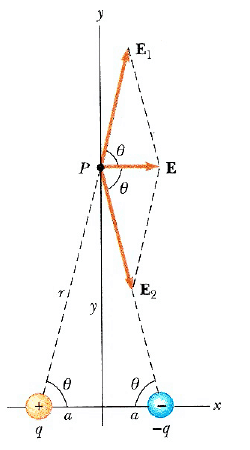
Çözüm: P noktası yüklerden aynı uzaklıkla bulunduğundan, bu noktada bu iki yükün oluşturduğu E₁ ve E₂ alanlarının büyüklükleri eşittir. Toplam alan E = E₁ + E₂ olup burada:

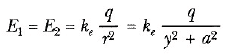
dir. E₁ ve E₂ nin у bileşenleri birbirini yok ederler, x bileşenleri ise artı x yönünde olup birbirlerine eşittir. Bunun sonucu olarak E, x eksenine paralel olup 2E₁cosθ büyüklüğündedir. Şekil 6 dan cosθ = a/r= a/ (y² + a²)^1/2 olduğu görülür. Bu nedenle

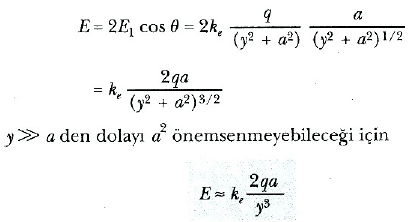
yazılabilir.

Böylece, iki yükü birleştiren doğru parçasının orta dikmesi üzerinde uzak noktalarda dipolün oluşturduğu elektrik alanının 1/r³ le değiştiği, oysa bir nokta yükün alanının 1/r2 ile daha yavaş değiştiği görülür. (Bakınız Eşitlik 3) Bunun nedeni, uzak noktalarda eşit büyüklükte zıt iki yükün alanlarının birbirlerini hemen hemen yok etmeleridir. Çift kutuplunun (dipolün) E alanının 1/r³ değişimi, x ekseni üzerindeki veya herhangi genel konumdaki uzak bir nokta için de elde edilebilir.

Dipol, Hidroklorik asit (HCI) gibi birçok molekül için iyi bir modeldir. Nötr atom ve moleküllerin bir elektrik alanı içine konulduklarında dipol (çiftkutuplu) gibi davrandıkları, sonraki yazılarımızda görülecektir. Bundan başka, HCI gibi birçok molekül kalıcı çiftkutupludur. Böyle çiftkutupluların elektrik alanına konulan maddelerin davranışları üzerindeki etkisi, ilerideki konularımız da incelenecektir.