Düzgün Olmayan Dairesel Hareket Konu Anlatımı

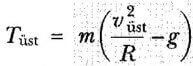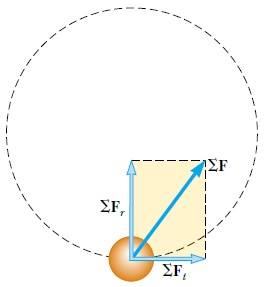
Merhaba arkadaşlar bu yazımızda sizlere düzgün olmayan dairesel hareket konusunu anlatacağız, bunun yanı sıra sizlere konuyu daha iyi kavramanız için düzgün olmayan dairesel hareket ile ilgili örnekler çözeceğiz. Dairesel bir yörüngede süratini değişerek hareket eden parçacı­ğın, merkezcil ivmesinin yanında, dv/dt büyüklüğünde bir teğetsel ivmesinin de olduğunu bulmuştuk. Böylece parçacığa etki eden kuvvetin hem merkezcil hem teğetsel bileşeni olmalıdır. Yani, toplam ivme a = a_r + a_t olduğundan,  parçacığa etki eden toplam kuvvet F = F_r + F_t ile verilir ve Şekil 1 de göste­rildiği gibidir.

Bu kuvvetin F_t vektör bileşeni, dairenin merkezine yönelmiştir ve merkezcil ivmenin meydana gelişinden sorumludur. Kuvvetin F_t vektör bi­leşeni yörüngeye teğettir ve teğetsel ivmenin meydana gelişinden sorumludur ve parçacığın hızının zamanla değişmesine sebep olur. Aşağıdaki örnek bu tip hareketi açıkça anlatmaktadır.

Şekil 1 de Parçacığa etkiyen kuvvetin yörüngeye teğet bileşeni, ∑F_t hızın büyüklüğünü değiştirir. Bu durumda, parçacığa uygulanan toplam kuvvet, teğet doğrultusundaki ve yarıçap doğrultusundaki kuvvetlerin vektörel toplamıdır, yani ∑F =∑F_t + ∑F_r

Düzgün Olmayan Dairesel Hareket Örneği

m kütleli küçük bir küre Şekil 2a da görüldüğü gibi, R uzunluğunda bir ipin ucuna bağlanarak düşey düzlemde bir O noktası etrafında dairesel yörüngede döndürülüyor. Cismin hızının v olduğu ve ipin düşeyle θ açısı yaptığı bir anda, ipteki gerilmeyi hesaplayınız.

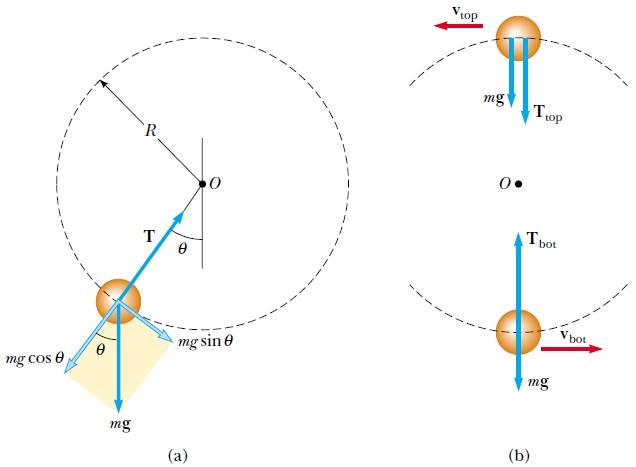
Çözüm: Öncelikle hızın düzgün olmadığına dikkat etmeliyiz. Ağırlığın teğet bileşeni, teğetsel ivmeyi oluştur­muştur. Şekil 2b deki serbest cisim çizeneğinden de gö­rüldüğü gibi, cisme uygulanan kuvvetler F_g = mg ağırlığı ve ipteki T gerilmesidir. mg nin teğetsel bileşeni mgsinθ  ve yarıçap doğrultusundaki bileşeni mgcosθ dır. Newton’un 2. hareket yasası

∑F_t= mgsinθ = ma_t

a_t = gsinθ

bulunur. İvmenin bu bileşeni v hızının zamanla değiştiği­ni ifade eder. Çünkü a_t = dv/ dt dir.

Newton’un ikinci yasasını yarıçap doğrultusunda uygu­larız. T ve a_r nin yarıçap doğrultusunda olduğuna dikkat ederek

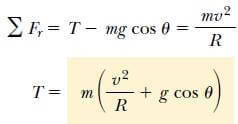
bulunur.

Özel Durumlar Yörüngenin en üst noktasında θ = 180° dir. cos 180° = -1 olduğundan üst nokta için T_üst elde edi­lir

Bu değer, T gerilmesinin minimum değeridir. Tam bu noktada a_t teğetsel ivme mevcut olmaz, a_t = 0 olur. Sadece a_r yarıçap doğrultusundaki ivme mevcut olur. Bu ivmenin yönü aşağı doğrudur.

Yörüngenin en alt noktasında  θ =0° dir, ve cosθ = 1 dir. Buradan T_alt bulunur:

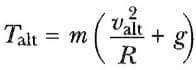olur. Bu değer de T gerilmesinin maksimum değeridir. Tekrar bu noktada a_t = 0 dır. Sadece yarıçap doğrultusun­da yukarı yönlü ivme mevcuttur.

Bu yazımızda sizlere düzgün olmayan dairesel hareket konusunu anlattık. Bu yazımız şle bağıntılı olan newtonun hareket konunlarına göz atmayı unutmayınız.