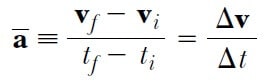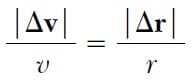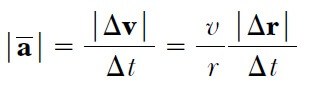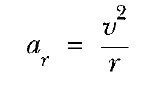Merhaba arkadaşlar bu yazımızda sizlere düzgün dairel hareket konusunu anlatacağız.Şekil 1a, sabit v sürati ile dairesel yolda hareket eden bir arabayı göstermektedir. Böyle bir harekete düzgün dairesel hareket denir. Arabanın hareket doğrultusu değiştiğinden, arabanın bir ivmesi vardır. Herhangi bir hareket için hız vektörü yola teğettir. Sonuç olarak bir cisim dairesel bir yolda hareket ettiği zaman, hız vektörü dairenin yarıçapına dik olur.
Düzgün Dairesel Hareket Formülleri
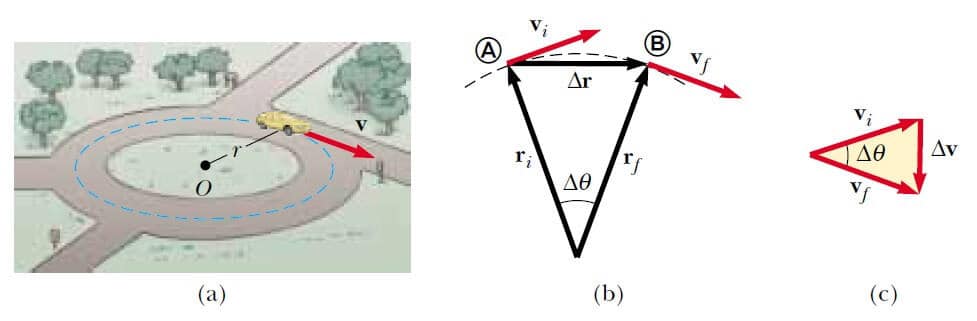
Şekil 1 (a) Sabit büyüklükde hızla dairesel bir yol boyunca hareket eden bir araba düzgün dairesel hareket yapar, (b) Parçacık A dan B ye hareket ederken, hız vektörünün doğrultusu vi den vf ye değişir, (c) Küçük Δr için dairenin merkezine doğru olan, hızdaki Δv değişiminin çizimle gösterilmesi.
dairenin merkezine yöneldiğini göstereceğiz. Bu tür ivmeye merkezcil ivme denir ve büyüklüğü
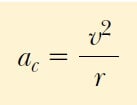
ile verilir. Burada r dairenin yarıçapıdır ve ar merkezcil ivmenin radyal doğrultuda olduğunu göstermek için kullanılır.
1 Eşitliğini elde etmek için, önce parçacığın A noktasında ve sonra B noktasında olduğunu gösteren 1b şeklini ele alalım. Burada cisim önce ti zamanında vi, hızıyla A noktasında ve sonra tf zamanında vf hızıyla B noktasında görülmektedir. vi ve vf ’nin sadece doğrultularının farklı olduğunu da kabul ediyoruz. Büyüklükleri (yani, vi – vf = v) aynıdır. Parçacığın ivmesini hesaplamak için işe, ortalama ivmenin tanımıyla başlayalım:
Bu eşitlik vi ’yi vf ’den vektörel olarak çıkartmamız gerektiğini söyler. Burada Δv = vf- vi hızdaki değişimdir, vi + Δv = vf olduğundan, Şekil 1c ’deki vektör üçgenini kullanarak, Δv vektörünü bulabiliriz.
Şimdi kenarlan Δr ve rolan Şekil 1b ’deki üçgeni göz önüne alalım. Bu üçgen, Şekil 1c ’deki kenarları Δv ve v olan üçgene benzerdir. Bu özellik, kenarların uzunlukları arasında aşağıdaki gibi bir bağıntı yazabilmemize olanak verir:
Bu eşitlik Δv için çözülebilir ve elde edilen ifade
Şimdi Şekil 1b ’deki A ve B noktalarının birbirine son derece yakın olduğunu düşünelim. Bu durumda, Δv dairesel yolun merkezine doğru yönelecek ve ivme de, Δv doğrultusunda olduğundan, merkeze doğru yönelecektir. Ayrıca, A ve B noktası birbirine yaklaşırken, Δt sıfıra ve Δr/Δt oranı da v süratine yaklaşır. O halde, Δt —> 0 limitinde ivmenin büyüklüğü
olur. Boylere düzgün dairesel harekette, ivmenin dairenin merkezine doğru yöneldiği ve büyüklüğünün v/r olduğu sonucunu çıkarırız. Burada v parçacığın sürati ve r dairenin yarıçapıdır. ar ’nin boyutlarının L /T2 olduğunu gösterebilmelisiniz. Bu yazımızda sizlere düzgün dairesel hareket konusunu anlattık. Diğer yazımızda görüşmek üzere.