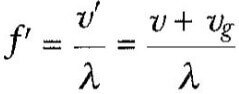Doppler Olayı Nedir

Merhaba arkadaşlar bu yazımızda doppler olayı, doppler olayı formülü ve matematiksel çözümlenmesini sizlere anlatacağım. Muhtemelen, bir araç sizi geçerken aracın korna sesinin nasıl değiştiğine dik­kat etmişsinizdir. Bir otomobil veya kamyon, kornasını çalarak hareket eder­ken duyduğunuz sesin frekansı, araç size yaklaşırken daha yüksek, uzaklaşır­ken daha düşüktür. Bu, Doppler olayına bir örnektir.

Açıkça fark edilen bu frekans değişiminin nasıl olduğunu anlamak için, dal­galarının T = 3s periyodla, hafif dalgalı denizde demirli olan bir botta olduğu­nuzu düşünün. Bu, her 3s de bir dalga tepesinin botunuza çarptığını ifade eder. Şekil 1a, su dalgaları sola doğru hareket ederken bu durumu gösteri­yor. Eğer, bir tepenin çarpması anında saatinizi t=0 ’a ayarlarsanız, bir çarpma olduğu zaman saatiniz 3s’yi, üçüncü çarpma olduğu zaman 6s’yi gösterir v.s. Bu gözlemlerden dalga frekansının f=1/T= (1/3) Hz olduğu sunucunu çıkarırız. Şimdi motorunuzu çalıştırdığımızı ve Şekil 1b de görüldüğü gibi gelen dal­galara doğru gittiğinizi farz ediniz. Yine saatinizi, bir tepe, botunuzun önüne çarparken t=0’a ayarlayın. Şimdi, böylece; siz yeni bir dalga tepesine doğru ha­reket ederken, o da size doğru hareket eder. Dalga tepesi ilk çarpmadan sonra 3s ’den daha az bir zamanda size çarpar. Başka bir deyişle, sizin gözlediğiniz pe­riyot, hareketsiz iken gözlediğiniz periyottan daha kısadır. Çünkü gözlediğimiz frekans f= 1/T hareketsiz olduğunuz haldekinden daha büyüktür.

Geri döner, dalgalarla aynı yönde hareket ederseniz (Şekil 1c de görü­lüyor), ters etki gözlersiniz. Bir tepe botun arkasına çarparken saatinizi t = 0’a ayarlıyorsunuz. Şimdi gelecek tepeden uzaklaştığınızdan dolayı, tepenin size ulaşması için geçen zaman, saatinizin sahip olduğu zamandan daha fazladır. Böylece, hareketsiz olduğunuz zamankinden daha düşük bir frekans ölçersi­niz.

Bu etkiler olur, çünkü botunuz ve dalgalar arasındaki bağıl hız, botunu­zun hızı ile hareket doğrultusuna bağlıdır. Şekil 1b de sağa doğru hareket ettiğiniz zaman bu bağıl hız dalga hızından daha büyüktür. Bu durum frekan­sın artmasına yol açar. Döndüğünüz ve sola doğru hareket ettiğimiz zaman su dalgalarının frekansında gözlendiği gibi, bağıl hız daha düşük olur.

Doppler Olayı Formülü

Şimdi, benzer bir durumu ses dalgaları ile inceleyelim. Burada su dalgala­rı ses dalgalarına karşılık gelir; su hava yerine geçer ve bottaki adam sesi din­leyen gözlemci olur. Bu durumda, gözlemci hareket eder, S ses kaynağı dur­gundur. Basitlik için, havanın hareketsiz olduğunu ve gözlemcinin kaynağa doğru hareket ettiğini kabul ediyoruz. Gözlemci, hareketsiz nokta kaynağa doğru v hızı ile hareket ediyor (v_k = 0) (Şekil 2). Genel olarak durgun ol­maktan, ortama göre (havaya) hareketsiz olmayı kastediyoruz.

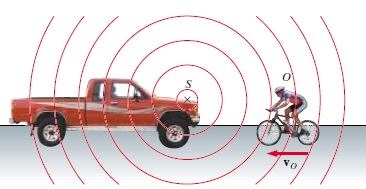
Kaynağın frekansını f, dalga boyunu λ ve sesin hızını v olarak alacağız. Gözlemci de hareketsiz olsaydı, açıkça saniyede f dalga cephesi duyacaktı. (Ya­ni; v_g = 0 ve v_k = 0 olduğu zaman, ölçülen frekans kaynak frekansına eşit olurdu). Gözlemci kaynağa doğru hareket ettiği zaman, gözlemciye göre dalgala­rın hızı v’ = v + v_g olur, bot halindeki gibi; fakat λ dalga boyu değişmez. Bu ne­denle, v = λf, kullanarak gözlemci tarafından işitilen frekansın art­tığını söyleyebiliriz. Bu frekans,

ile verilir. λ = v/f olduğundan f‘

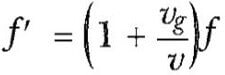
şeklinde ifade edilebilir.

Gözlemci kaynaktan uzaklaşıyorsa, gözlemciye göre dalganın hızı v’ = v – V_g olur. Bu durumda gözlemci tarafından duyulan frekans azalmıştır ve aşağıdaki eşitlikle verilir:

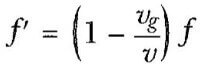
Genel olarak, gözlemci, durgun kaynağa göre v hızı ile hareket ediyorsa, gözlemci tarafından duyulan sesin frekansı

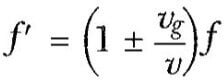
olur. Burada pozitif işaret, gözlemci kaynağa doğru hareket ettiği zaman, ne­gatif işaret de gözlemci kaynaktan uzaklaştığı zaman kullanılır.

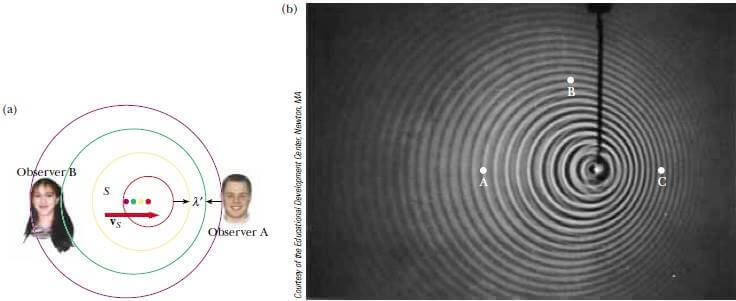
Şimdi, kaynağın hareketli, gözlemcinin hareketsiz olduğu durumu incele­yelim. Kaynak, Şekil 3a’daki gibi, A gözlemcisine doğru hareket ederse; gözlemci tarafından algılanan dalga cepheleri, ilerleyen dalga yönündeki dal­ga kaynağının hareketinin sonucu olarak birbirine yaklaşır. Sonuç olarak, A gözlemcisi tarafından ölçülen A’ dalga boyu, kaynağın dalga boyu A dan daha kısadır. Her bir titreşim esnasında, yani bir periyotluk zamanda, kaynak, v_kT = v_k/f uzaklığı kadar hareket eder ve dalga boyu bu miktar kadar kısalır. Bu nedenle, gözlenen A’ dalgaboyu

λ’ = λ – Δλ = λ – (V_k/f)

ile verilir. λ = v/f olduğundan, A gözlemcisi tarafından duyulan frekans

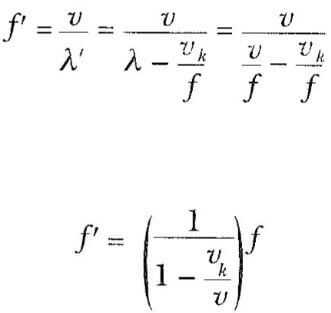
olur. Yani; gözlenen frekans, kaynak gözlemciye doğru hareket ettiği zaman artmaktadır.

Kaynak, Şekil 3a’da B gözlemcisi halinde olduğu gibi hareketsiz göz­lemciden uzaklaştığı zaman, gözlemci A ’dan daha büyük olan bir λ’ dalga bo­yu ölçer

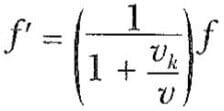
ile verilen azalan bir frekans işitir.

Eşitlik 4 ve Eşitlik 5, eşitliklerini birleştirirsek, kaynak hareketli, gözlemci hare­ketsiz olduğu zaman gözlenen frekans için genel bir bağıntıyı

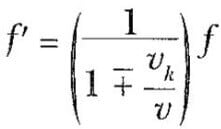
olarak ifade edebiliriz.Son olarak, kaynak ve gözlemcinin her ikisi hareketli ise, duyulan frekans için aşağıdaki genel bağıntıyı buluruz:

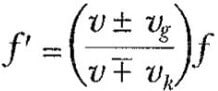
olur. Bu ifadede üstteki işaretler (+v_g ve -v_k) birbirine doğru harekete, alt işa­retler (-v_g ve +v_k) birbirinden uzaklaşan harekete karşılık gelir.

Doppler olayı problemleri ile çalışılırken, ilgili işaretleri hatırlamak için uygun kural aşağıdadır:

Birbirine doğru ifadesi, ölçülen frekansta bir artışı, birbirinden uzaklaşma ifade­si, ölçülen frekansta azalmayı gösterir.

Doppler olayı, tipik olarak ses dalgaları ile incelenmesine rağmen, tüm dalgalan kapsayan bir olgudur. Örneğin, kaynak ve gözlemcinin bağıl hareke­ti, ışık dalgalarında bir frekans kaymasına yol açar. Doppler olayı polis radar sistemlerinde motorlu araçların hızlarını ölçmek için kullanılır. Aynı şekilde astronomlar, yıldızların, galaksilerin ve diğer gök cisimlerinin yere göre bağıl hızlarını belirlemek için Doppler olayını kullanırlar.